Computational Environmental Heat Transfer
ISSN: 3068-5486 (Online)
Email: [email protected]


Heat transfer is the mechanism by which heat is transferred between different mediums or within a single medium, when they are at different temperatures. The means of heat transfer are categorized as: conduction, convection, and thermal radiation. A fluid with enhanced heat transfer characteristics can be devised by combining a base fluid with nanoparticles, named as a nanofluid. The dispersed nanoparticles and the used base fluid create distinctions between different nanofluids. Base fluid refers to the primary fluid in which nanoparticles are dispersed. It serves as a carrier fluid for nanoparticles. Frequently used base fluids are water, oil, ethylene glycol, etc. To get greater and enhanced heat transfer characteristics, we can transform nanofluids into a hybrid nanofluid by dispersing a suitable blend of multiple nanoparticles in the same primary fluid. It's very evident that in industrial and thermal management, nanofluids play a vital role in various fields, including industrial and technological applications. A permeable surface refers to a surface that allows water to penetrate through it. Such a surface facilitates water purification, promotes natural drainage, and refills groundwater. They have wide applications in driveways and sports fields. Thermal boundary slip refers to the odd behavior that occurs at the contact zone of the fluid and rigid surface. In comparison with bulk fluids, molecules exhibit distinct behavior near the boundary. This unusual behavior is visible when the slip length, which controls velocity and temperature gradient at the solid fluid interface, changes. This phenomenon is very essential in nanofluids and microfluids.
Clarke et al. [1] examined free convection for a horizontal porous heated surface. Variable gas properties were observed by assuming the fact that dynamic viscosity and thermal conductivity were relational to temperature. Schlichting et al. [2] analyzed the boundary equations for turbulent and laminar flows. Flow around circular cylinders and stagnation point flow were also observed. Roganov et al. [3] discussed various features and characteristics of turbulent heat transfer at permeable surfaces. The modelling for a relation between pressure and temperature was underscored. Chaudhary et al. [4] employed similarity solutions to solve the model for free convective fluid flow along permeable erect surfaces immersed in porous material. It was observed that solutions were reliant on two dimensionless parameters, namely the mass transfer parameter and power law exponent. A novel class of fluid named as hybrid nanofluid was explored for enhanced heat transfer characteristics by Eastman [5]. It was observed that even a small proportion of nanoparticles in the fluid turned out with better heat transmission characteristics of the fluid. Hussain et al. [6] considered buoyancy-driven heat and mass transport from an upright permeable smooth plate having a non-constant temperature. Four variant approaches were employed to get the numerical solution of governing equations, including the perturbation method, asymptotic solutions, Keller-box method, and local non-similarity approach. The transition of heat transfer from enhancement to reduction for different aspect ratios was examined by Yu et al. [7]. They considered laminar flow for rectangular micro channels and used the integral transform technique to resolve the energy equation. Results were tabulated in terms of local and mean Nusselt numbers. Ali et al. [8] studied laminar free-forced convection flow that arises due to the continuous stretching of the permeable surface. It was observed that the buoyancy force had no impact on the surface due to the reverse correlation between temperature and distance above the surface. The partial slip flow of a Newtonian fluid across a stretchable sheet was considered by Andersson et al. [9]. The numeric values of non-dimensional slip factor, from zero to infinity, were used to control partial slip.
Khanafer et al. [10] examined the augmentation in free convection heat flow by taking into account the nanofluids. The model was developed and solved numerically by employing the Finite volume technique. Later on, Maiga et al. [11] extended it for forced convection heat transient for two different geometries. A slip boundary condition was used by Martin et al. [12] to evaluate laminar flow over a plate. It was observed that slip condition dropped down the global drag force, but two-dimensional effects locally increased the skin friction. With the consideration of partial slip, Ariel et al. [13] interpreted the flow characteristics of elastic-viscous fluid over a stretching membrane. They further discussed their findings about the impact of partial slip on the skin friction coefficient and velocity profile. Berg et al. [14] extended the investigation of fluid behavior in porous medium to the two-phase flow by considering the slip boundary condition. It was further observed that the radius of flow channels determines the enhancement in flux due to slip. Abu-Nada et al. [15] utilized nanofluids to boost the heat transfer in horizontal annuli. Moreover, the effect of nanoparticles, with low and high thermal conductivity, on heat transfer characteristics was observed. Ishak et al. [16] considered a mobile porous flat membrane in a parallel stream to examine transpiration impacts over the flow. By keeping the above conditions in view, a respective model is developed and solved by using the finite difference method. Martin et al. [17] allowed a slip boundary condition over a wedge by considering the modified Falkner-Skan solution for streamline flow. A remarkable decrease in skin friction, velocity, and temperature boundary layer thickness is noticed due to the inclusion of a slip boundary condition. Ishak [18] considered a flat permeable surface whose bottom is heated with the hot fluid through convection. It was noticed that the thermal transfer rate escalates due to suction. Abu-Nada et al. [19] focused on the impacts of varying thermal conductivity and fluctuating viscosity of nanofluids, -water and CuO-water on free convection heat transfer in enclosures.
Aziz [20] took into consideration a uniformly heated flat plate under the influence of thermal slip flow. It was observed that the slip parameter relates directly to slip velocity and inversely to wall shear stress. Temperature variant viscosity and thermal conductivity of micro polar fluid for an inclined permeable wall were investigated by Rahman et al. [21]. It was noted that an increase in the thermal conductivity parameter upturned the velocity and temperature of the boundary layer. Impact of thermal radiation on a magnetically influenced upstanding plate was investigated by Ashraf et al. [22] for free-forced convection. Effects of dimensionless parameters were observed graphically and in tabular form against the skin friction coefficient and the transpiration parameter. Buoyancy-driven flow in a cavity, whose lateral walls were thermally active, was computationally studied by Sheikhzadeh et al. [23]. The enclosure was occupied by Cu water nanofluids. It was concluded that there is an escalation in the average Nusselt number with the rise in Rayleigh number and volume fraction of dispersed nanoparticles. Accounting for the effects of Brownian motion and thermophoresis, Khan et al. [24] numerically explored the buoyancy-driven flow over an erect plate having constant heat flux. The transport mass and energy equations were further analyzed by using similarity transformations. Subjected to a transverse magnetic force field, Su et al. [25] investigated Falkner-Skan flow in the boundary layer region above a permeable plate. A comparison was made between the approximate and numerical solutions, and found that they were in good agreement. Suresh et al. [26] examined the influence of water-based hybrid nanofluid in heat transfer for uniformly heated circular tubes. It was perceived that an enhancement in the convective heat transfer coefficient causes an increase in the Reynolds number. Under the action of radiant energy and temperature-dependent heat transmission, Cortell [27] examined heat transfer characteristics for an incompressible fluid above a stretching penetrable interface within a porous material. Moreover, the consequences of Pr, fluctuating thermal conductivity, permeability, and thermal radiation on the rate of heat transfer were plotted graphically and also presented in tabular form. Alvarino et al. [28] explored the implications of molecular and thermal diffusion in the entrance area of a tube for convective heat transfer in hybrid nanofluids. Ashraf et al. [29] studied the cumulative impact of radiation-conduction and hydro magnetics for electrically conducting fluid across a magnetized perpendicular permeable plate. Finite difference technique was adopted to compute the numeric solution of equations. Huminic and Huminic [30] summarized significant work of many researchers related to the effectiveness of nanofluids in the augmentation of convectional heat transfer in heat exchangers. Heat conduction and viscosity of nanofluids were also discoursed theoretically and experimentally. Noghrehabadi et al. [31] reported the impact of partial slip over a stretching surface for boundary layer flow influenced with nanoparticles. A strong impact of the slip parameter over the flow velocity and shear stress of the stretching sheet was observed. Ibrahim et al. [32] explored boundary layer flow for a stretching permeable sheet. An enhancement in sheet temperature was observed due to an increase in values of the Echert number. Runge Runge-Kutta approach was applied to numerically integrate the equations. Labib et al. [33] inspected the influence of conventional fluids on convective heat transfer mixed with nanoparticles, by using two distinct base fluids. It was noticed that ethylene glycol proved more beneficial for enhanced heat transfer as compared to water. Four distinct nanoparticles along with water as carrier the fluid were considered by Abolbashari et al. [34] to examine MHD flow for stretching a permeable surface. Homotopy perturbation method was implemented to resolve fundamental equations. Also, the impact of thermophysical parameters was observed graphically. The benefits of using porous medium impacted by nanofluid were discussed by Mahdi et al. [35]. It was noted that as compared to conventional fins, the dissipation area of porous medium was much greater, which resulted in the amplification of heat transfer characteristics.
In view of the limited understanding of nanofluid heat transfer mechanisms, Sarkar et al. [36] apprehend the advantages and suitable applications of hybrid nanofluids in heat transient enhancement and pressure gradient attributes, respectively. Later, Sidik et al. [37] apprehend the production of hybrid nanoparticles and hybrid nanofluid, and also their effectiveness in thermal energy transient. The future challenges related to the application of hybrid nanofluids have also been discussed. Aluminum nitride nanoparticles were distributed in ethylene glycol, which served as a base fluid, by Hussein et al. [38] to escalate the heat transient mechanism within a dual-tube heat exchanger. It was found that the thermal performance of the heat exchanger was more promising for composite nanofluids in relation to traditional fluids. Kasaeian et al. [39] reported thermal transport traits of nanofluid for porous medium. It was observed that the combined effect of porous media and nanofluid augmented heat transfer in a heat exchanger. The problem of MHD flow for permeable walls of a channel was researched by Fakour et al. [40]. The least squares method was executed to solve the resulted differential equations of higher order. The outcomes were contrasted with the one already presented in the literature to examine their validity. Sundar et al. [41] pointed out the drawbacks of using a hybrid nanofluid. It was explored that the higher the heat transfer rate, the higher the viscosity of the fluid. The impact of platinum hybrid nanofluid over heat flux was observed by Yarmand et al. [42]. It was witnessed that the elevation in the Nusselt number relied upon the values of the Reynolds number. Bhattad et al. [43] numerically and experimentally explored the impact of hybrid nanofluid on pressure variance and heat transfer efficiency of a plate heat exchanger. Velocity and thermal boundary layer profiles have been established for base fluid, nanofluids, and nanostructured fluid. Minea et al. [44] compared traditional fluids with hybrid nanofluids in terms of heat transfer characteristics. It was reported that a synergistic effect, leading to long-term stability, can be obtained by fusion of appropriate nanoparticles in a base fluid.
The role of nanofluid and hybrid nanofluid in thermal conductivity for the shrinking sheet was observed by Aly et al. [45]. In relation to nanofluid, hybrid nanofluid proved more fruitful for heat transfer in the case of a shrinking sheet. Kumar et al. [46] investigated the impact of nonlinear radiant energy and a continuously varying heat source and sink on a micropolar fluid flow above a stretching surface by considering a second-order slip condition. Appropriate similarity variables were used to transform PDEs into ODEs. It was predicted that the velocity distribution would be strengthened and the temperature distribution would be reduced due to second-order slip. Sidik et al. [47] assessed the methods of synthesizing hybrid nanofluids and the factors affecting their performance. It was further predicted that hybrid nanofluids work very effectively as a substitute for the convective coolants working at higher temperatures. In [48], the existing facts about hybrid nanofluids and the challenges and difficulties faced by the fresh researchers were discussed in detail. It was further advised that, regardless of the attractive and effective characteristics of hybrid nanofluids, a lot of devotion is needed in the development, implementation, and stability of models, helpful in simulating the thermodynamic pattern and heat transient features. Effectiveness of the Lorentz force and irregular viscosity in the augmentation of heat transfer, with the influence of nanoparticles-based hybrid fluid, was considered by Manjunatha et al. [49]. Ashraf et al. [50] studied boundary layer flow of nanofluids at distinct positions on a sphere under free convection conditions. It was observed that the concentration of nanoparticles was minimum at site , but maximum at respectively. Shafiq et al. [51] examined three-dimensional rotating frame influenced with thermal boundary slip for nanofluid flow. The prominent feature of this work was Arrhenius activation energy. It was observed that elevation in stretching values resulted in a reduction of fluid velocity.
A permeable elastic sheet was considered by Roy et al. [52] to investigate thermal aspects of a second-grade nanofluid mixture. It was seen that the suction parameter is related directly to fluid velocity and inversely to temperature. Waini et al. [53] studied MHD flow over a shrinking permeable wedge for a hybrid nanofluid. MATLAB was leveraged to optimize the primary equations numerically. It was concluded that an increase in the radiation parameter caused a decrease in the rate of heat transfer. Jeelani et al. [54] examined non non-Newtonian Maxwell model in which ethylene glycol served as a base fluid with the dispersion of alumina and copper nanoparticles to investigate heat transfer enhancement. A numerical solver, bvp4c, is utilized to obtain a solution of the underlying equations. Bhattad et al. [55] reviewed preparation techniques and implications of mono-nanofluid and nanofluid mixtures. Their characteristics as a working fluid were also underscored.
In view of previous studies, this dissertation aims at the enrichment of mixed convective heat transfer in the close neighborhood of a permeable vertical surface with the inclusion of thermal boundary slip. The variations in the flow structure, including velocity and thermal boundary layer profiles, will be analyzed.
A dual dimensional steady, viscous flow of hybrid nanofluid alongside a permeable vertical plate is considered in Figure 1. The surface lies in direction while -axis is at right angle to it. The thermo-physical specifications of the fluid are considered invariable, where the viscosity and density are considered to be of the hybrid nanofluid. To merge the impact of thermal boundary slip, adjustments are made in the respective boundary conditions of the model.
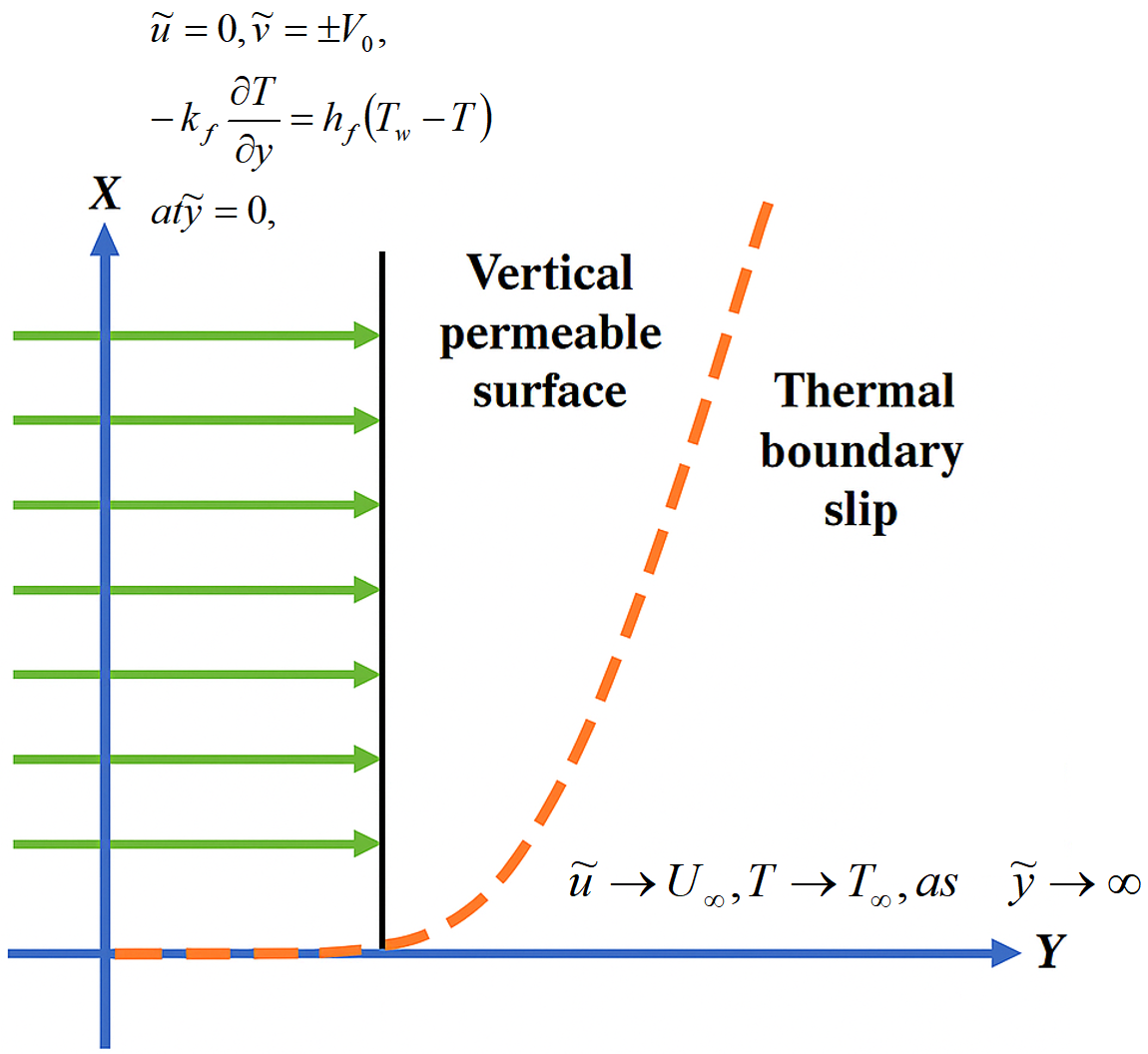
In reliance on the above premises and by following [29] and [54], the boundary layer coupled mass, momentum, and energy equations are formulated as:
where and are the horizontal and normal components of velocity, respectively. indicate fluid's consistency, fluid's concentration, thermal expansion coefficient, thermal transport coefficient, and volumetric heat capacity of hybrid nanofluid, respectively. refers to the temperature of the fluid.
The associated boundary conditions (by following [51]) are:
where is the thermal conductivity of the fluid and is the heat transfer coefficient.
Dimensional analysis is a process employed on equations to combine distinct physical quantities in such a way that the dimensions of the quantities get canceled out. The originated unit-less quantities help to describe the behavior of fluid independent of units. It is used to analyze the system behavior and explore the dominant physical controlling factor of the system.
To obtain dimensionless boundary layer equations and respective interface conditions, we are going to introduce the following scale-invariant parameters.
By substituting (5) in equations (1) – (4), the obtained dimensionless model is stated as
where and correspond to the normalized velocity components along and directions, respectively. Moreover, , , and Pr represent the non-dimensional fluid temperature, mixed convection parameter, and Prandtl number, respectively.
The respective dimensionless boundary conditions are given as:
where is transpiration parameter and is thermal slip parameter.
The finite difference method is a numerical approach employed to get the solution of differential equations. It is an approximation technique centered on discretization. It helps to simplify problems, which facilitates effective handling of complex geometries.
To employ this technique, primarily, the primitive variables are introduced.
For convenient integration of the obtained dimensionless model, the following parameters are introduced:
By substituting (10) in boundary layer equations (6) – (8), the mass conservation, energy, and motion equations are transformed into:
The transformed boundary conditions can be written as:
With the help of following central difference and backward difference along and direction respectively, we will discretize the equations (11) – (13)
Similarly for ,
By using the above equations (15) and (16) and simplifying the terms, we get the following velocity component from the continuity equation, which can be used to determine the velocity of the fluid.
The discretized version of the momentum transport equation is
where
And the discretized representation of the energy balance equation is:
where,
The discretized boundary conditions are:
The values of physical properties of hybrid nanofluid used in above equations are stated (by following [54]) as:
where and represent the volume fractions of solid nanoparticles, and and denote the thermophysical characteristics of two different types of nanoparticles.
|
Base fluid (air) | Al2O3 | Cu | |||
|---|---|---|---|---|---|---|
| (Kg/m3) | 1.225 | 3970.0 | 8933 | |||
| (JKg-1K-1) | 1007 | 765.0 | 385.0 | |||
| (Wm-1K-1) | 0.0255 | 40.0 | 400.0 |
| Skin friction | Heat transfer rate | |
|---|---|---|
| 0.1 | 31.75944 | 0.34833 |
| 0.71 | 22.4168 | 0.73371 |
| 3.0 | 16.78128 | 1.16082 |
| 5.0 | 15.06431 | 1.34858 |
| 7.0 | 14.00757 | 1.48491 |
| 10.0 | 12.94953 | 1.64171 |
| Skin friction | Heat transfer rate | |
|---|---|---|
| 0.01 | 0.40151 | 0.80025 |
| 0.03 | 0.41002 | 0.80106 |
| 0.05 | 0.41094 | 0.80157 |
| 0.07 | 0.41171 | 0.80295 |
| 0.09 | 0.41221 | 0.80302 |
| 0.10 | 0.41260 | 0.80309 |
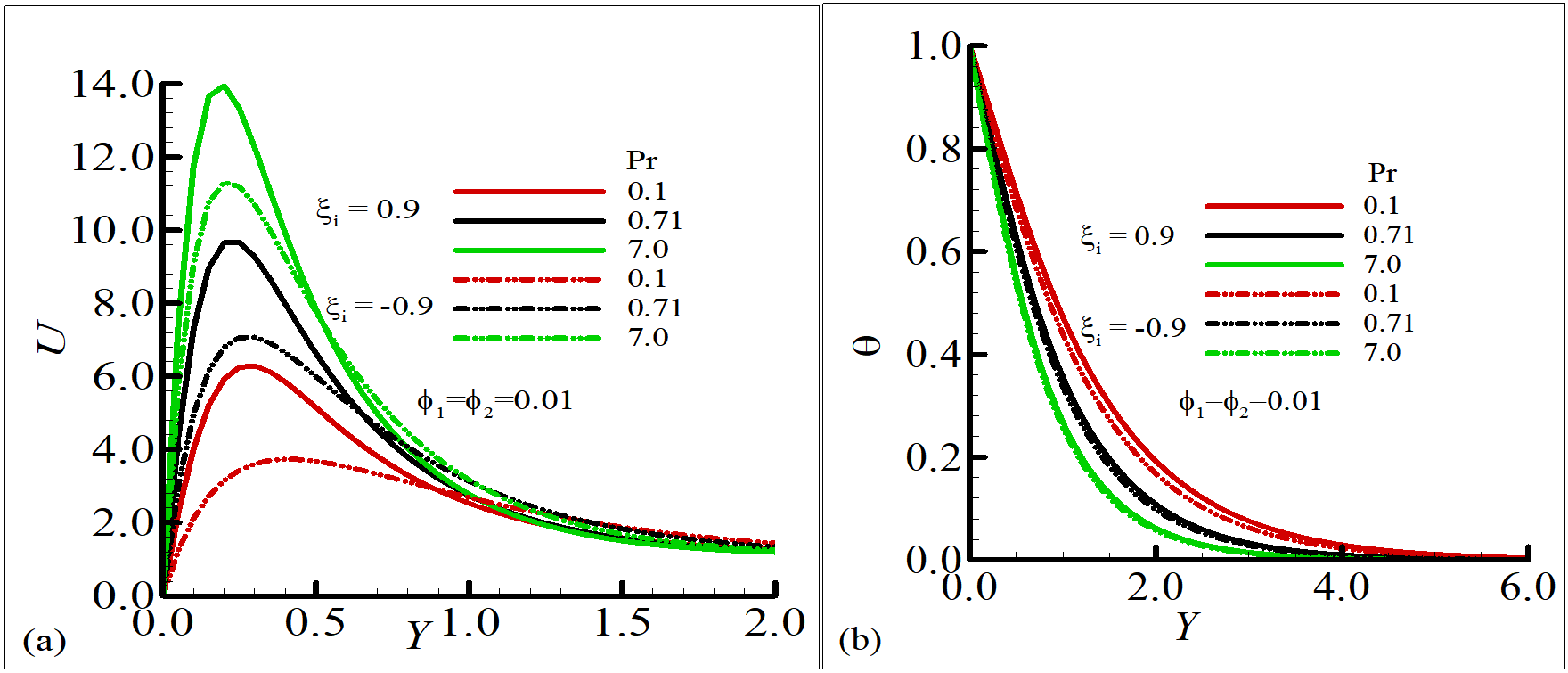
This portion illustrates the impact of the dimensionless parameter Prandtl number (Pr) and the transpiration parameter () on the velocity and temperature profiles. This parametric analysis of velocity and temperature facilitates a better understanding of the fluid pattern. The relevant physical properties are summarized in Table 1.
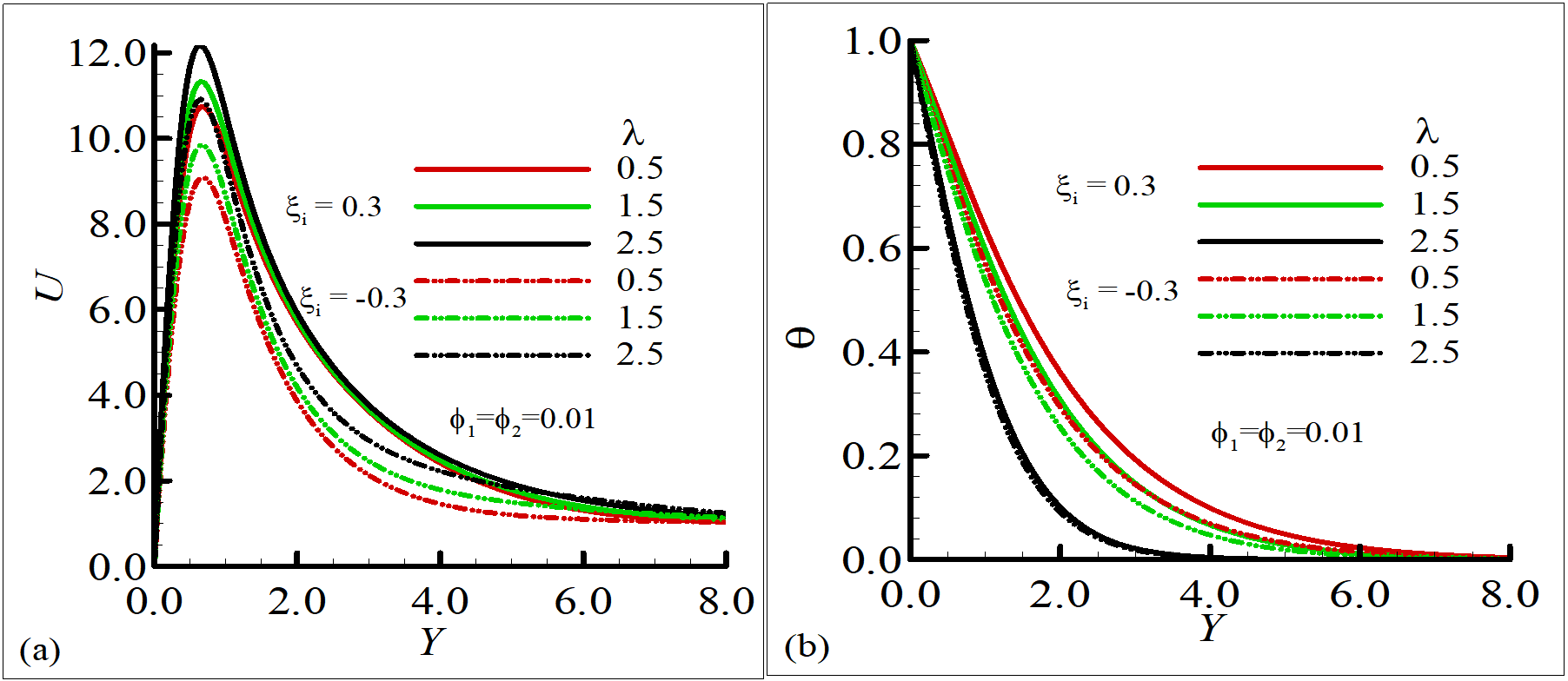
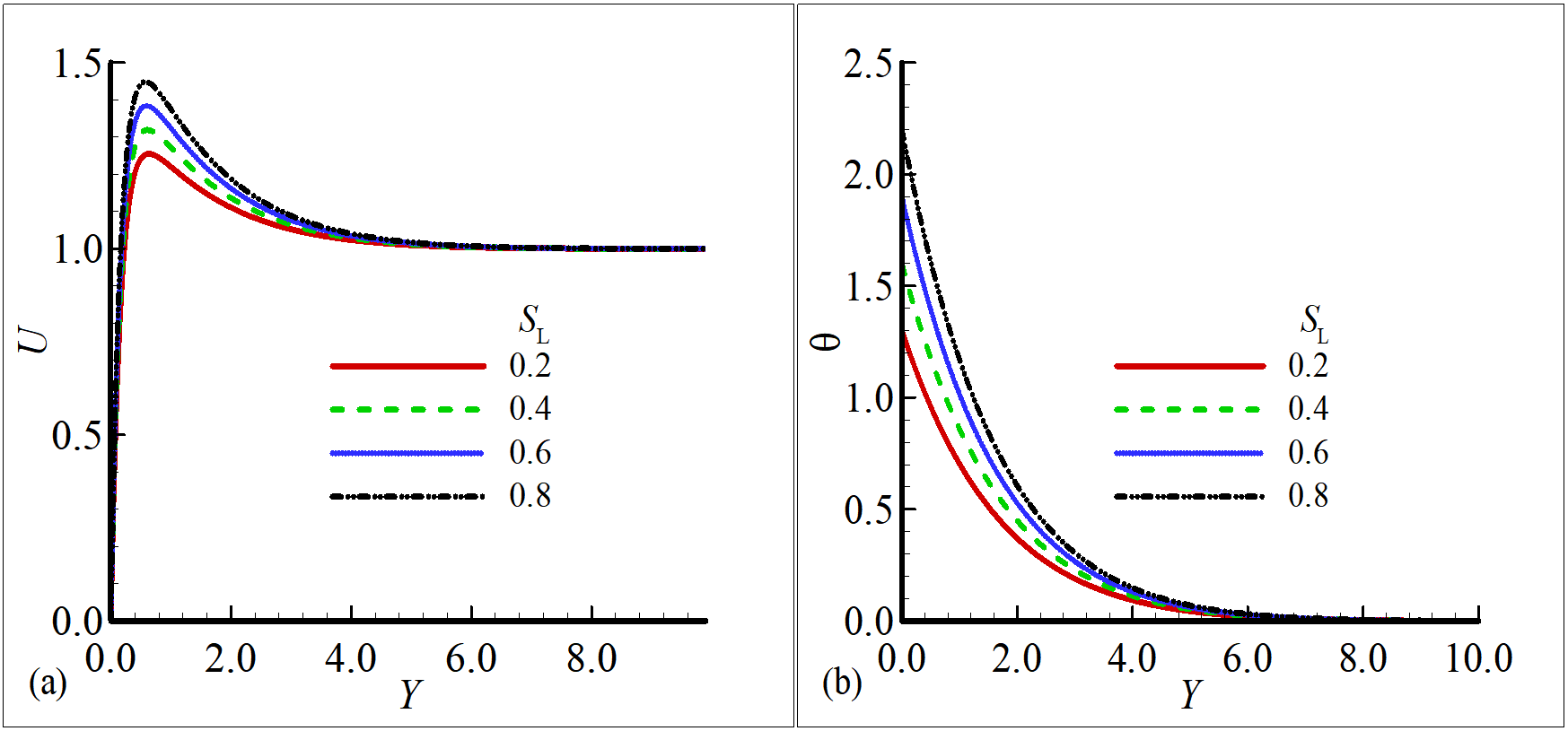
Table 2 depicts the impact of Pr on the frictional drag force and the rate of heat exchange. It is observed from the table that a rise in the magnitude of the Prandtl number decays the frictional resistance. Since a high value of the Prandtl number increases the thickness of the fluid, which decelerates the flowing fluid, leading to the enhancement in the skin friction coefficient . However, this effect of viscosity is encountered by the inclusion of thermal boundary slip. The velocity of the fluid drops due to thermal boundary slip, which in turn reduces the magnitude of skin friction. In the opposite vein, the higher the value of the Prandtl number, the higher is the rate of heat transfer. Since the inclusion of thermal boundary slip decreases the thickness of the thermal boundary layer and develops a temperature gradient in proximity to the surface, it leads to improved heat flux. For , fluid's viscosity is dominated by thermal diffusivity, which elevates heat flux by reducing the frictional force of the fluid.
The impact of the transpiration parameter against skin friction coefficient and thermal flux can be observed from Table 3. It is noted that the transpiration parameter relates directly to the frictional factor and heat transmission rate. Due to the increased value of the transpiration parameter and inclusion of thermal boundary slip, permeability improves. This improved permeability of the surface helps the fluid to get more stabilized and facilitates easy fluid flow through the surface, resulting in enhanced heat transmission characteristics of the fluid. Also, suction reduces the boundary layer thickness of fluid, facilitating more contact between the surface and the flowing fluid. This enhanced contact increases the skin friction coefficient.
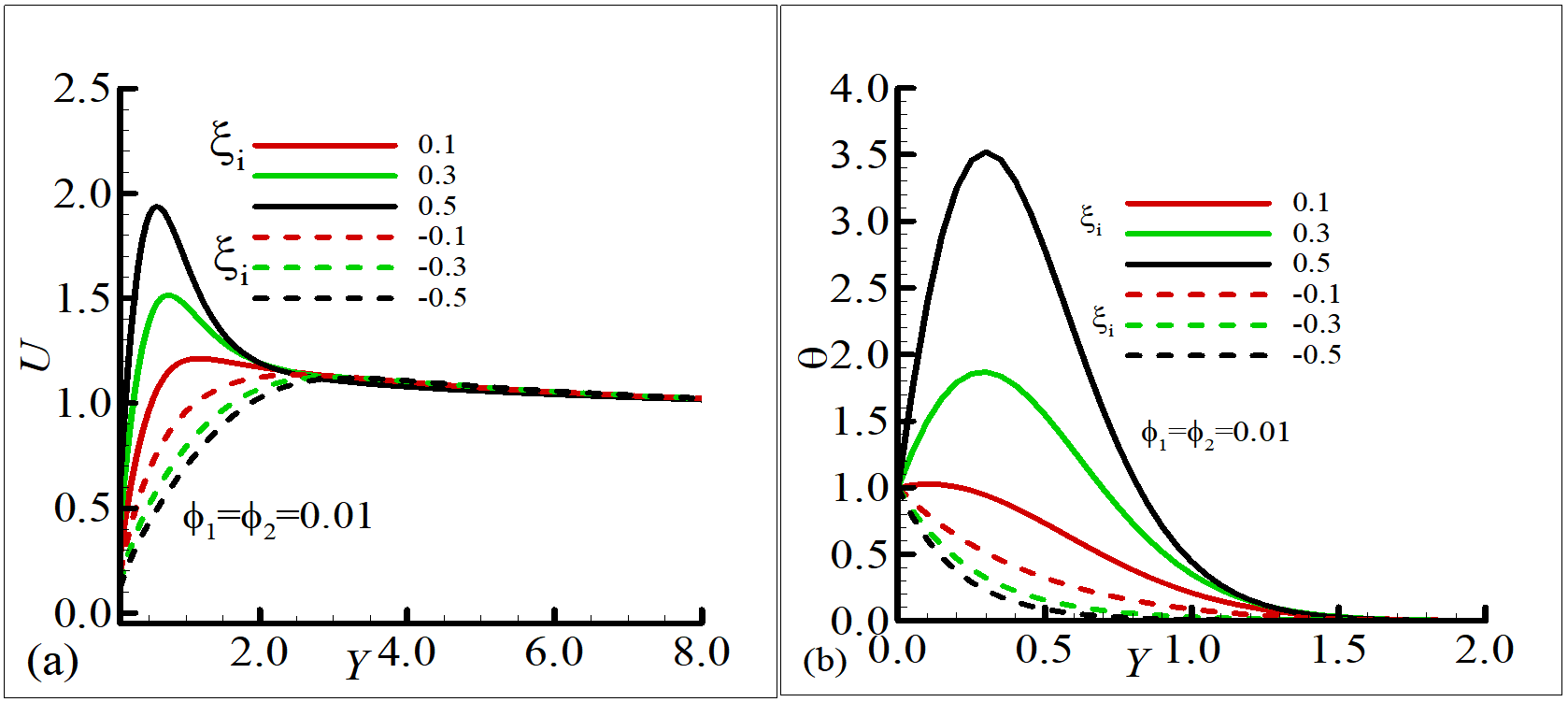
Figure 2 portrays how the transpiration parameter influences the fluid's velocity and temperature distribution , revealing that with thermal boundary slip considered, suction enhances both velocity and temperature at the surface, while maintaining a constant profile away from it. This occurs because suction is enhanced by the incorporation of thermal slip condition, which reduces the boundary layer thickness, facilitates smoother flow, and improves thermal distribution. In the same manner, increasing values of injection accelerate the fluid and temperature of the fluid due to the significant presence of thermal boundary slip.
Figure 3 characterize the impact of Prandtl number Pr in opposition to fluid velocity and temperature where and . It illustrates that for both suction and injection, an elevation in the numeric data of Pr results in the rise of velocity of fluid and a downfall of temperature adjacent to the surface. It shows that for distinct values of Prandtl number, different fluids (water, air, and oil) behave in a similar way for suction and injection.
The impact of mixed convection parameter on the temperature and velocity of the fluid is depicted by Figure 4. It is witnessed that elevated values of the mixed convection variable boost the velocity and reduce the temperature of the fluid. Since, for higher values of , buoyancy flow dominates the forced flow, causing an increase in fluid velocity, and a uniform temperature distribution reduces the temperature of the fluid.
It is observed from Figure 5 that augmentation in slip parameter lessens the boundary layer thickness by improving permeability, which permits fluid to flow faster. As a result, it increases the velocity of the fluid. Since a high value of the slip parameter facilitates fluid flow, it also results in effective thermal characteristics of the fluid.
The above study underscores the characteristics of heat transfer for hybrid nanofluid adjacent to a vertical permeable surface influenced by thermal boundary slip. It highlights the impacts of Prandtl number (Pr) and transpiration parameter () against the rate of heat transfer , temperature (), skin friction coefficient (), and velocity () of the fluid numerically and graphically.
Our analysis shows that:
Boosting the value of the Prandtl number (Pr) minimized the frictional drag coefficient and elevated the rate of heat transport.
With the augmentation in the transpiration parameter, a gradual increase in the thermal flux and frictional coefficient is observed.
An enhancement in the transpiration parameter results in escalated velocity and fluid temperature due to suction.
It is also noted that elevated values of injection accelerate the velocity and thermal characteristics of a fluid. For a diverse range of Prandtl numbers (), distinct fluids (water, air, and oil) showed the same pattern.
| Roman Letters | ||
| Coordinate adjacent to the surface | ||
| Coordinate normal to the surface | ||
| Vertical velocity component | ||
| Horizontal velocity component | ||
| Temperature of fluid | ||
| Temperature of permeable surface | ||
| Free stream temperature | ||
| Non-dimensional vertical velocity component | ||
| Non-dimensional horizontal velocity component | ||
| Ambient fluid velocity | ||
| Fluid-specific heat | ||
| Conduction coefficient of fluid | ||
| Conduction coefficient of base fluid | ||
| Conduction coefficient of hybrid nanofluid | ||
| Permeability of the surface | ||
| Re | Reynolds number | |
| Pr | Prandtl number | |
| Greek Letters | ||
| Thermal diffusivity | ||
| Dimensionless transpiration parameter | ||
| Primitive non-dimensional temperature | ||
| Kinematic viscosity of the fluid | ||
| Fluid's dynamic viscosity | ||
| Density of the fluid | ||
| Free stream density | ||
| Volumetric expansion coefficient (hybrid nanofluid) | ||
| Kinematic viscosity of hybrid nanofluid | ||
| Dynamic viscosity of hybrid nanofluid | ||
| Density of the hybrid nanofluid | ||
 Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. 
Portico
All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/