1. Introduction

How to represent and measure the uncertainty is one of the central issues in information sciences. In general, the uncertainty can be briefly classified into random uncertainty and epistemic uncertainty [33]. Attributed to Shannon's innovative contributions [1], quantifying the randomness of uncertain information is solved through the mathematical framework of information theory. Dempster-Shafer theory [2, 3], also known as belief function theory, is a widely used framework to represent information with epistemic uncertainty, where a mathematical structure called mass functions is provided to simultaneously describe discord and non-specificity involved in the given information [4]. However, measuring the uncertainty of mass functions is not yet well solved currently, especially it still has not a consensus with respect to the definitions of entropy, cross entropy, and relative entropy of mass functions.

With respect to the entropy of mass functions, many researchers have paid attention on the problem [5, 6, 7]. Klir [8] has proposed generalized information theory (GIT) which aims to generalize Shannon's information theory for probabilities to various uncertainty theories including imprecise probabilities, fuzzy sets, belief functions, and so on. However, the proposed aggregated uncertainty (AU) in GIT for mass functions is of some shortcomings [9], especially some of the underlying axiomatic requirements of AU have been challenged [10]. Recent years, with the proposal of Deng's entropy [11], a new entropy measure for calculating the uncertainty of a mass function, the research of uncertainty measures in Dempster-Shafer theory has welcomed a "strong resurgence" [12]. Many novel entropy definitions of mass functions have been put forward [13, 14, 15]. For example, Jirousek and Shenoy [10] designed an entropy measure for mass functions by combining plausibility transformation and weighted Hartley entropy. Zhou and Deng [16] proposed a fractal-based belief entropy on the basis of Deng's entropy. In terms of belief intervals of single elements, Moral-Garcia and Abellan [17] developed an uncertainty measure of mass functions which is analogous to AU. Besides, Cui and Deng [18] presented a total uncertainty measure of mass functions based on plausibility function, which is called plausibility entropy. Facing existing uncertainty measures, Dezert and Tchamova [19] have raised the effectiveness problem of uncertainty measures, and provided four desiderata to check if an uncertainty measure is effective, and a new effective measure of uncertainty for mass functions has been proposed in [20].

Cross entropy and relative entropy are another two important concepts according to Shannon's information theory. Although the research of entropy of mass functions is flourishing, cross entropy and relative entropy of mass functions, however, are relatively rare. This matter of fact is easy to understand, because cross and relative entropies are strongly connected with the concept of entropy, their forms are usually on the basis of the definition of entropy. Many existing entropy measures of mass functions are hard to yield corresponding cross and relative entropies. Very recently, Dezert and Dambreville [21] have provided definitions of cross entropy and relative entropy of mass functions in terms of Dezert's effective measure of uncertainty presented in [20]. In addition, Gao et al. [22] proposed a definition of cross entropy of mass functions based on Deng's entropy [11]. However, as will be analyzed in this paper, the existing definitions of cross entropy of mass functions are of some defects in underlying properties, new cross entropy, as well as corresponding relative entropy, of mass functions are required, which is the purpose of the study.

Specifically, inspired by the plausibility entropy, a total uncertainty measure of mass functions, presented in [18], new cross entropy and relative entropy of mass functions are given in this paper, which are named as cross plausibility entropy and relative plausibility entropy, respectively. The properties of cross and relative plausibility entropies are given, which shows a strong connection with classical cross entropy and relative entropy in Shannon's information theory. In addition, an illustrative example in parameter estimation is given to show the potential application of the presented entropies.

The remainder of the paper is organized as follows. Section 2 briefly introduces the basic knowledge of Dempster-Shafer theory. Related work regarding existing definitions of cross entropy of mass functions are reviewed in Section 3. Then, new cross and relative entropies of mass functions are given in Section 4. An example of application is provided in Section 5. Finally, Section 6 concludes the study.

2. Basics of Dempster-Shafer theory

Dempster-Shafer theory [2, 3] has provided a well-defined framework to represent and deal with uncertainty information with epistemic uncertainty. In this theory, the set of possible answers to a given question of interest is called as a frame of discernment (FOD), denoted as $\Omega =\{{\theta }_1,{\theta }_2,\cdots ,{\theta }_n\}$, in which the set is collectively exhaustive and all elements in a FOD are mutually exclusive. The power set of FOD $\Omega$ is represented by $2^{\Omega }$.

In order to represent the uncertain information involving epistemic uncertainty, mass functions, also known as basic probability assignments (BPAs), are defined in Dempster-Shafer theory. A mass function is a mapping from the power set of a FOD to interval $[0,1]$, denoted as $m:2^{\Omega }\to [0,1]$, satisfying the following conditions

where $A$ is called as a focal element of $m$ if $m\left(A\right)>0$, and $m\left(A\right)$ measures the belief assigned exactly to $A$. In general, a probability distribution can be treated as a Bayesian mass function in Dempster-Shafer theory, where $\forall A$ with $\left|A\right|\ge 2$ there is $m\left(A\right)=0$.

Belief function $Bel$ and plausibility function $Pl$ are two equivalent forms of mass functions, which respectively express the lower bound and upper bound of the support degree of a set $A$ based on a given mass function $m$, $A\subseteq \Omega$. Given a mass function $m$, $Bel$ and $Pl$ are defined as follows

where $\overline{A}=\Omega -A$. For each $A\subseteq \Omega$, there is $Bel\left(A\right)\le Pl\left(A\right)$, and $[Bel\left(A\right),Pl\left(A\right)]$ is called the belief interval of $A$. In general, the wider the belief interval of a set $A$, the larger the uncertainty it contributes to the whole mass function. Therefore, in Dempster-Shafer theory, given a FOD $\Omega$, the vacuous mass function $m_{\gamma }$, in which $m_{\gamma }\left(\Omega \right)=1$, has the largest uncertainty.

3. Related work

In this section, two existing definitions of cross entropy of mass functions, proposed very recently, are reviewed.

4. New cross and relative entropies of mass functions

5. An example of application

In this section, an illustrative example regarding parameter estimation is provided to show the potential application of proposed cross plausibility entropy $H_{Pl}(m_1,m_2)$. The example is originally from literature [28].

Assuming there are $n$ patients randomly taken from a population which has a proportion $\theta$ to suffer from a disease, and each of them is represented by $X_i$ to show if he/she has the disease (i.e., $X_i=1$) or not (i.e., $X_i=0$). Then, these random samples $𝐗=(X_1,X_2,\cdots ,X_n)$, which are independent and identically distributed (iid), can be viewed as the outcome of a Bernoulli variable. For realizations $𝐱=(x_1,x_2,\cdots ,x_n)\in {\Omega }_{𝐗}={\{0,1\}}^n$, the probability can be calculated by

The task is to estimate the unknown parameter $\theta$ according to state descriptions $𝐱=(x_1,x_2,\cdots ,x_n)$. However, due to the uncertainty, these states are only partially known, and let $m_i$ be the mass function concerning the state $x_i$ associated with patient $i$. Table 1 gives a data set composed of $n=6$ observations, in which the fourth one $m_4$ is uncertain and represented by $m_4\left(\left\{1\right\}\right)=\alpha$, $m_4\left(\left\{0\right\}\right)=\beta$, and $m_4\left(\{1,0\}\right)=1-\alpha -\beta$, where $\alpha ,\beta ,1-\alpha -\beta \in [0,1]$.

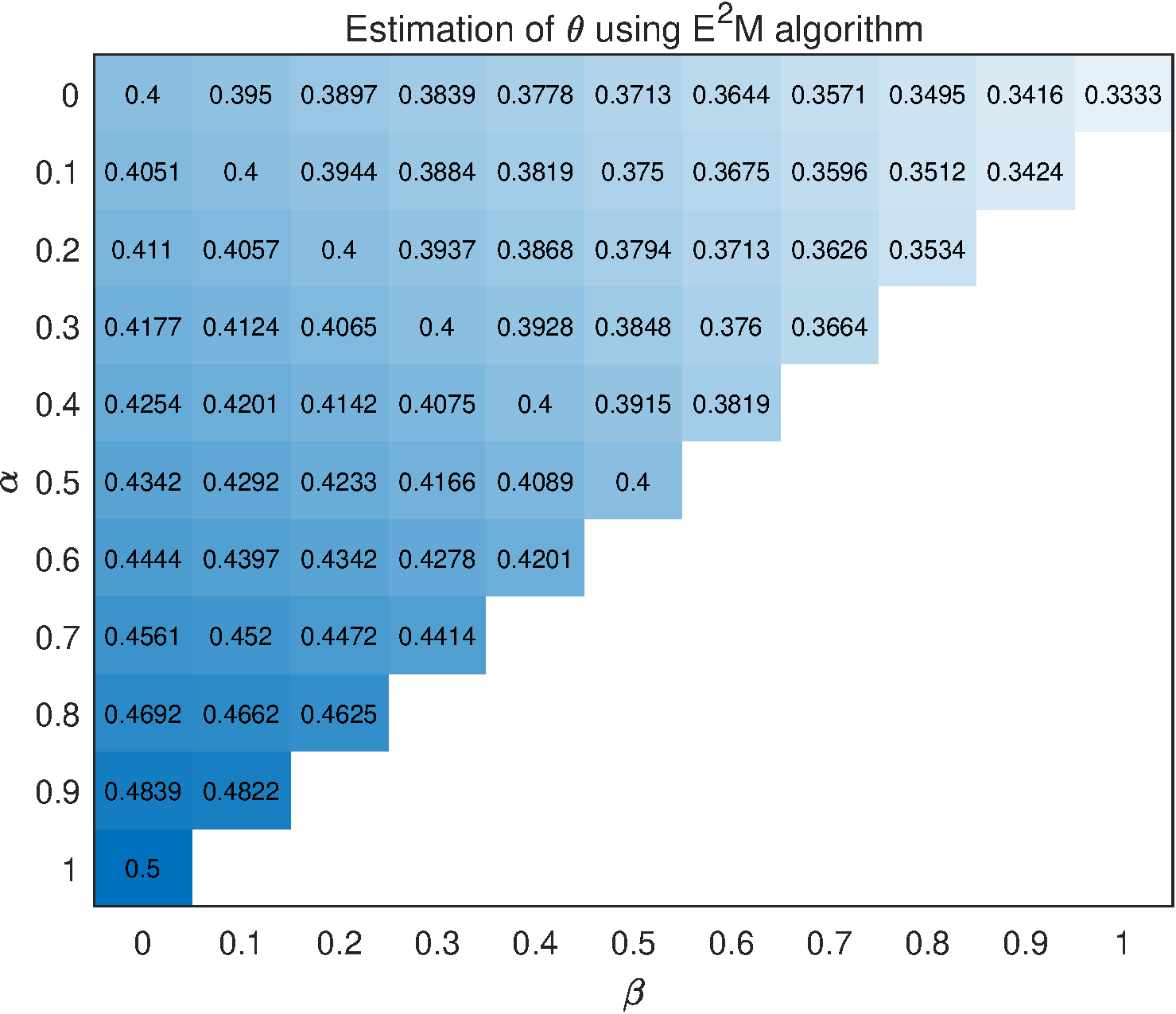
Literature [28] proposed an evidential expectation-maximization ($E^{2}M$) algorithm to estimate the parameter $\theta$, in terms of a maximum likelihood principle. Figure 1 gives the results of using $E^{2}M$ algorithm with respect to different $\alpha$ and $\beta$. It is found that, by using the $E^{2}M$ algorithm, the result of estimated $\theta$ is unchanged if the plausibility transformations of different $m_4$ caused by changed $\alpha$ and $\beta$ are the same. For example, let $m_4^1$ and $m_4^2$ be $m_4^1\left(\left\{1\right\}\right)=0.6$, $m_4^1\left(\left\{0\right\}\right)=0.4$, $m_4^1\left(\{1,0\}\right)=0$, and $m_4^2\left(\left\{1\right\}\right)=0.4$, $m_4^2\left(\left\{0\right\}\right)=0.1$, $m_4^2\left(\{1,0\}\right)=0.5$, respectively. There are $Pl\_P_{m_4^1}\left(\left\{1\right\}\right)=Pl\_P_{m_4^2}\left(\left\{1\right\}\right)=0.6$ and $Pl\_P_{m_4^1}\left(\left\{0\right\}\right)=Pl\_P_{m_4^2}\left(\left\{0\right\}\right)=0.4$, i.e., $Pl\_P_{m_4^1}=Pl\_P_{m_4^2}$. Then, by using the $E^{2}M$ algorithm, parameter $\theta$ is estimated as ${\theta }^{1,\ast }=0.4201$ associated with $m_4^1$ and ${\theta }^{2,\ast }=0.4201$ associated with $m_4^2$. Two observations with different uncertainty degrees, $m_4^1$ and $m_4^2$, lead to the same estimation of $\theta$.

Figure 1 Estimation of $\theta$ with the use of $E^{2}M$ algorithm by considering different values of $\alpha$ and $\beta$.

Now, let us use a cross entropy-based method to solve the issue of estimating parameter $\theta$, where $\theta$ is derived by minimizing a total cross entropy loss, which coincides with the maximum likelihood principle widely used in machine learning.

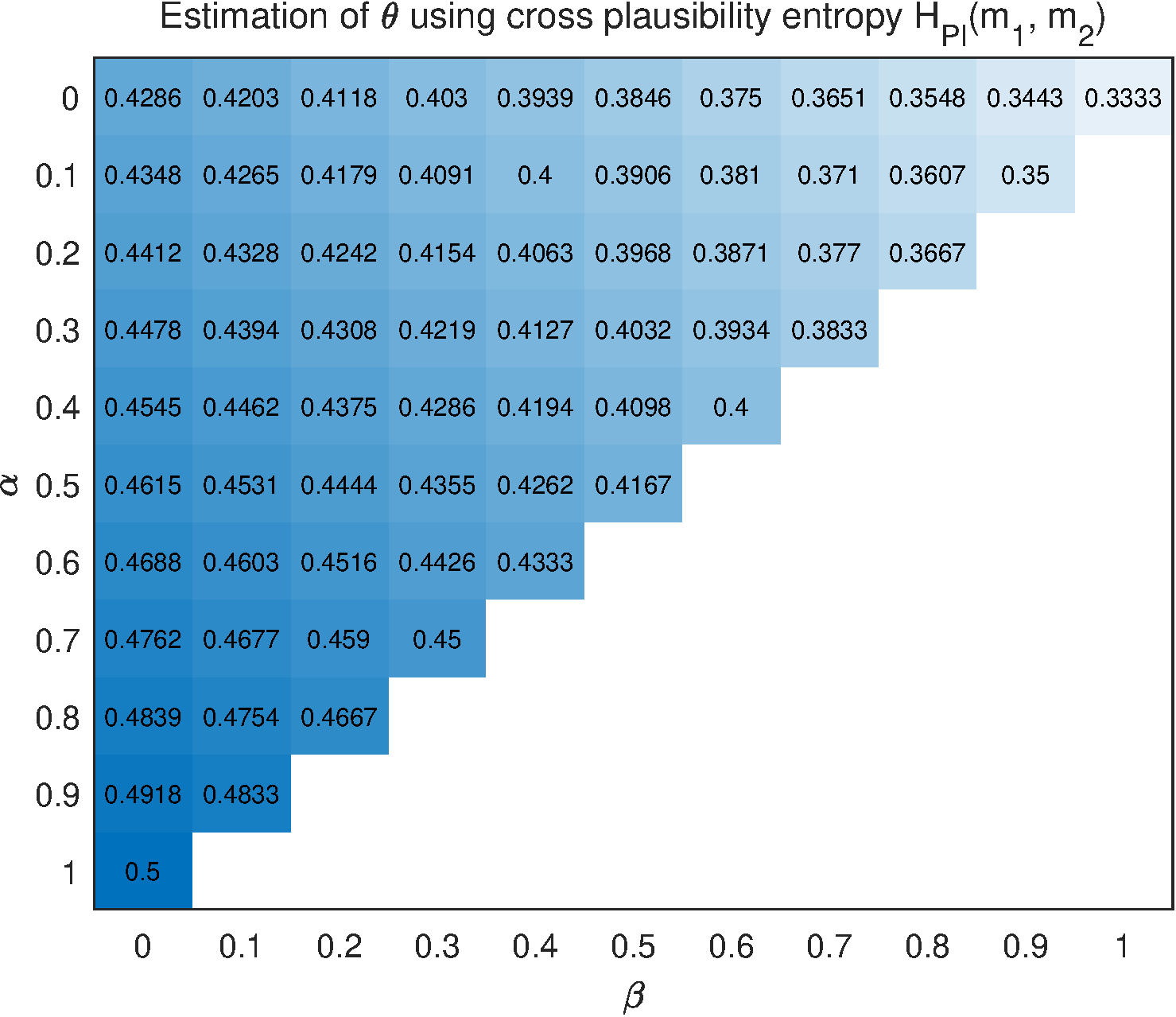
For the data set shown in Table 1, since there is uncertain observation $m_4$ involving epistemic uncertainty, the proposed cross plausibility entropy is used to calculate the total cross entropy loss $L_{Pl}$. Let $P$ be a distribution relying on parameter $\theta$ with $P\left(1\right)=\theta$ and $P\left(0\right)=1-\theta$, then

By letting $\frac{\partial L_{Pl}}{\partial \theta }=0$, we have

Figure 2 shows the results of using the proposed cross plausibility entropy with the consideration of different $\alpha$ and $\beta$. Compared with the results of $E^{2}M$ algorithm, the estimated $\theta$ is changing with $m_4$ having different uncertainty degrees. For example, for the cases of $m_4=m_4^1$ and $m_4=m_4^2$, it is obtained that ${\theta }_{Pl}^{1,\ast }=0.4333$ and ${\theta }_{Pl}^{2,\ast }=0.4462$.

Figure 2 Estimation of $\theta$ with the use of proposed cross plausibility entropy by considering different values of $\alpha$ and $\beta$.

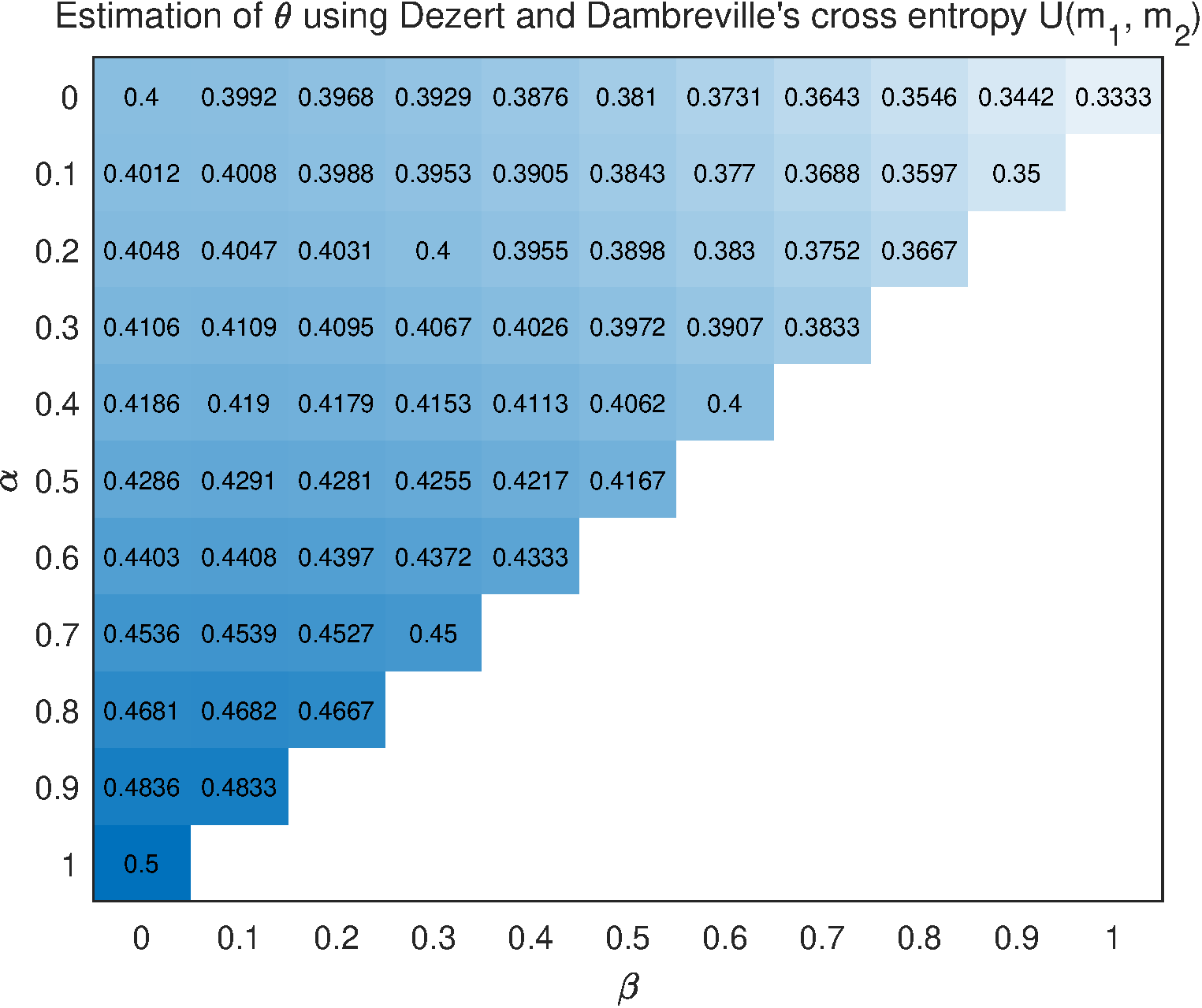
For the comparison, Dezert and Dambreville's cross entropy $U(m_1,m_2)$ is also used in the example to obtain the estimation of parameter $\theta$. Let $m_{\theta }$ be the estimation of $\theta$, in which $m_{\theta }\left(\left\{1\right\}\right)=\theta$, $m_{\theta }\left(\left\{0\right\}\right)=1-\theta -\epsilon$, and $m_{\theta }\left(\{1,0\}\right)=\epsilon$, where $\epsilon \to 0$. Then, in terms of Dezert and Dambreville's cross entropy, the total loss is

By means of $\frac{\partial L_U}{\partial \theta }=0$, it obtains

where $\epsilon \to 0$. Figure 3 graphically shows the results obtained by using Dezert and Dambreville's cross entropy $U(m_1,m_2)$.

Figure 3 Estimation of $\theta$ with the use of Dezert and Dambreville's cross entropy by considering different values of $\alpha$ and $\beta$.

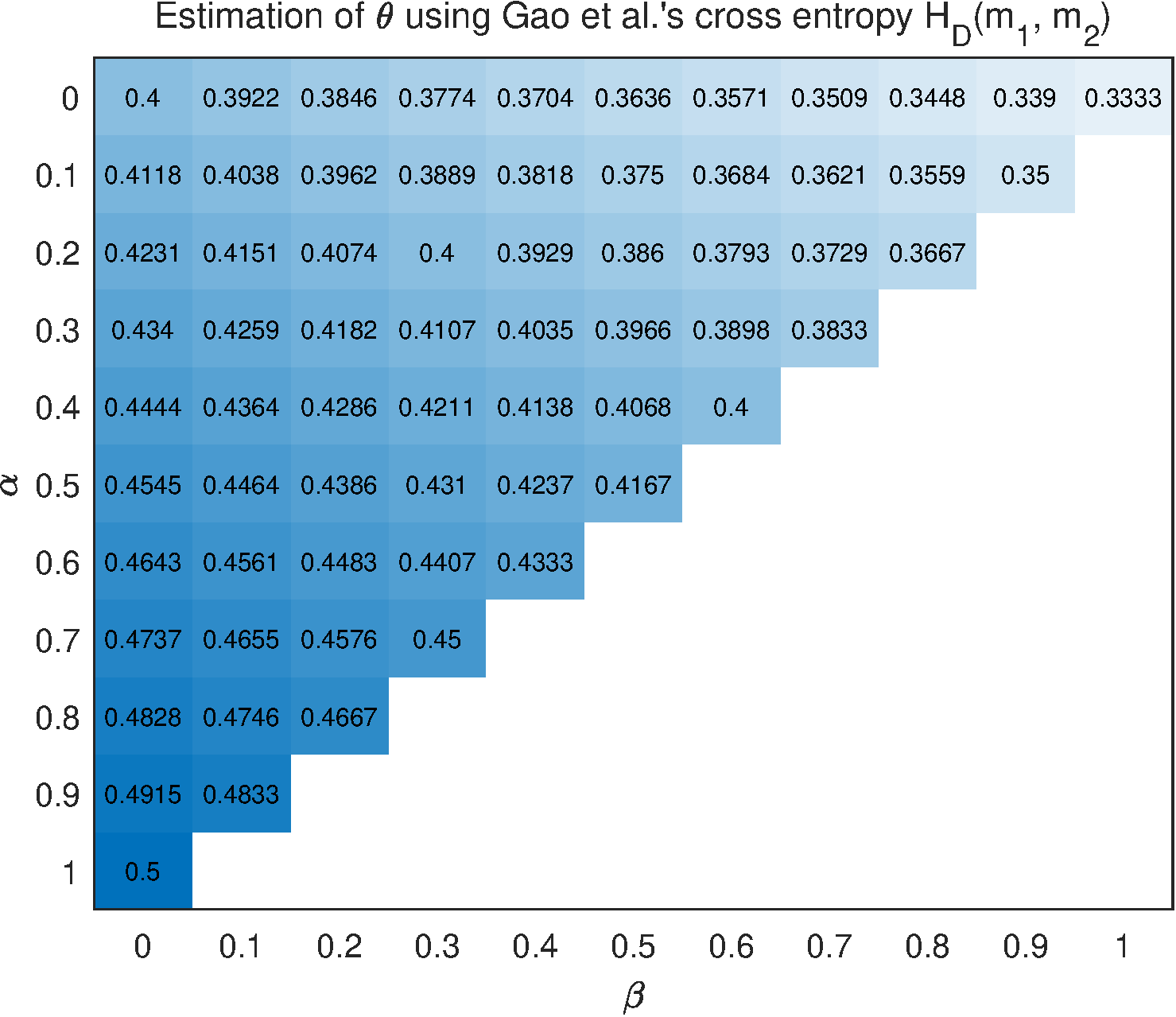
And the cross entropy $H_D(m_1,m_2)$ from Gao et al. [21] is also used in the example. Similarly, a total loss $L_D$ is calculated as follows

Then, the estimation of $\theta$ is derived via $\frac{\partial L_D}{\partial \theta }=0$ as below

in which $\epsilon \to 0$. The results with the use of cross entropy $H_D(m_1,m_2)$ are shown in Figure 4.

Figure 4 Estimation of $\theta$ with the use of cross entropy by considering different values of $\alpha$ and $\beta$.

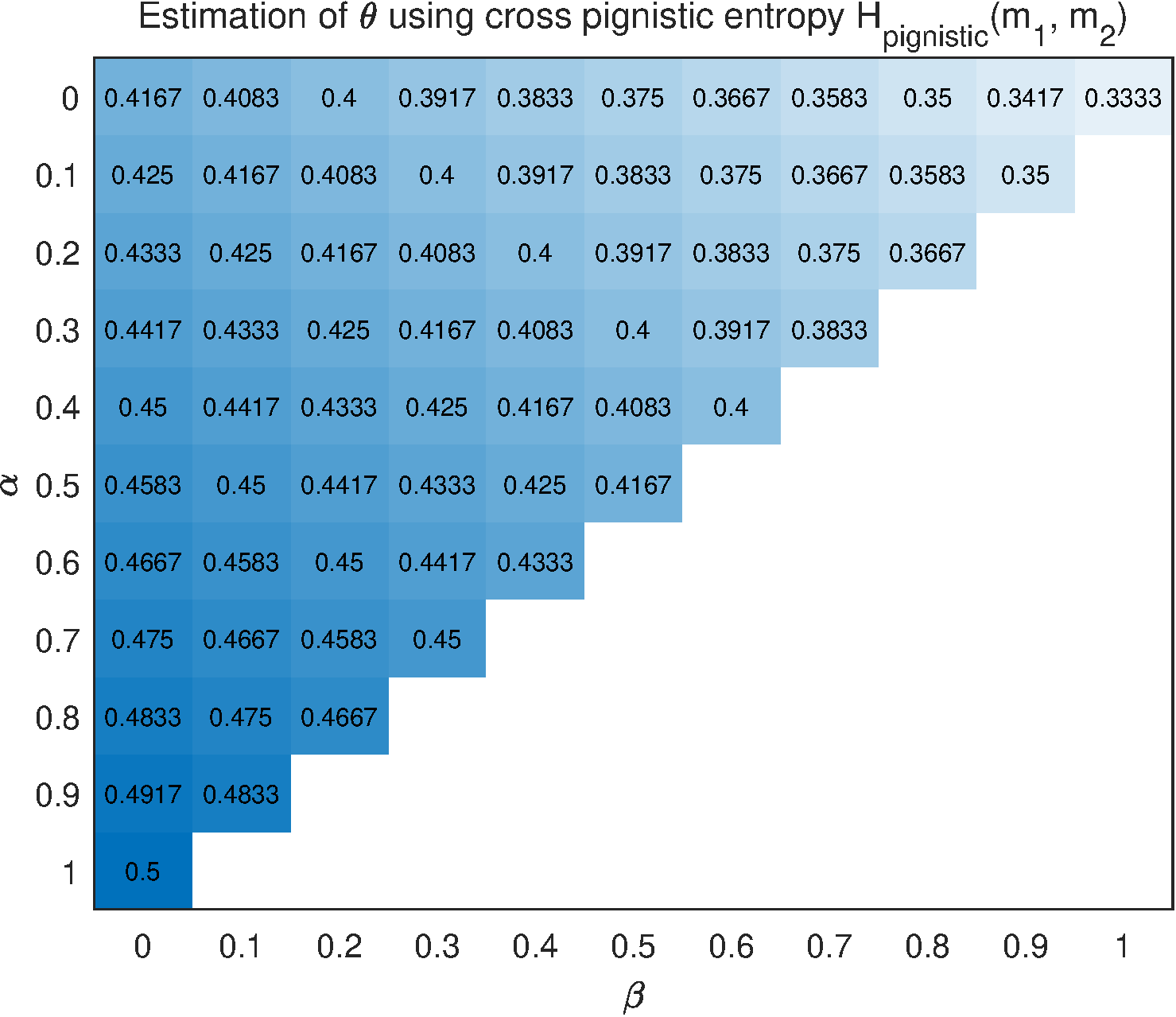
In addition, cross entropies inspired by two widely used entropies of mass functions, pignistic entropy [29, 4] and Yager entropy [30], are also considered for comparison. In terms of the formula of pignistic entropy $H_{\mathrm{pignistic}}\left(m\right)=-\sum _{{\theta }_i\in \Omega }{\mathrm{BetP}}_m\left({\theta }_i\right){\log }_2{\mathrm{BetP}}_m\left({\theta }_i\right)$, where ${\mathrm{BetP}}_m\left({\theta }_i\right)=\sum _{{\theta }_i\in A}\frac{m\left(A\right)}{\left|A\right|}$, cross pignistic entropy is naturally defined as $H_{\mathrm{pignistic}}(m_1,m_2)=-\sum _{{\theta }_i\in \Omega }{\mathrm{BetP}}_{m_1}\left({\theta }_i\right){\log }_2{\mathrm{BetP}}_{m_2}\left({\theta }_i\right)$. Then, a total cross entropy loss can be obtained by

where $P\left(1\right)=\theta$ and $P\left(0\right)=1-\theta$. By letting $\frac{\partial L_{\mathrm{pignistic}}}{\partial \theta }=0$, we have

whose graphical results with different values of $\alpha$ and $\beta$ are given in Figure 5.

Figure 5 Estimation of $\theta$ with the use of cross pignistic entropy by considering different values of $\alpha$ and $\beta$.

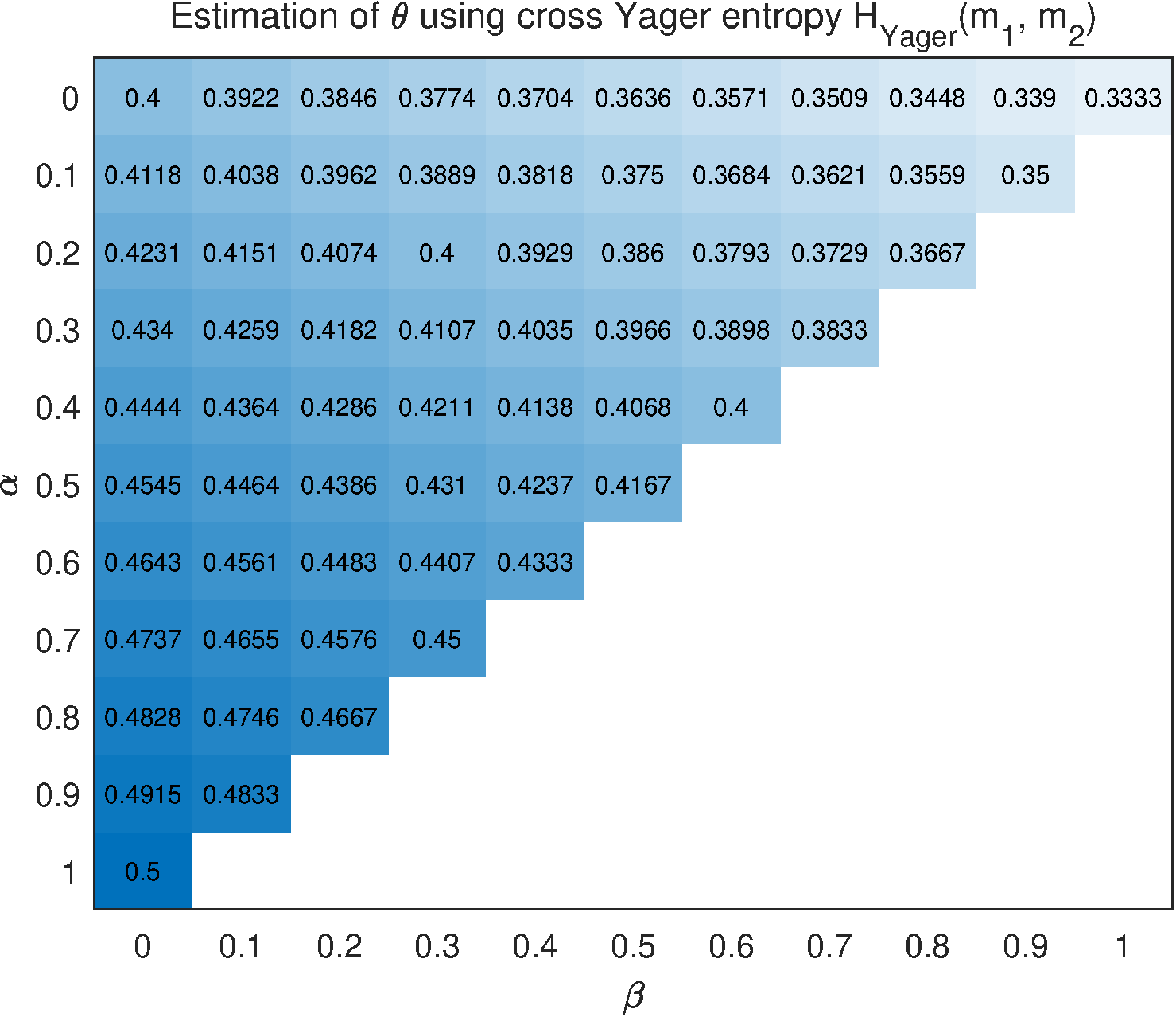
Similarly, according to the expression of Yager entropy $H_{\mathrm{Yager}}\left(m\right)=-\sum _{A\in \Omega }m\left(A\right){\log }_{2}P{l}_m\left(A\right)$, cross Yager entropy is defined as $H_{\mathrm{Yager}}(m_1,m_2)=-\sum _{A\in \Omega }{m}_1\left(A\right){\log }_{2}P{l}_{m_2}\left(A\right)$. Then, the corresponding total cross entropy loss is

By calculating $\frac{\partial L_{\mathrm{Yager}}}{\partial \theta }=0$, it obtains

which is same with ${\theta }_D^{\ast }$ that is obtained by using cross entropy $H_D(m_1,m_2)$. Figure 6 shows the results of using cross Yager entropy by considering different $\alpha$ and $\beta$.

Figure 6 Estimation of $\theta$ with the use of cross Yager entropy by considering different values of $\alpha$ and $\beta$.

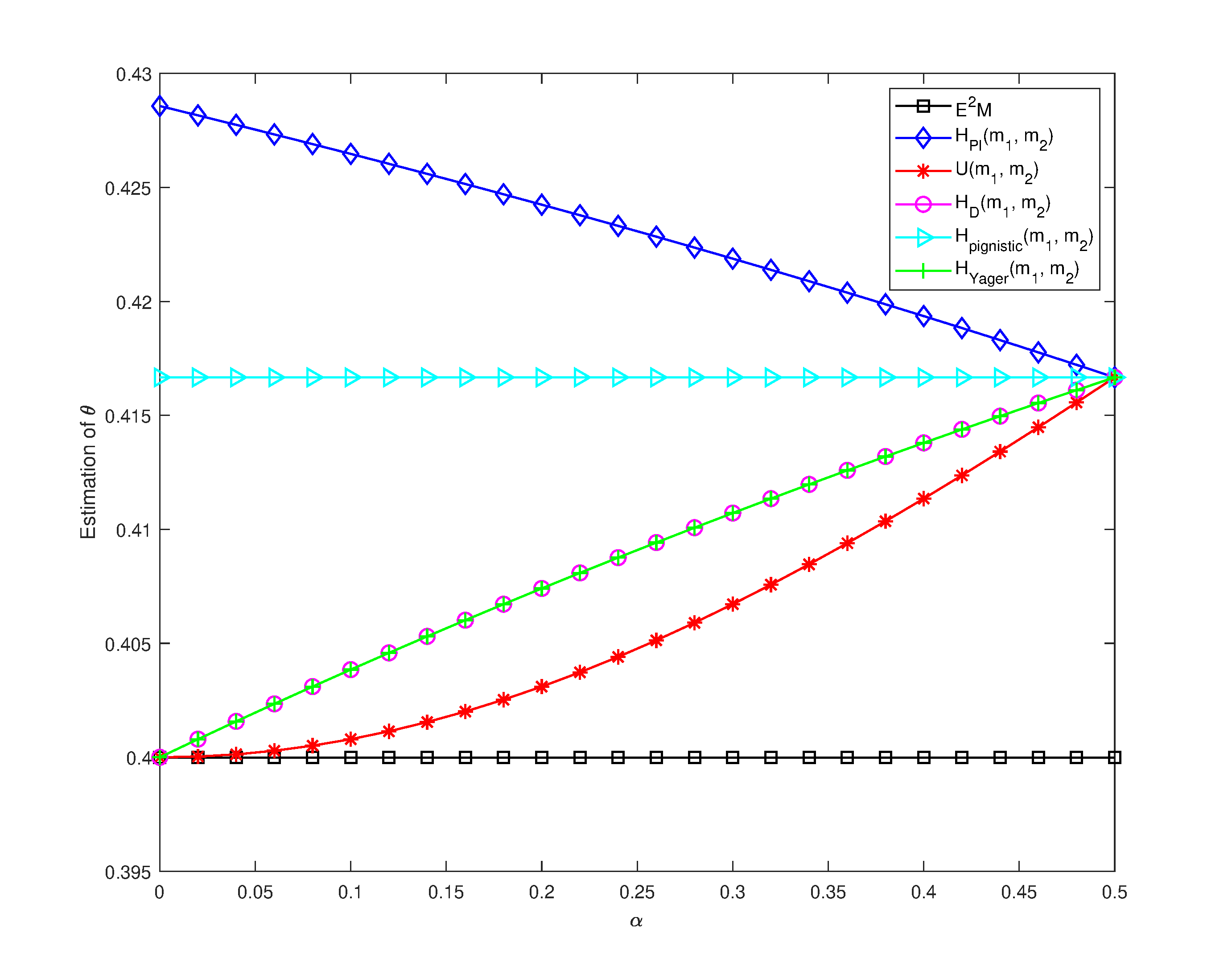
For the sake of further comparison of these methods, by letting $\alpha =\beta$, the uncertain observation $m_4$ becomes $m_4\left(\left\{1\right\}\right)=m_4\left(\left\{0\right\}\right)=\alpha$ and $m_4\left(\{1,0\}\right)=1-2\alpha$, where $\alpha \in [0,0.5]$. If $\alpha =0$, $m_4$ has the maximum uncertainty, and the uncertainty of $m_4$ is the least while $\alpha =0.5$. And it is noted that there is not any preference in $m_4$ between states $\left\{1\right\}$ and $\left\{0\right\}$ because $Be{l}_{m_4}\left(\left\{1\right\}\right)=Be{l}_{m_4}\left(\left\{0\right\}\right)=\alpha$ and $P{l}_{m_4}\left(\left\{1\right\}\right)=P{l}_{m_4}\left(\left\{0\right\}\right)=1-\alpha$. Figure 7 shows the estimation results of $\theta$ by using different methods for the case of new $m_4$ in which $\alpha =\beta$.

Figure 7 Estimation results of $\theta$ generated by using different methods where observation 4 is set as $m_4\left(\left\{1\right\}\right)=m_4\left(\left\{0\right\}\right)=\alpha$, $m_4\left(\{1,0\}\right)=1-2\alpha$.

In theory, if we only have observations 1,2,3,5,6, in terms of the maximum likelihood principle, the estimation of $\theta$ should be ${\theta }^{\ast }=2/5=0.4$. With the consideration of observation 4, i.e., unbiased $m_4$: (i)When $\alpha =0$, the estimation of $\theta$ should lie in the interval $[2/6,3/6]$ (whose midpoint is $2.5/6$) since the existence of epistemic uncertainty in observation 4 with $m_4\left(\{1,0\}\right)=1$; (ii) When $\alpha =0.5$, the estimation of $\theta$ should be $2.5/6$ since in this case the example becomes a mixture model for a two-dimensional Bernoulli distribution with $m_4\left(\left\{1\right\}\right)=m_4\left(\left\{0\right\}\right)=0.5$ in which there is only random uncertainty; (iii)In the process of increasing $\alpha$'s value from 0 to 0.5, the value of $\theta$ should be changing monotonically, because for the unbiased $m_4$ the only change is its uncertainty degree which is decreasing monotonically; (iv)Therefore, there is a path for the estimation of $\theta$ from start point ${\theta |}_{\alpha =0}\in [\frac{2}{6},\frac{3}{6}]$ to end point ${\theta |}_{\alpha =0.5}=\frac{2.5}{6}$.

From Figure 7, the result of $E^{2}M$ algorithm is not reasonable since the estimated $\theta$ is 0.4 when $\alpha =0.5$. Cross pignistic entropy $H_{\mathrm{pignistic}}(m_1,m_2)$ produces insensitive result for the change of observation $m_4$. The proposed cross plausibility entropy $H_{Pl}(m_1,m_2)$ gives that the value of $\theta$ is declining monotonically with the rise of $\alpha$, while Dezert and Dambreville's cross entropy $U(m_1,m_2)$, cross entropy $H_D(m_1,m_2)$, and cross Yager entropy $H_{\mathrm{Yager}}(m_1,m_2)$ present opposite trend of change. The difference between result of $H_{Pl}(m_1,m_2)$ and those of $U(m_1,m_2)$, $H_D(m_1,m_2)$, and $H_{\mathrm{Yager}}(m_1,m_2)$, is caused by the underlying logic of different entropy measures. The plausibility entropy is based on plausibility function and it tends to get the maximum uncertainty degree that a mass function could possibly have, therefore the cross plausibility entropy $H_{Pl}(m_1,m_2)$ gives a relatively big estimation of $\theta$. In contrast, it seems that $U(m_1,m_2)$, $H_D(m_1,m_2)$ and $H_{\mathrm{Yager}}(m_1,m_2)$ are to obtain relatively small estimation of $\theta$.

Compared with $U(m_1,m_2)$, $H_D(m_1,m_2)$ and $H_{\mathrm{Yager}}(m_1,m_2)$, the proposed $H_{Pl}(m_1,m_2)$ is more recommended in theory because, at first, the underlying entropy definitions of the formers are of some defects as analyzed in Section 4.1 and related references [19, 5], and the underlying mechanism of using cross plausibility entropy $H_{Pl}(m_1,m_2)$ to obtain the estimation of $\theta$ is more clear. In this example, with the use of cross plausibility entropy $H_{Pl}(m_1,m_2)$, the classical Bernoulli distribution based on probabilities is generalized to a new Bernoulli distribution with plausibility distribution observations as shown in Table 2. According to Table 2, the estimation of parameter $\theta$ can be obtained immediately as ${\theta }_{Pl}^{\ast }=\frac{3-\beta }{7-\alpha -\beta }$. Moreover, this Bernoulli distribution with plausibility distribution observations can be easily extended to the case of multi-dimensional Bernoulli distribution.

6. Conclusion

In this paper, new definitions of cross entropy and relative entropy of mass functions have been given on the basis of a recently presented total uncertainty measure of mass functions called plausibility entropy. And, properties of the cross plausibility entropy and relative plausibility entropy have been presented in the study. In addition, an illustrative example of application has been provided to show the effectiveness of the presented entropies compared with other methods and entropy definitions of mass functions. The presented cross plausibility entropy and relative plausibility entropy of mass functions can be used in the scenarios of multi-source information fusion based on Dempster-Shafer evidence theory for target recognition, fault diagnosis, and so on.

In the future study, on one hand, more theoretical analysis about the presented cross and relative plausibility entropies will be conducted; on the other hand, practical applications with the use of cross and relative plausibility entropies for multi-sensor information fusion, decision support systems, intelligent diagnosis, and so forth, will be further considered.