Chinese Journal of Information Fusion
ISSN: 2998-3371 (Online) | ISSN: 2998-3363 (Print)
Email: [email protected]


With the rapid development of big data technologies, deep learning has made remarkable strides in both theoretical research and practical applications of intelligent fault diagnosis [5, 3]. However, the success of these models hinges on the availability of large-scale, high-quality annotated data, which often entails substantial manual labeling costs [4]. This requirement severely limits the scalability and industrial deployment of deep learning-based diagnostic models, especially in scenarios with constrained annotation resources [1].
To address this bottleneck, cost-effective alternatives, such as crowdsourcing [6] and data-engine-driven automatic labeling [7], have been widely adopted. While these strategies significantly reduce annotation efforts, they inevitably introduce noisy labels—instances [8] where the annotated label deviates from the true class (). Such label noise distorts the data distribution, misaligns decision boundaries [9], and ultimately undermines both the accuracy and generalization of diagnostic models [10].
To enhance model robustness under noisy supervision, Learning with Noisy Labels (LNL) [11] has emerged as a prominent research direction. Two mainstream strategies have been extensively explored: sample separation [17] and label correction [12]. Sample separation aims to iteratively identify clean samples via model predictions and use only those for further training [13], while label correction refines noisy labels by integrating observed labels with predictive cues (e.g., latent features [14] or logits [15]). Despite their empirical success, both approaches suffer from a key limitation: they are heavily reliant on model predictions, which are themselves corrupted by noise [16], leading to the accumulation of confirmation bias during self-guided training.
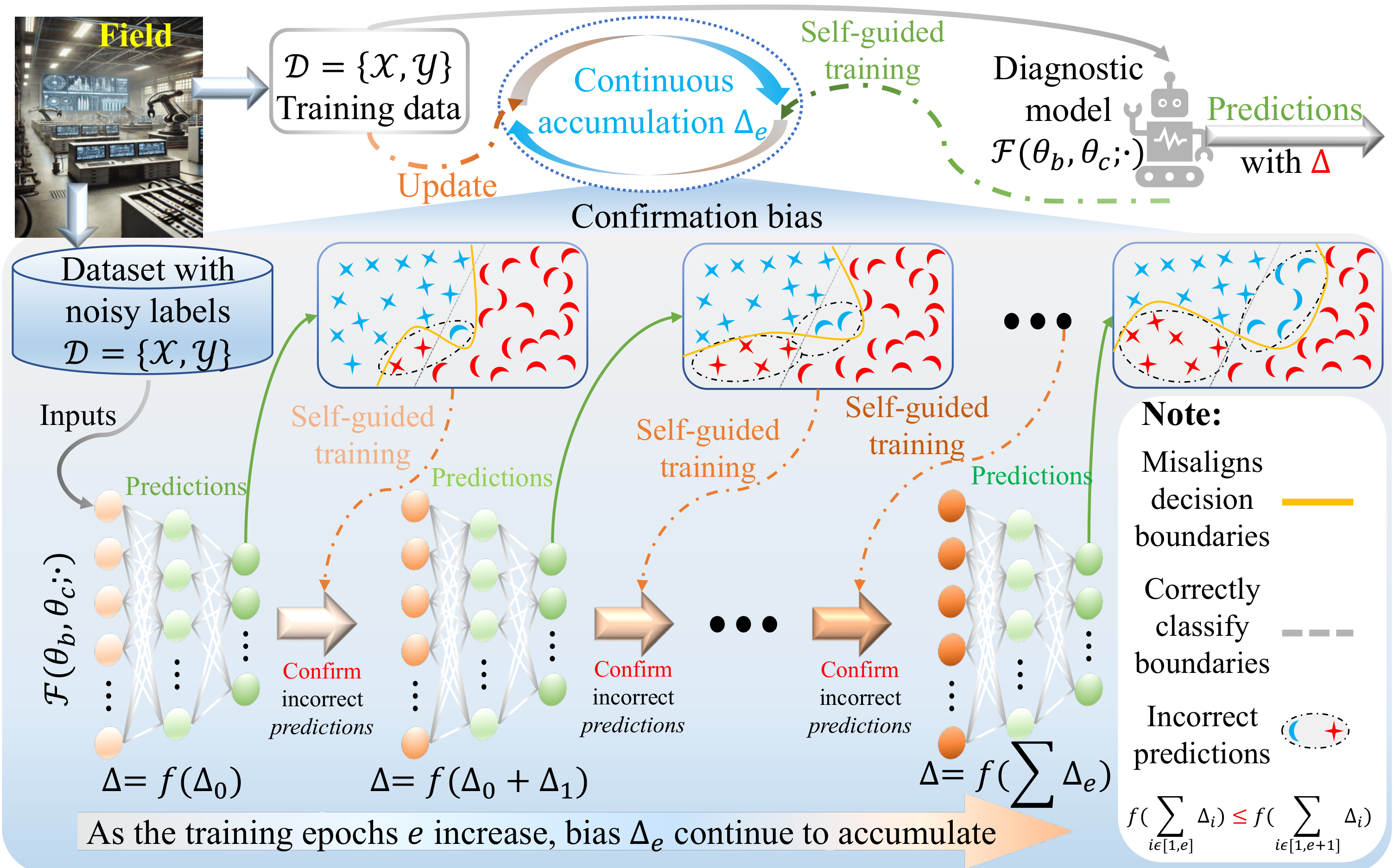
Essentially, these models are guided by their own decisions in noisy environments. Erroneous predictions may be repeatedly reinforced, eventually forming a biased representation of the data distribution (see Figure 1), which motivates the central question of this work:
How can we effectively leverage the full information of noisy datasets while mitigating confirmation bias caused by inaccurate predictions during self-guided training, in order to improve the generalization of diagnostic models under severe noise?
To address this challenge, we draw inspiration from quantum entanglement [18] and collapse, proposing a novel framework called "Multi-granularity Evidence Labels (MgEL)". MgEL constructs a set of multi-granularity labels by integrating three label sources: the original annotation labels , dynamically generated pseudo-labels , and probabilistic collapsed labels derived from the feature space. This process of combining two sub-distributional structures simulates the observation-collapse process of a quantum-entangled system, enabling more robust supervision in the presence of label noise.
Specifically, MgEL conceptualizes a feature cluster containing conflicting labels as a superposition state . The complex amplitudes are transformed into real-valued probabilities by borrowing the Born rule——to enable probabilistic reasoning. Beyond this, class-wise evidential values are introduced to quantify the "belief mass" that a sample belongs to each latent class (or basis state). These evidential values are not a direct conversion from the Born rule but rather are derived by modeling the internal distribution within each feature cluster under uncertainty, providing a structured representation of decision confidence.
Unlike conventional classification schemes that treat each sample as a single independent observation, MgEL constructs a pseudo-multi-source observation framework in the feature space, which better reflects the multi-view nature of real-world noisy data. The fusion of the original label , pseudo-label , collapsed label , and evidential simulates repeated observations across different measurement bases. This design suppresses overreliance on single predictions and alleviates the accumulation of confirmation bias, thereby improving robustness during training.
| Symbol | Description |
|---|---|
| Input sample with channels and time points | |
| Annotated label for | |
| Latent feature of extracted by the backbone network | |
| Randomly partitioned feature subspaces (entangled sets) | |
| Exponential cosine similarity between features and | |
| Feature cluster centered at | |
| Superposition state encoding class affiliation amplitudes | |
| Amplitude associated with class for sample | |
| Canonical basis vector for class | |
| Evidence vector obtained from pseudo-source fusion | |
| Multi-granularity fused label used for training | |
| Diagnostic model with backbone and classifier | |
| Estimated noise intensity for dynamic cluster adjustment | |
| Hilbert spaces of entangled subsystems and | |
| Model prediction vector for input | |
| Cross-entropy loss between prediction and label | |
| Training dataset containing noisy samples | |
| Pseudo-label derived via superposition collapse | |
| Collapsed label via multinomial sampling from | |
| Final fused label | |
| Clean class-conditional manifold for ground-truth label | |
| Feature extractor perturbed by label noise rate | |
| Noise-induced deviation of from its clean manifold | |
| Probability of class- label being flipped to class- |
We conduct extensive experiments on three fault diagnosis datasets to validate the effectiveness of MgEL, which demonstrate that MgEL outperforms other methods, particularly under scenarios with severe label noise (i.e., noise intensity ), significantly improving diagnostic accuracy and reducing sensitivity to annotation quality. These findings suggest that MgEL has the potential to reduce annotation costs and enable the reliable deployment of intelligent diagnostic models in practical industrial settings.
The key contributions of this work are summarized as follows:
Theory: We establish a pseudo-multi-source observation modeling method in the feature space, extending the theoretical foundation of decision-level information fusion.
Methodology: We propose a robust multi-granularity label construction strategy by introducing class-wise evidential values under uncertainty, which enhances the model's tolerance to noisy supervision.
Empirical validation: We conduct extensive experiments across three real-world fault diagnosis datasets with varying noise intensities. MgEL consistently outperforms baselines, especially under severe corruption (e.g., ), demonstrating its practical feasibility for robust learning under noisy supervision—though not yet deployed in full industrial pipelines.
To improve clarity and reduce potential ambiguity, Table 1 provides a formal summary of all key notations used throughout the paper.
Fault diagnosis with noisy labels is typically formulated as a multi-class classification task under annotation uncertainty [4]. Let the training dataset be , where each represents a multivariate time-series signal with channels and sampling points, and is the corresponding fault label drawn from predefined categories. These samples typically come from industrial systems, including mechanical, electrical, and structural components [21], where condition monitoring sensors collect time-series signals for predictive maintenance and fault detection [19].
In practice, noisy labels are prevalent due to multiple factors [20], including ambiguous or overlapping fault manifestations, inconsistencies among domain experts, and, more importantly, the limited reliability of automated annotation systems [23], which may mislabel large volumes of data due to heuristic rules or insufficient context [22]. Let denote the latent true label of . If , the sample is considered mislabeled. However, the noise distribution or transition matrix is typically unknown [24]. Depending on whether the noise occurs randomly or in a class-dependent fashion, it is commonly categorized as symmetric (uniform) or asymmetric (class-dependent)—the latter often reflecting realistic diagnostic confusion among fault types with similar signal patterns [13].
The learning objective is to construct a diagnostic model , comprising a backbone and a classifier , that maintains robust generalization to clean labels despite being trained on corrupted data, which can be formalized as:
Deep neural networks (DNNs) tend to overfit when trained on noisy labels, leading to poor generalization and unreliable predictions [26]. To address this, numerous strategies have been proposed to enhance model robustness under label noise [11], which are broadly categorized into three research areas: robust loss functions [27], sample separation [28], and label correction [29].
Robust loss functions reduce the negative impact of mislabeled samples during training. For example, SCE [30] includes a symmetric regularization term to reduce the dominance of noisy labels, while NLS [31] uses label smoothing to lower label confidence. However, these approaches often rely on strong assumptions about the noise distribution, such as the need for access to or accurate estimation of the label transition matrix , which is difficult to obtain in practical scenarios [32].
A second class of methods focuses on sample separation, aiming to distinguish clean from noisy samples based on training dynamics. Many early works exploit loss-based heuristics, assuming that samples with lower loss are more likely to be correctly labeled. Representative methods include JoCoR [33], which trains peer networks on mutually selected small-loss samples to refine the dataset. More recent approaches, such as DISC [25], introduce memory-based dynamic thresholding to categorize training data into clean, hard, and correctable subsets. However, these methods depend fundamentally on the model's own predictions to estimate sample reliability. As a result, incorrect assessments during early training stages may be reinforced across epochs—this phenomenon is known as confirmation bias (see Figure 1). Even dynamic sample selection strategies cannot fully overcome this limitation, as the thresholds are still updated based on past model behavior [34].
To mitigate data underutilization caused by sample removal, label correction approaches that generate pseudo-labels from model predictions to supervise training have emerged as a promising alternative [35]. For instance, SED [32] uses a mean-teacher framework to stabilize label updates. Despite their effectiveness, these methods also suffer from confirmation bias: initial incorrect predictions can propagate and become increasingly difficult to reverse during subsequent training [16].
This shared limitation in both sample separation and label correction methods arises from their "self-guided" nature—they rely solely on the model's internal signals, making them vulnerable to early-stage errors that propagate unchecked. To overcome this, inspired by principles of quantum mechanics, MgEL emulates the repeated observation-collapse mechanism of entangled quantum systems, introducing controlled uncertainty throughout the training process. By periodically re-evaluating fused labels with multi-granularity representations, MgEL disrupts confirmation bias and prevents training from being overly influenced by prior incorrect predictions. In this way, MgEL fully leverages the information contained in the original dataset, even when labels are partially corrupted, and improves the robustness of the corrected supervision signals.
This work extends our earlier research on learning with noisy labels, specifically MgCF [40] and MgL [41], both of which leverage feature clustering for robust label correction. Although MgCF, MgL, and the proposed MgEL share a unified design philosophy: transforming noisy labels into structured supervision via latent-space modeling, they differ significantly in terms of label granularity representation, fusion strategy, belief assignment, and computational scalability. To clarify these distinctions and avoid any confusion regarding academic overlap, we provide a comparative analysis, also visually summarized in Figure 2.
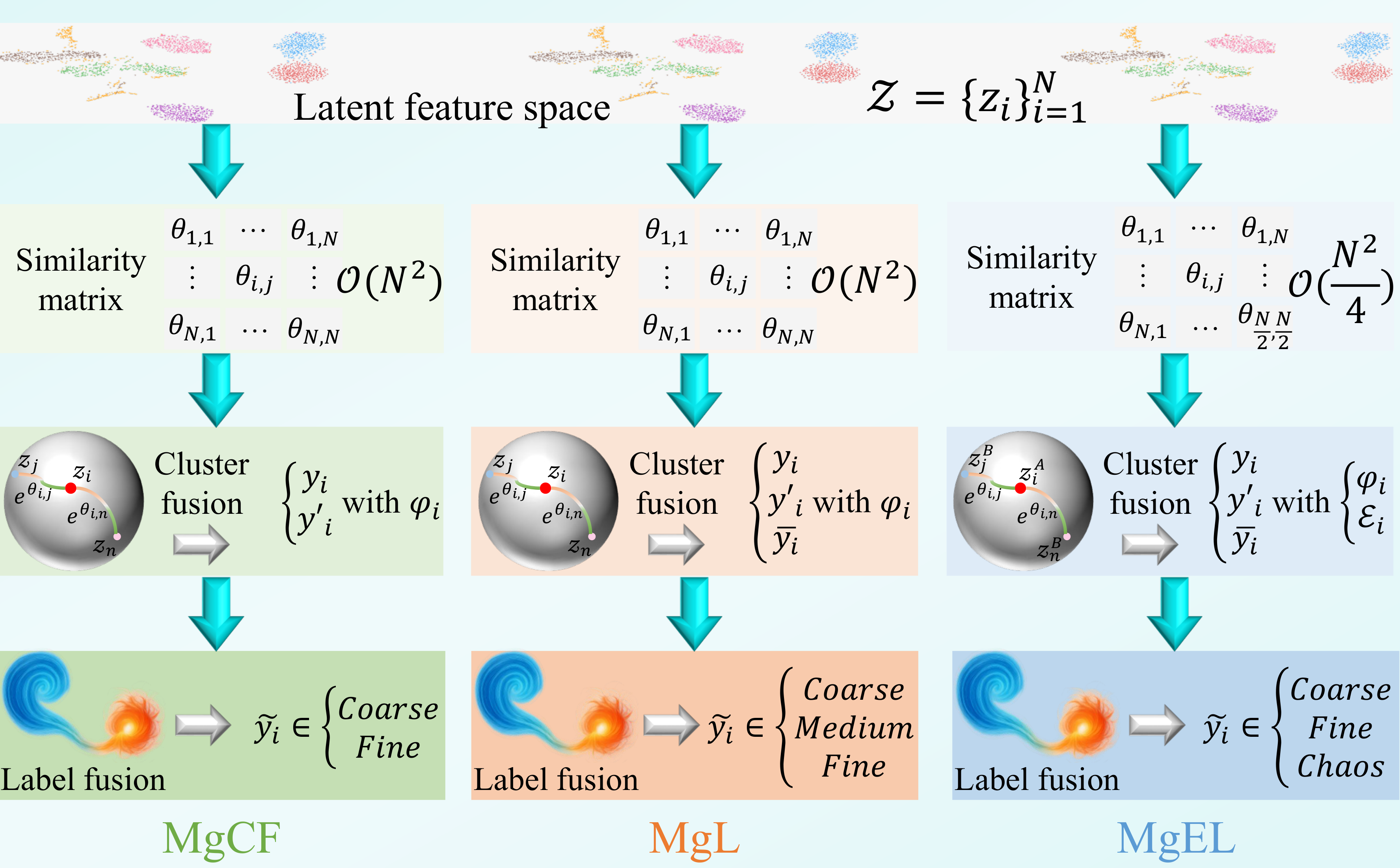
First, regarding label granularity semantics, all three frameworks aim to suppress confirmation bias by constructing multi-granularity supervisory signals. In this context, MgCF introduces a dual-granularity labeling scheme: fine-grained labels are formed when annotation and pseudo-labels agree, indicating high class certainty, whereas coarse-grained labels are used when disagreement occurs, signaling ambiguity. MgL builds on this structure by incorporating an additional label source—the collapsed label sampled from the superposition state —which allows the construction of medium-grained labels when only partial agreement exists among the three sources (annotation, pseudo, collapsed). In contrast, MgEL reverts to a two-level granularity structure as in MgCF but complements it with a downstream decision deferral mechanism that handles fully inconsistent labels by reverting to the original superposition state . While this does not introduce an explicit third granularity level, it implicitly absorbs semantically hesitant cases through adaptive rejection, thereby preserving the interpretive flexibility offered by multi-granularity labeling.
In terms of label fusion mechanisms, both MgCF and MgL directly use the fused multi-granularity label as the supervisory signal in training. MgL distinguishes itself by explicitly incorporating collapsed labels into the fusion rule alongside annotations and pseudo-labels, thus enabling medium-grained representations. MgEL, in contrast, restricts the fusion to annotation and pseudo-labels but introduces a Coherence Mechanism (Sec. 3.5) that evaluates whether any two of the three available labels (annotation, pseudo, collapsed) are consistent. If no consistency is found, the fused label is rejected and replaced with , effectively reverting supervision to a probabilistic representation. This mechanism guards against overconfident but unreliable updates and introduces an adaptive rejection pathway not present in either MgCF or MgL.
The belief assignment strategies adopted by the three methods also exhibit fundamental differences. In both MgCF and MgL, the amplitude probabilities derived from the superposition state —which reflects the relative class distribution within each feature cluster—are directly treated as empirical belief masses. These unregularized values are used to assign fusion weights between annotations and pseudo-labels, implicitly treating intra-cluster frequencies as reliable class evidence. In contrast, MgEL introduces a belief regularization mechanism. Rather than using the raw amplitudes in , MgEL calibrates the belief assignment by incorporating a global noise estimate , constructing an evidential vector that reflects class-wise reliability under dataset-level uncertainty. This transformation from empirical frequencies to noise-aware belief masses enhances the robustness of label fusion, particularly in high-noise scenarios, and aligns with the principles of uncertainty modeling in evidential reasoning frameworks.
Finally, in terms of computational scalability, MgCF and MgL both compute global similarity matrices of size to construct feature clusters across the full dataset, which incurs substantial memory and runtime costs. MgEL, inspired by the partitioned structure of entangled quantum systems, proposes an entangled subspace design: the latent feature space is randomly split into two disjoint subsets, with each sample querying only across the opposite subspace. This reduces similarity computation to and introduces randomization effects similar to dropout. This modification not only improves training efficiency but also enhances cluster robustness by avoiding deterministic, potentially biased global modeling.
In summary, MgEL consolidates and extends the prior frameworks by integrating evidential trust modeling, a coherence-driven rejection mechanism, and a more scalable partitioned clustering strategy. These contributions allow it to generalize effectively across high-noise environments while maintaining theoretical and algorithmic distinctions from both MgCF and MgL.
In quantum mechanics, the observation-collapse mechanism explains how the measurement of one particle in an entangled system causes the entire wavefunction to collapse instantaneously into a corresponding eigenstate [36]. This collapse not only determines the measured particle's state but also instantaneously defines the state of its entangled counterpart, reflecting a non-local correlation [37]. This principle embodies measurement-induced state transitions and decision outcomes under uncertainty [38], providing rich inspiration for information fusion in noisy, uncertain environments.
Formally, we consider a bipartite quantum system composed of two subsystems and , with a joint entangled state expressed as:
where denotes the overall quantum state in the composite Hilbert space , with and denoting the Hilbert spaces of subsystems and , respectively. The vectors and are orthonormal eigenstates of the respective subsystems, and is the complex amplitude associated with each joint basis pair, normalized such that . The index enumerates the possible entangled basis components, forming the mathematical foundation of our analogy.
Upon measuring subsystem and obtaining the outcome , the entire system collapses into the product state , with a probability of . This structure implies that the state of is instantaneously determined by observing , without direct interaction with . Such non-local inference allows one subsystem to act as an informational proxy for the other—a foundational feature of quantum entanglement.
In MgEL, this collapse mechanism serves as a conceptual inspiration, rather than a physical simulation. We draw an analogy between the measurement-induced resolution of uncertainty and the process of integrating multiple label sources into a consistent supervisory signal. Concretely, three label sources are constructed for each sample: (I) the original annotation, (II) a pseudo-label corresponding to the maximum-amplitude component in the superposition state, and (III) a collapsed label probabilistically sampled based on the amplitude distribution. These label sources represent diverse, imperfect observations of the same latent feature representation.
To further emulate the informational interdependence observed in entangled systems, we partition the latent feature space into two disjoint subspaces, and , and construct feature clusters through cross-subspace querying—samples in are clustered based on their similarity to samples in , and vice versa. This design allows feature clusters derived from one subspace to act as interpretive surrogates for evaluating the class membership of samples in the other. In doing so, each subspace imposes a structural constraint on its counterpart, akin to the inference structure in bipartite entanglement. Additionally, since each sample observes only a subset of the latent space per epoch, this formulation introduces Dropout-like stochasticity, reducing memory complexity and enhancing generalization.
When partial agreement arises among the constructed label sources, it is interpreted as a consistency-triggered decision signal, and the fused label is then adopted for training. Conversely, when all sources disagree, no definitive decision is made; the model retains the superposition-based representation, deferring commitment due to measurement incoherence.We emphasize that all quantum-theoretic terminology is used metaphorically to guide the modeling of uncertainty, structural supervision, and decision consistency. No physical entanglement or non-local interaction is simulated or implied.
To theoretically examine whether extreme label noise (e.g., ) induces structural shifts in the latent space, we first formalize the notion of label-induced manifold perturbation. We posit that such shifts do not alter the marginal distribution but instead distort the conditional representation learned by the model. The following assumption summarizes our conclusion:
We now justify Assumption 1 through formal modeling and analysis.
Let denote a clean training sample, and the observed (potentially corrupted) label. Due to the incorrect supervision, the model learns a perturbed representation:
where denotes the feature-level perturbation induced by the label error. Since this perturbation accumulates over multiple training steps via gradient descent, we express it as:
We consider the label corruption process governed by a class transition matrix with . The induced perturbation distribution is thus:
where denotes the no-perturbation case (correct labels), and is a distribution over perturbations generated by incorrect labels sampled according to .
This mixture formulation in Eq. 5 provides a unified framework for modeling both symmetric and asymmetric label noise. In the symmetric case, where for all , the perturbation distribution approximates an isotropic Gaussian, i.e., . In contrast, under asymmetric noise where is sparse and class-dependent, becomes a mixture of Gaussians with non-zero means, as defined in Eq. 6.
We define the manifold perturbation error (MPE) as follows:
and hence,
where is the effective covariance structure aggregated over the perturbation distribution. This result confirms that as increases, the average deviation from the class-specific latent manifold grows linearly, reflecting a progressive distortion in .
To quantify the global structural deformation, we define the manifold distortion index (MDI) as:
The derivation above substantiates the hypothesis in Assumption 1 by showing how high-intensity label noise induces representation-level perturbations that scale with both the noise rate and the structural properties of the label transition matrix . In particular, the manifold distortion index provides a global quantitative measure of such perturbations, confirming that noisy supervision leads to a pseudo distribution shift that manifests not in the input space but in the conditional representation space . This shift disrupts the geometric coherence of latent class manifolds and ultimately impairs generalization performance.
These findings motivate the core design of MgEL: to suppress the emergence and propagation of noise-induced structural drift by fundamentally rethinking how label supervision is incorporated during training. Rather than relying solely on potentially corrupted labels or unstable model predictions, MgEL introduces controlled structural uncertainty and diversified supervisory signals to counteract the convergence toward biased representations. This is achieved not by architectural overhauls or post hoc corrections, but by embedding uncertainty-aware regularization into the label construction process itself. By doing so, MgEL aims to retain the semantic integrity of the class manifolds even under extreme noise, thereby preserving the model's capacity for generalization.
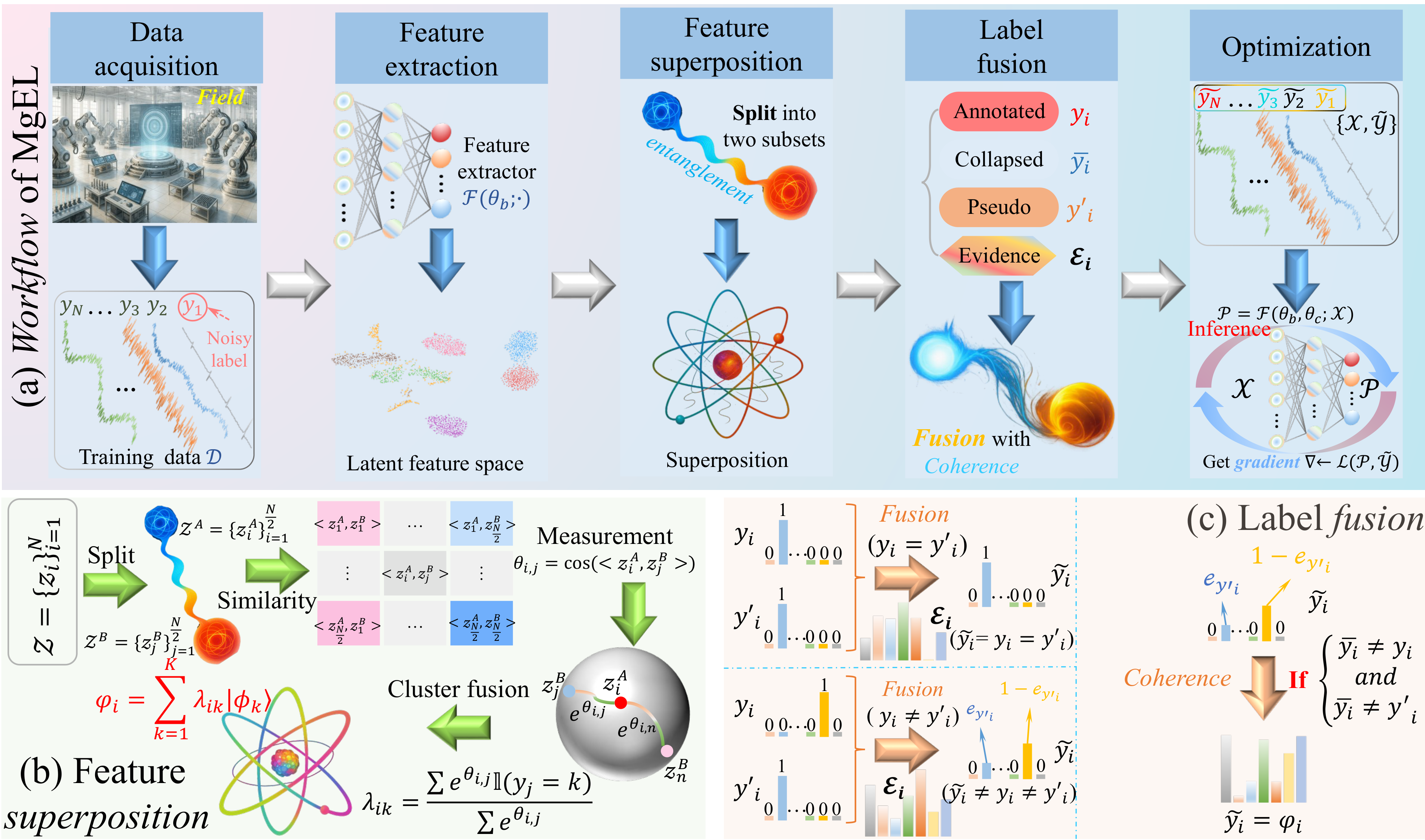
DNNs with strong generalization capabilities tend to induce class-discriminative clustering structures in the latent feature space [16], where the similarity between two sample embeddings reflects the likelihood that they share the same true class. Empirical observations confirm [40] that the closer two representations are, the more likely .
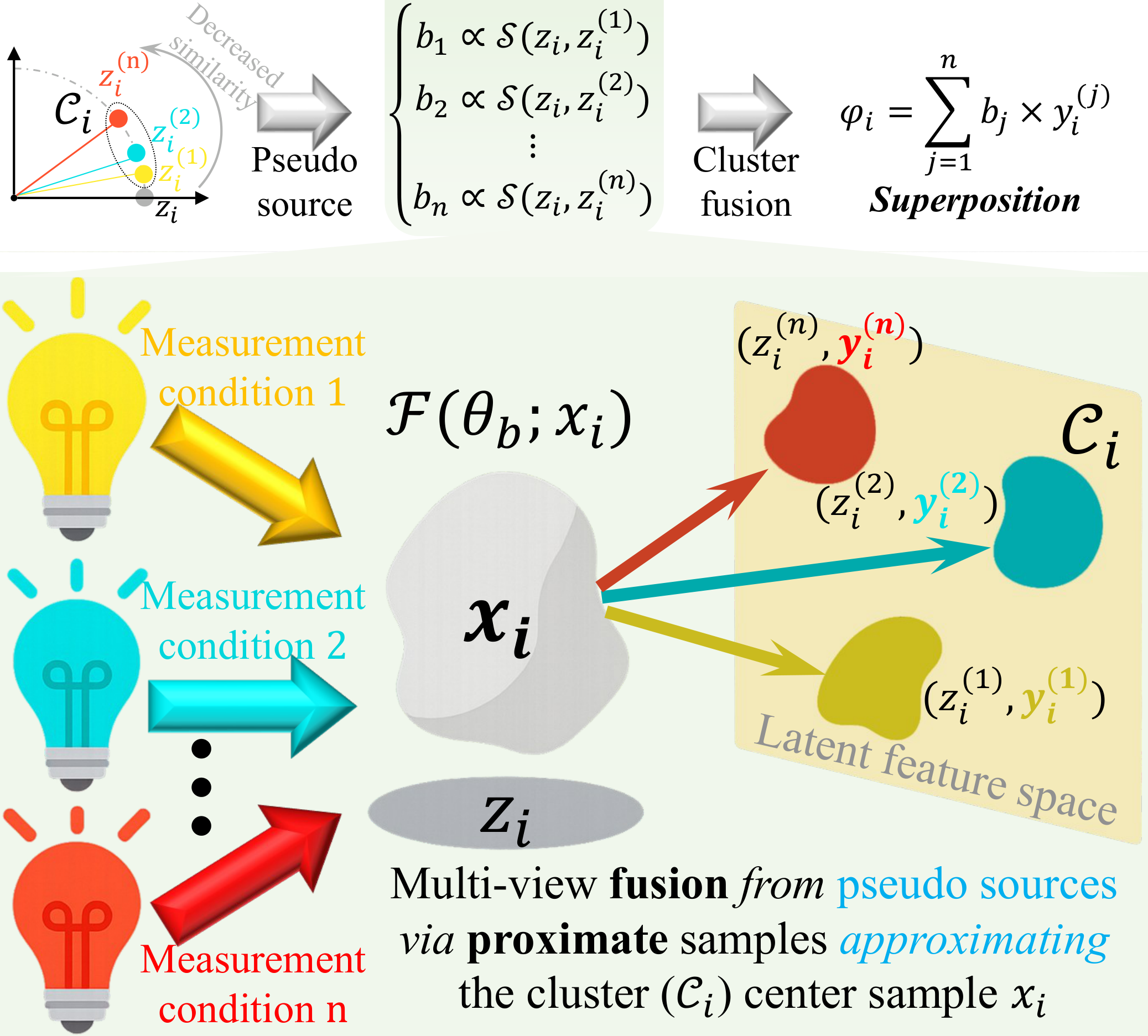
Motivated by Assumption 2, MgEL (see Figure 3) draws inspiration from the observation-collapse process in quantum entangled systems. To simulate such a system, the latent feature space is randomly divided into two disjoint subsets, and . For a sample , a feature cluster is formed by retrieving its top- most similar neighbors, each associated with the observed annotation . These cluster members are treated as independent observations of under different measurement conditions, with their label distribution abstracted as a probabilistic superposition over possible class outcomes.
Through these local observations, MgEL simulates multi-view fusion from pseudo sources by leveraging the structured observations of these clusters (see Figure 4). Specifically, for each sample , a pseudo-label is derived from the distribution of labels in its feature cluster. This pseudo-label is then fused with the original annotation to create an evidence-aware multi-granularity label . Based on the principles of Dempster-Shafer theory (DST) [39], we interpret the label distribution in the feature cluster as a class-supporting evidence mass function. The fusion process assigns different weights to the pseudo and observed labels, reflecting their respective levels of credibility under uncertainty.
To further enhance interpretability and control, MgEL categorizes the fused label into two levels of semantic granularity based on the consistency between the pseudo-label and the annotation . When the two labels are identical, the fused result is interpreted as a fine-grained confident label, reflecting strong agreement across sources and indicating high certainty in the class assignment. In contrast, if the pseudo and original labels disagree, the resulting label is considered a coarse-grained hesitant label, capturing ambiguity in the sample's class attribution and preserving the possibility of it belonging to multiple candidate classes.
Since this correction is based on model-generated latent representations and predictions, it risks amplifying confirmation bias during self-guided training. To mitigate this, MgEL introduces a coherence mechanism that assesses the consistency among multiple label sources (pseudo, original, collapsed). When inconsistency is high, the fused label is reverted to its superposition state , preserving uncertainty and deferring final decisions until further optimization.
Overall, MgEL reinterprets noisy or conflicting labels as structured evidence, offering a principled framework to improve robustness by aligning quantum-inspired modeling with uncertainty-aware label correction.
Consider a noisy dataset with latent representations extracted using a backbone network .
Drawing upon quantum collapse dynamics and superposition principles, we establish a pseudo multi-source label fusion framework where each latent representation models an analogous quantum state. Central to this approach is the entanglement-emulating partition: undergoes random bisection into disjoint subsets and of equal cardinality. This bipartite configuration achieves two objectives: reducing computational complexity of similarity tensors from to and implementing stochastic structural dropout.
Furthermore, each subset acts as an independent measurement apparatus, simulating the observational asymmetry inherent in quantum systems. The bipartite design is a deliberate computational compromise. While multi-partite partitioning () incurs prohibitive complexity and generates intractable similarity tensors, the current formulation maintains theoretical fidelity while ensuring computational tractability.
For each sample , neighborhood retrieval is performed exclusively from the complementary subset. These neighbors are not merely correlated instances but simulate independent measurements of the underlying quantum state. Each neighbor thus represents an eigen-label state (class collapse) under different measurement contexts. This quantum interpretation underpins the formulation of the superposed label state:
where encodes amplitude-based label uncertainty, with coefficients quantifying class evidence strength (see Sec. 3.3). Neighborhood retrieval uses exponentially transformed cosine similarity to circumvent the curse of dimensionality.
Based on Assumption 2, for , with latent representation , we identify its most similar feature vectors from the entangled subset to form a feature cluster . These neighbors are ranked such that
To quantify sample similarity, we use an exponential cosine similarity function (see Eq. 8). This decision is motivated by the well-known phenomenon of distance concentration in high-dimensional spaces, which makes traditional distance metrics, such as Euclidean distance, ineffective. Specifically, for two normalized vectors , the squared Euclidean distance is defined as:
Assuming , we have:
where is the angle between and . As dimensionality , most angles , and hence , implying:
which leads to the so-called concentration of measure, where almost all pairwise distances converge to a constant. Formally,
making it nearly impossible to discriminate between samples based on Euclidean distance.
To avoid this, we use the cosine similarity:
which measures angular similarity and is less sensitive to magnitude and dimensionality. Still, in high dimensions, even cosine similarities between neighbors may vary only slightly. To accentuate such differences, we introduce the exponential transformation:
This maps cosine similarity from to , i.e. , nonlinearly amplifying differences between close neighbors and enabling sharper separation of structurally similar samples in latent space.
Based on this similarity, the feature cluster is formally defined as:
The cluster size is dynamically adapted based on the estimated noise intensity (see Sec. 3.4) from the previous training epoch:
In this work, and . This allows the framework to flexibly adjust the neighborhood scope: under high noise, more neighbors are included to stabilize superposition formation; under low noise, smaller clusters avoid introducing irrelevant variance.
Cluster fusion simulates the integration of multiple pseudo-observations by leveraging the feature and label distributions within the feature cluster (as constructed in Eq. 9). This process is analogous to quantum state tomography [42] in quantum mechanics, where the quantum state is reconstructed by sampling probability distributions across different measurement bases, determining the amplitude probabilities of the eigenstates in a superposition.
In MgEL, the superposition state constructed for each sample can be interpreted as the probability distribution of 's class membership across all potential categories. The associated belief mass encodes the basic belief assignment for each class, which is used to fuse the pseudo-label and the original annotation during label correction, considering the current dataset's noise level.
To improve the robustness and accuracy of the superposition state , MgEL adopts the evidence combination concept from DST. Each sample in the feature cluster is treated as an independent source of evidence, and a cluster-based fusion process based on similarity is designed:
where represents the total number of classes, and is an indicator function that equals 1 when , and 0 otherwise.
Using this similarity-based fusion method, MgEL combines the feature distribution and label frequency information within the feature cluster to form the superposition state . This enables MgEL to robustly model the class membership probability distribution for sample , even in noisy and uncertain environments.
However, considering the potential misleading effects of noisy labels, there is a risk that the feature mapping during training may inaccurately represent the data, leading to imprecise class probabilities in . If these probabilities were directly used as fusion belief masses for label correction, they could amplify errors and introduce confirmation bias.
To address this, MgEL does not use 's class probabilities directly as belief masses in the fusion of annotations and pseudo-labels. Instead, after considering the estimated noise intensity , MgEL adjusts the evidence for each class membership distribution:
After obtaining the superposition state and class evidence through feature cluster fusion, MgEL generates pseudo-labels using the maximum posterior decision rule (commonly applied in multi-class classification tasks, e.g. [1]). The amplitude probability associated with the pseudo-label represents the frequency or intra-cluster label consistency of the dominant class within the feature cluster. This is used to estimate the noise intensity of the current dataset by calculating the mean label consistency across all feature clusters:
At this stage, both the pseudo-label and the original annotation label serve as independent evidence sources for making decisions about sample . MgEL then fuses these two sources to correct the noisy labels, based on their respective confidence levels. Specifically, if the pseudo-label and original annotation labels agree, it is highly likely that the original annotation is not noisy and can be used for training. In contrast, when the two labels disagree, the pseudo-label is more likely to be accurate. The confidence in the decision-making process is captured by the evidence vector , which is derived from the pseudo-source fusion.
This allows the original annotation label to be corrected toward the pseudo-label, with a weighted confidence:
The fused multi-granularity labels integrate both fine-grained and coarse-grained information, reflecting the model's certainty in the predicted class. When the pseudo-label and the original annotation agree, the label corresponds to a fine-grained confident label, offering a more precise supervision signal. When the labels disagree, the output represents a coarse-grained hesitant label, with the decision uncertain between two potential classes, and the confidence distributed between them according to the evidence mass . This distinction allows the model to dynamically adjust its decision-making process based on the consistency of the label sources.
To mitigate the confirmation bias that may arise from directly using pseudo-labels to correct original annotations, MgEL employs a resampling strategy on the superposition state , simulating a random collapse process. This generates a collapsed label , where the sampling probability for each class corresponds to the amplitude probability of the corresponding eigenstate in .
Subsequently, MgEL introduces a Coherence mechanism triggered by label consistency. Before performing supervised training, the fused labels go through an additional processing step. In this step, the system accepts a fused label only when at least two of the following labels are consistent: the original annotation , the pseudo-label , and the collapsed label . If none of these labels are consistent, the system retains the superposition state , deferring the final label commitment until more evidence is provided in subsequent training iterations.
The update rule for the fused label is formally defined as follows:
In this rule, represents the norm of the vector formed by the sum of the three labels, and the condition ensures that the fused label is accepted when at least two of the three labels are consistent.
Through this process, MgEL combines the statistical consistency of the pseudo-labels, the randomness introduced by the collapsed labels, and the original annotation labels to create more robust labels . This approach reduces the confirmation bias typically associated with prediction-based label correction and improves the model's generalization ability, especially in high-noise environments.
The Alg. 1 summarizes the key steps of MgEL, integrating feature clustering, pseudo-label generation, and evidence-based label fusion for label correction, simulating quantum-inspired mechanisms and adapting them for noisy label correction.
Noisy dataset , model , estimated noise intensity
# Trained diagnostic model
Initialize model ,
for epoch in range(Total Epochs) do
# Extract latent features
# Partition dataset into two subsets
, # Construct feature clusters via Eq. 9
, # Compute superposition state via Eq. 11
# Get class evidence via Eq. 12
# Estimated noise intensity and compute pseudo-labels via Eq. 13
# Construct fused labels via Eq. 14
# Generate collapsed labels via multinomial sampling
# Apply Coherence Mechanism for final multi-granularity labels via Eq. 15
for each sample in do
# Compute prediction
# Update model parameters via fused label
end for
end for
Considering that MgEL uses exponential cosine similarity (Eq. 8) to measure sample similarity in the latent feature space, we have aligned the classifier architecture accordingly. Instead of adding a fully connected layer to the backbone network for classification, we employ a cosine classifier to directly classify the features, which ensures better alignment with the feature space's geometry and optimization direction, as cosine similarity is more suitable for high-dimensional feature manifolds.
It is important to emphasize that the proposed MgEL framework operates exclusively during the training phase. It acts as a robust label correction strategy by adjusting supervisory signals based on latent-space evidence fusion. Consequently, the inference pipeline remains entirely unaltered—both structurally and computationally. MgEL introduces no additional latency, memory, or computational overhead at deployment time. The final diagnostic model inherits its real-time performance characteristics solely from the underlying backbone architecture, making MgEL fully compatible with industrial runtime constraints.
To thoroughly evaluate the performance of MgEL, we conducted a series of experiments on three benchmark datasets for bearing fault diagnosis: Single [44], Multiple [43], and Damage [40]. These datasets consist of vibration signals collected directly from mechanical systems during operation, covering various working conditions, rotational speeds, and load conditions. These datasets were selected to represent a wide range of fault scenarios and complexities, ensuring that MgEL can handle diverse real-world conditions effectively.
| Parameter | Detailed information about three datasets | ||
|---|---|---|---|
| Single | Multiple | Damage | |
| No. of categories | |||
| Fault location | Inner, Outer, Ball, Inner and Outer, Inner and Ball, Outer and Ball | ||
| Damage degree | 0.3 mm | 0.3 mm | 0.2, 0.4, 0.6, and 0.8 mm |
| rpm | rpm | ||
| Motor speed | rpm | rpm | rpm |
| rpm | rpm | ||
| Motor load | 0.0, 0.1, 0.2 and 0.3 NM | 0.0 and 0.3 NM | 0.0 and 0.3 NM |
| Sampling frequency | 12 kHz | 12 kHz | 16 kHz |
| No. of tra. samples | 4032 | 46452 | 34100 |
| No. of val. samples | 924 | 10290 | 7600 |
| No. of tes. samples | 4032 | 46452 | 34100 |
Table 2 summarizes the details of each dataset, including fault categories, operating conditions, and the number of samples. Notably, the datasets were chosen without addressing class imbalance, ensuring that the number of training and testing samples for each class is roughly equal. Each sample consists of 2048 continuous data points, with no overlap between any two samples, ensuring a clean and consistent evaluation framework.
With the goal of conducting a comprehensive evaluation of MgEL under various noise environments, two types of noise were introduced: class-dependent asymmetric noise and class-independent symmetric noise. Asymmetric noise was introduced by swapping labels between similar classes at five different intensity levels (). For example, in the Damage dataset, severity labels within the same fault category were swapped, such as replacing the "0.2 mm" label with "0.4 mm" or swapping "0.8 mm" and "0.6 mm". This type of noise simulates realistic scenarios in which label errors occur within similar categories. Symmetric noise was introduced by randomly replacing the original labels with labels from other categories, with five different noise intensities applied ().
To ensure a fair comparison and reproducibility, we adopt MgNet [43], an open-source fault diagnosis architecture released alongside the Multiple dataset and well-suited for time-series analysis in industrial scenarios, as the backbone for evaluating the performance of MgEL. All models were trained using the AdamW optimizer, with momentum coefficients , , and weight decay . The learning rate follows a CosineAnnealing schedule, with the initial value scaled as , ensuring consistency across different training scales. Training is performed for 100 epochs, including a 5-epoch warm-up stage, during which only standard supervised learning is applied, without any additional label correction operations.
All experiments were conducted on an NVIDIA A100 GPU using PyTorch version 2.1.1+cu118. To eliminate the influence of random initialization and stochastic variation, each experiment was repeated at least ten times, with the detailed evaluation results and corresponding analyses presented in the following subsections.
| Datasets | Methods | Accuracy(%) under asymmetric noise | Accuracy(%) under symmetric noise | Mean | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (%) | ||||||||||||
| Single | Baseline | 87.935.51 | 83.164.79 | 75.881.97 | 69.423.47 | 59.260.10 | 68.124.96 | 58.046.44 | 45.605.87 | 29.049.35 | 5.373.79 | 58.18 |
| SL (2019) | 95.800.42 | 86.353.15 | 85.617.28 | 72.603.34 | 61.061.38 | 81.666.66 | 73.148.38 | 58.991.20 | 25.315.43 | 3.381.35 | 64.39 | |
| JoCoR (2020) | 88.510.17 | 89.717.14 | 81.808.32 | 73.874.63 | 60.440.81 | 79.372.00 | 63.385.80 | 53.364.41 | 34.431.30 | 7.421.62 | 63.23 | |
| JNPL (2021) | 64.669.98 | 54.913.24 | 54.224.37 | 36.957.29 | 43.464.35 | 28.807.35 | 29.215.07 | 27.981.28 | 21.739.13 | 8.864.39 | 37.08 | |
| NCR (2022) | 97.541.54 | 90.093.63 | 86.096.91 | 81.732.12 | 75.116.49 | 84.251.31 | 76.595.17 | 68.977.78 | 49.632.68 | 5.030.38 | 71.50 | |
| ALFs (2023) | 89.167.78 | 88.087.80 | 83.602.93 | 69.471.07 | 59.245.62 | 90.680.47 | 86.872.08 | 73.942.46 | 53.652.96 | 5.112.26 | 69.98 | |
| LSL (2024) | 96.243.03 | 95.284.32 | 94.733.82 | 82.566.03 | 70.149.81 | 95.333.98 | 93.340.57 | 82.309.58 | 64.833.16 | 6.733.39 | 78.15 | |
| ANNE (2025) | 91.107.84 | 89.328.27 | 83.791.22 | 75.155.49 | 69.507.78 | 98.741.21 | 97.431.57 | 95.470.57 | 73.178.33 | 4.441.13 | 77.81 | |
| MgEF (Ours) | 99.490.38 | 99.190.35 | 99.090.63 | 96.062.58 | 80.894.69 | 99.550.17 | 98.920.77 | 98.250.41 | 80.463.19 | 23.022.53 | 87.49 | |
| Multiple | Baseline | 75.073.78 | 69.213.16 | 64.113.13 | 55.040.27 | 51.490.92 | 53.002.29 | 48.361.99 | 36.363.22 | 23.030.44 | 7.390.69 | 48.31 |
| SL (2019) | 80.401.85 | 75.520.43 | 71.802.82 | 53.571.73 | 49.670.84 | 72.561.22 | 62.512.54 | 58.292.29 | 34.382.62 | 9.340.53 | 56.80 | |
| JoCoR (2020) | 88.471.14 | 88.700.68 | 87.311.53 | 72.504.18 | 64.881.23 | 74.133.67 | 66.380.98 | 49.362.57 | 31.641.03 | 9.971.43 | 63.33 | |
| JNPL (2021) | 63.590.24 | 63.450.19 | 61.661.21 | 60.121.02 | 55.931.67 | 50.450.33 | 41.542.07 | 33.781.27 | 23.241.28 | 9.571.37 | 46.33 | |
| NCR (2022) | 90.250.57 | 89.340.26 | 86.661.72 | 82.490.85 | 69.891.48 | 66.503.83 | 55.602.50 | 43.011.53 | 26.523.07 | 9.071.69 | 61.93 | |
| ALFs (2023) | 77.041.50 | 73.961.75 | 68.020.74 | 64.003.36 | 54.591.65 | 65.272.76 | 52.350.61 | 32.910.69 | 22.920.73 | 8.401.39 | 51.95 | |
| LSL (2024) | 64.061.57 | 62.434.91 | 66.191.33 | 59.881.83 | 55.320.07 | 47.670.83 | 42.582.20 | 34.911.08 | 24.051.66 | 8.720.99 | 46.58 | |
| ANNE (2025) | 65.552.49 | 67.692.57 | 63.461.44 | 63.601.34 | 57.801.04 | 52.882.58 | 51.154.12 | 39.904.36 | 23.581.72 | 11.100.51 | 49.67 | |
| MgEF (Ours) | 89.330.52 | 89.160.87 | 87.701.15 | 86.200.51 | 75.651.50 | 86.201.28 | 83.491.16 | 81.450.52 | 75.461.80 | 43.185.46 | 79.78 | |
| Damage | Baseline | 91.180.17 | 86.311.18 | 82.381.10 | 67.283.45 | 54.572.16 | 88.780.48 | 84.661.02 | 76.720.30 | 55.241.62 | 20.183.84 | 70.73 |
| SL (2019) | 93.830.42 | 90.532.13 | 88.041.00 | 75.704.60 | 57.450.45 | 94.550.17 | 92.510.19 | 87.881.48 | 76.111.50 | 20.861.74 | 77.74 | |
| JoCoR (2020) | 93.840.19 | 89.221.72 | 85.280.81 | 70.003.85 | 56.661.52 | 91.780.64 | 88.941.25 | 83.641.32 | 62.571.67 | 22.412.13 | 74.43 | |
| JNPL (2021) | 90.180.05 | 86.100.51 | 81.110.99 | 69.620.76 | 57.321.66 | 87.560.93 | 84.950.34 | 76.172.60 | 52.134.56 | 24.302.23 | 70.94 | |
| NCR (2022) | 94.720.64 | 92.000.30 | 86.241.44 | 75.712.07 | 61.991.99 | 91.750.77 | 89.442.55 | 83.490.74 | 61.450.75 | 18.201.09 | 75.50 | |
| ALFs (2023) | 96.930.62 | 94.961.41 | 90.112.67 | 78.452.18 | 59.090.83 | 96.030.62 | 94.011.71 | 87.322.06 | 62.740.85 | 19.771.66 | 77.94 | |
| LSL (2024) | 90.090.84 | 86.560.44 | 81.670.99 | 70.830.72 | 57.551.07 | 86.761.06 | 83.611.56 | 75.461.08 | 54.414.17 | 20.281.20 | 70.72 | |
| ANNE (2025) | 96.630.18 | 96.500.23 | 92.750.31 | 87.080.45 | 64.416.91 | 97.360.65 | 96.990.26 | 90.410.41 | 83.423.21 | 33.668.18 | 83.92 | |
| MgEF (Ours) | 97.480.42 | 97.190.45 | 96.700.87 | 93.250.65 | 75.031.01 | 97.310.22 | 96.470.34 | 95.810.27 | 94.310.35 | 75.072.35 | 91.86 | |
To evaluate the effectiveness of the proposed MgEL framework, we conducted comprehensive comparisons with seven state-of-the-art LNL approaches: SL (2019) [30], JoCoR (2020) [33], JNPL (2021) [45], NCR (2022) [46], ALFs (2023) [27], LSL (2024) [16], and ANNE (2025) [47], across three datasets with varying types and intensities of label noise. We visualize the performance comparison in Figure 5 and provide the detailed results in Table 3, where bold values represent the best accuracy achieved by other methods under each noise setting, facilitating an intuitive comparison with MgEL.
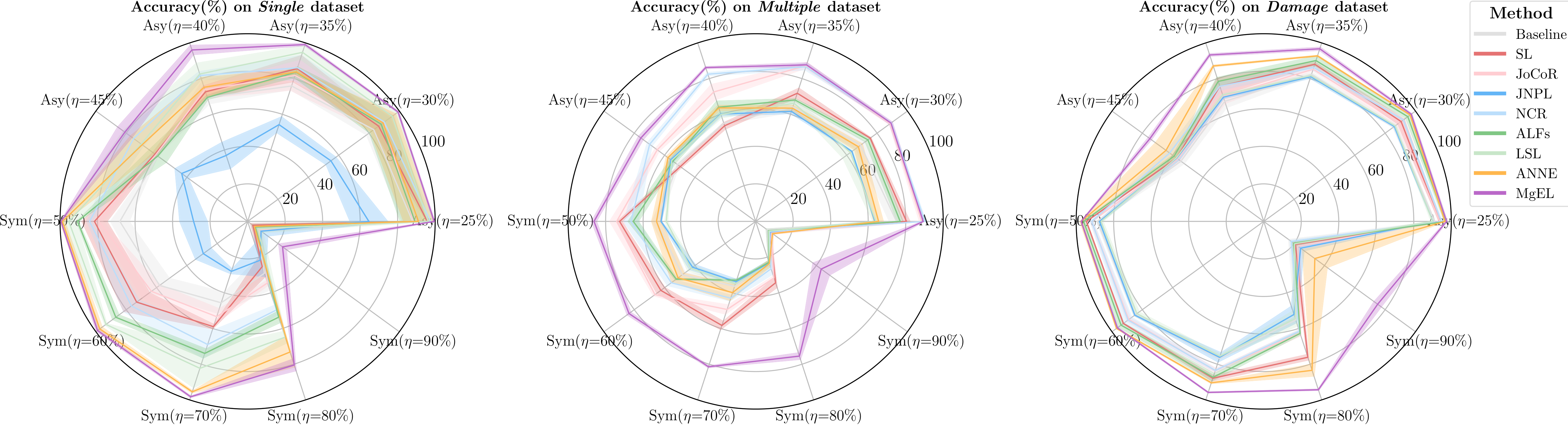
Overall, MgEL consistently outperforms all competing approaches across different datasets and noise scenarios, demonstrating superior robustness and generalization even in the presence of severe label corruption. On the Single dataset, MgEL achieves a mean accuracy of 87.49%, surpassing the strongest baseline (LSL, 78.15%) by 9.34%. This advantage is amplified further under high symmetric noise (), where MgEL maintains a robust 23.02% accuracy compared to 7.42% for JoCoR. A similar pattern is observed on the Multiple dataset, where MgEL yields an average accuracy of 79.78%, outperforming the second-best baseline (JoCoR) by 16.45%. On the more challenging Damage dataset, MgEL delivers the highest performance (91.86%), surpassing ANNE (83.92%) by 7.94%.
These consistent improvements across datasets and noise conditions are attributed to several technical innovations in MgEL. One key reason is that, instead of relying on heuristic sample selection or loss-based reweighting, MgEL constructs a quantum-inspired superposition state for each sample by aggregating local observations from entangled feature clusters. This formulation captures class attribution uncertainty with greater fidelity. Additionally, MgEL fuses the pseudo-label and original annotation via an evidence-aware belief mass , derived from the distribution of cluster-level statistics. This enables adaptive weighting of conflicting information sources based on their consistency. Moreover, the Coherence mechanism safeguards against early confirmation bias by retaining the superposition state whenever the pseudo, annotation, and collapsed labels fail to reach consensus, postponing hard commitments until sufficient evidence accumulates in later training iterations.
The performance advantage of MgEL becomes especially prominent under high-noise symmetric settings, indicating its tolerance against purely stochastic label perturbations that often mislead traditional LNL strategies. Moreover, its stability across diverse datasets highlights its generalizability and scalability for real-world fault diagnosis tasks.
To further investigate the source of MgEL's effectiveness, we conduct an ablation study by selectively removing each of its three core components: Entanglement, Evidence, and Coherence. The results are summarized in Table 4 and visualized in Figure 6.
| Methods | Entanglement | Evidence | Coherence | Average accuracy(%) | ||
| Single | Multiple | Damage | ||||
| Baseline | 58.18 | 48.31 | 70.43 | |||
| A1 | 85.64 | 76.89 | 90.22 | |||
| A2 | 84.61 | 75.58 | 89.12 | |||
| A3 | 82.09 | 72.95 | 87.74 | |||
| A4 | 79.41 | 70.16 | 86.09 | |||
| A5 | 81.62 | 72.33 | 87.67 | |||
| A6 | 83.88 | 74.34 | 88.78 | |||
| MgEL | 87.49 | 79.78 | 91.86 | |||
Taken together, Table 4 and Figure 6 show that the full MgEL framework, which integrates all three components, achieves the highest accuracy across all datasets. Removing any component consistently leads to a decline in performance, indicating that the effectiveness of MgEL stems from the complementary roles of entanglement-based pseudo-source modeling, evidence-aware label fusion, and coherence-guided filtering.
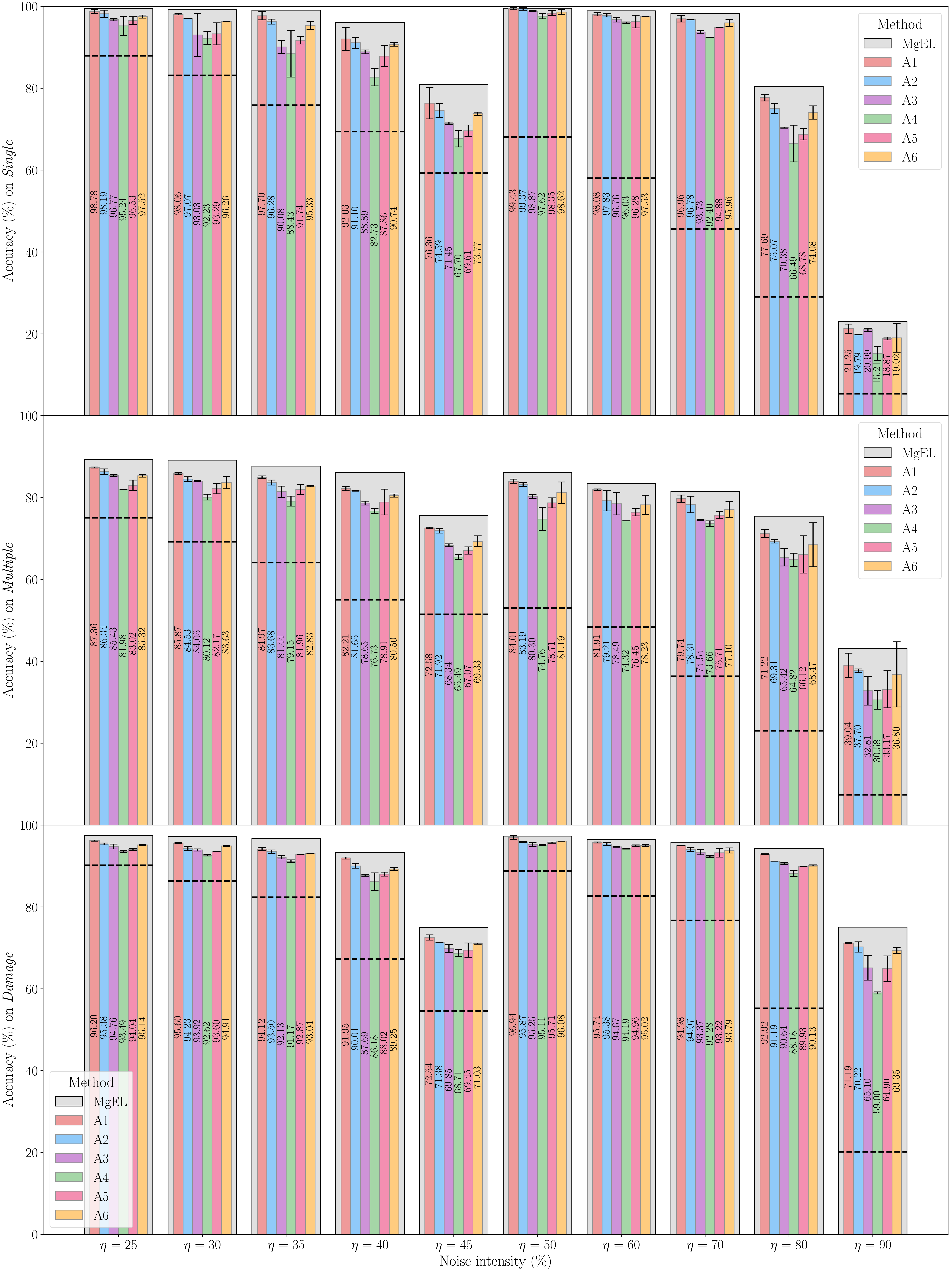
The effect of removing Entanglement is evident when comparing configurations A1 and A4 to the full model. A1, which disables Entanglement while retaining Evidence and Coherence, shows a performance decline (e.g., 76.89% 79.78% on Multiple). The degradation becomes more pronounced in A4, where only Entanglement is active, leading to further reductions in accuracy (e.g., 70.16%). These trends suggest that Entanglement is critical for constructing reliable pseudo-source representations. Its role in partitioning the feature space introduces stochastic diversity in cluster formation, capturing the distributional uncertainty of class attribution through superposition states, which is essential for robust label inference.

The role of Evidence is assessed by examining A2 and A5, both of which remove this component. A2 maintains Entanglement and Coherence but excludes Evidence, resulting in performance drops across all datasets (e.g., 75.58% 79.78% on Multiple). A5, retaining only Entanglement, performs even worse. These observations indicate that while structural diversity is necessary, accurate fusion of annotations and pseudo-labels requires confidence calibration. The belief mass , computed from local similarity-weighted label distributions and adjusted for noise intensity, serves this purpose. Its removal forces reliance on raw class probabilities, weakening the model's ability to distinguish reliable label sources. Thus, Evidence enhances label consistency by integrating supervision signals based on their reliability within the cluster context.
The effect of Coherence is reflected in A3 and A6. A3 excludes Coherence while preserving Entanglement and Evidence, leading to a modest performance reduction (e.g., 72.95% 79.78% on Multiple), while A6—disabling both Coherence and Entanglement—shows the lowest performance among all variants. These results confirm that Coherence plays a significant role in label stability, especially under ambiguous or conflicting supervision. The mechanism selectively defers label commitments by reverting to the superposition state when the pseudo, annotation, and collapsed labels do not agree. Therefore, Coherence mitigates confirmation bias and stabilizes predictions by withholding unreliable updates in the presence of low label consensus.
Collectively, the ablation results demonstrate that MgEL's tolerance to noisy labels comes from the interplay of three complementary mechanisms: entanglement introduces structured diversity for uncertainty modeling, evidence enables reliability-aware label fusion via belief-based weighting, and coherence mitigates confirmation bias by deferring low-consensus decisions. Their unified integration equips MgEL with robust generalization capabilities across diverse and corrupted learning environments.
To empirically support Assumption 1, we visualize the t-SNE embeddings of both training and test samples from the three datasets under 90% symmetric noise, as shown in Figure 7. The resulting projections reveal significant differences in the topological organization of feature manifolds, providing intuitive evidence of noise-induced structural perturbations and highlighting MgEL's ability to counteract these distortions through more coherent class representations.
Compared to the baseline, the latent features learned by MgEL show significantly improved intra-class compactness and inter-class separability. On the Single dataset, clear and well-separated clusters emerge even for complex fault types, while the baseline features remain entangled with indistinct boundaries. The Multiple dataset, which introduces greater domain and fault variability, further demonstrates MgEL's robustness: despite the increased difficulty, MgEL preserves coherent topological structures for most classes, while the baseline embeddings collapse into ambiguous, overlapping manifolds.
Notably, the effect is most pronounced on the Damage dataset, which consists of 49 fine-grained fault categories and extreme label corruption (). In this challenging setting, the baseline model fails to preserve class-discriminative geometry, leading to severe semantic drift. In contrast, MgEL successfully induces structured manifolds with meaningful class-wise alignment, consistent with the suppression of structural perturbations predicted by the theoretical model.
Furthermore, training embeddings offer additional insight into MgEL's manifold-regularizing behavior. Although residual intra-cluster variance persists due to corrupted supervision, the global alignment between training and test distributions is significantly improved under MgEL. This suggests that the framework filters noise at the label level and stabilizes representation learning by regularizing optimization trajectories.
The observed improvements are attributed to MgEL's evidence-aware label construction process, which incorporates uncertainty through probabilistic superposition and belief-based fusion mechanisms. These mechanisms effectively mitigate the propagation of biased gradients and restore the semantic coherence of the latent space.
Taken together, the t-SNE results corroborate the theoretical analysis in Assumption 1, showing that extreme label noise induces a representation-level structural shift. MgEL mitigates this phenomenon by preserving class-consistent manifolds in the latent space, improving both robustness and generalization.
Motivated by the challenge of confirmation bias in LNL, this work proposes MgEL, a quantum-inspired framework that introduces a novel multi-granularity evidence labeling mechanism by simulating the observation–collapse behavior of entangled systems. Through pseudo-source construction, evidence-aware fusion, and coherence-guided filtering, MgEL effectively integrates annotations, pseudo-labels, and collapsed labels to create robust supervision signals. Extensive experiments across three fault diagnosis benchmarks confirm that MgEL outperforms existing methods in most scenarios, particularly under severe symmetric noise, while consistently improving the quality of latent representations. MgEL provides a theoretically grounded and practically scalable solution for trustworthy fault diagnosis in data-driven industrial systems. Beyond its empirical success, MgEL introduces a principled information fusion strategy that integrates multiple uncertain label sources, offering new insights into uncertainty modeling and decision-level fusion in noisy environments.
Despite its promising performance, MgEL has several limitations. The stochastic nature of random partitioning may cause instability in small or highly imbalanced datasets, and reliance on similarity-based neighborhood construction can be sensitive to feature distortions during early training. Future research could explore more robust entanglement schemes, incorporate adaptive clustering, or integrate causal and temporal priors into the label-fusion process. Moreover, extending the proposed framework to semi-supervised, active, or federated learning settings holds promise for advancing both the theory and practice of information fusion under uncertainty.
 Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. Chinese Journal of Information Fusion
ISSN: 2998-3371 (Online) | ISSN: 2998-3363 (Print)
Email: [email protected]

Portico
All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/