1. Introduction

Multi-Target Tracking (MTT) serves as a critical technique in radar, sonar and other surveillance systems [1, 2], with recent advances spanning deep learning-based trajectory analysis [3], multi-sensor fusion frameworks [4], and graph-based feature representation [5]. The main challenge of MTT lies in effectively resolving the data association problem between targets and collected measurements. There are two traditional MTT methods: the multiple hypothesis tracking (MHT) filter [6, 7] and the joint probabilistic data association (JPDA) filter [8]. While MHT theoretically achieves near-optimal solutions by maintaining multiple association hypotheses over time, its computational complexity grows exponentially with the number of targets and measurements due to the combinatorial hypothesis space. This makes it challenging for real-time applications without aggressive pruning and approximation techniques. In comparison, JPDA reduces computational burden through probabilistic weighting of association hypotheses. However, it suffers from two inherent limitations: (1) it assumes a fixed and known number of targets during tracking; and (2) it is prone to track coalescence in dense target environments.

The joint integrated probabilistic data association (JIPDA) filter [9] plays a critical role in information fusion for multi-target tracking by integrating measurement data from different sensors and targets. It extends the concept of target existence probability, enabling joint estimation of data associations and target existence states while efficiently handling the fusion of probabilistic information. JIPDA evaluates feasible measurement-to-track association hypotheses, fuses their probabilistic weights, and updates both target existence probabilities and state estimates. By dynamically terminating tracks with low existence probabilities (e.g., below a threshold), this probabilistic framework allows JIPDA to adapt to scenarios where the number of targets varies over time. However, the JIPDA filter remains susceptible to the track coalescence problem. This occurs when targets are in close proximity, leading to overlapping tracking gates and ambiguous data associations. As a result, measurements from different targets may be incorrectly weighted, biasing state estimates. Prolonged proximity can cause merged tracks that cannot be distinguished, even after targets are separated. This limitation is particularly problematic in dense target scenarios and restricts the practical effectiveness of JIPDA.

To address the issue of track coalescence caused by overlapping validation gates and the resultant association uncertainty problem, we propose an adaptive particle swarm optimization-based joint integrated probabilistic data association (PSO-JIPDA) filter. By optimizing the posterior association probabilities, the proposed method overcomes the tracks coalescence problem. This geometric constraint induces two critical issues: (1) substantial ambiguity in measurement-to-track association; and (2) pronounced multimodal characteristics in the posterior density function. Specifically, during state estimation, measurements originating from distinct targets may be erroneously associated with the same track, leading to a marked increase in the trace of the state estimation covariance matrix (established research has demonstrated this metric as an effective quantitative measure of posterior distribution multimodality [10, 11]). For enhanced accuracy in multi-target state estimation, the PSO approach is used to optimize the posterior probability density and minimize the trace of the covariance matrix. PSO operates through the following sequential implementation steps: First, in the initialization phase, particle positions are randomly generated within the solution space. These position vectors, whose dimensionality equals the problem's free parameters, represent possible solutions. Initial positions and velocities are randomly generated for all particles to ensure uniform distribution across the search space. Position coordinates are typically bounded within predefined ranges to comprehensively cover feasible regions. Each particle evaluates its fitness value through a predefined objective function, quantifying the quality of its current solution. During iterative updates, particles dynamically adjust their states by tracking two critical extremum values: the personal best, denoting the optimal solution discovered by an individual particle, and the global best, representing the best solution identified by the entire swarm. The particle state update mechanism combines three components: inertial momentum, cognitive learning (based on individual historical performance), and social learning (guided by swarm collaboration). A velocity vector adjusts the particle's movement direction and step size, while position updates translate these velocities into spatial displacements. Additionally, we have implemented several improvements to the PSO algorithm, including optimization of the inertia weight adjustment strategy and enhancements to the particle position update method, among others. These modifications will be elaborated in detail in Section 4. To summarize, our contributions are threefold as follows.

The remainder of the paper is structured as follows. Section 2 introduces the proposed PSO-JIPDA algorithm, detailing the utilization of PSO for posterior density optimization and providing concrete implementation examples. Section 3 validates the effectiveness of our method through experiments in two distinct scenarios. Section 4 draws conclusions.

2. Related Work

To address track coalescence in multi-target tracking, various data association techniques have been innovated. The exact nearest neighbor JPDA (ENNJPDA) filter [12] represents an early approach, reducing computational complexity by aggressively pruning all but the highest-probability association hypothesis. However, this method presents significant susceptibility to both false alarms and missed detections, as it discards potentially useful alternative hypotheses. To address these limitations, the JPDA* variant [13] was introduced, refining the hypothesis selection process through selective pruning: it retains the most consistent data association hypothesis to compute measurement-to-target assignment probabilities, balancing computational efficiency with robustness. Building on this foundation, The JIPDA* filter [14] integrates the JIPDA framework with JPDA*, creating a more resilient solution for track coalescence scenarios. JIPDA* operates by prioritizing a single optimal association hypothesis from the set of possible track-measurement associations, pruning alternative hypotheses that involve identical tracks and measurements but differ in assignments. By eliminating competing hypotheses that could induce trajectory merging or misassignment, JIPDA* maintains coherent state estimation even in cluttered environments where traditional JPDA-based methods often fail to resolve ambiguous interactions. However, the discarded hypotheses might contain residual data association information that could potentially enhance the accuracy of tracking, despite being suboptimal in the current selection framework. To address this problem, our recent research [15] introduces the evolutionary optimization-based joint integrated probabilistic data association (EOJIPDA) method. EOJIPDA operates by probabilistically integrating all feasible association hypotheses through posterior density optimization. This mechanism preserves the probabilistic significance of primary and secondary hypotheses events, ensuring comprehensive utilization of measurement information. Nevertheless, the integration of evolutionary computation inherently increases the algorithm's computational load.

Aforementioned methods rely on data association mechanisms, and there is another class of methods based on the finite set statistics (FISST) [16]. Notable implementations include the probability hypothesis density (PHD) filter [17], its cardinality-enhanced variant CPHD [18], and the multi-Bernoulli (MB) formulation [19]. Subsequent refinements have produced labeled variants such as labeled multi-Bernoulli [20] and generalized label multi-Bernoulli filters [21, 22], all using the random finite set (RFS) theory for systematic uncertainty modeling. The PHD and CPHD techniques use moment approximations to circumvent the computational intractability inherent in full Bayesian multi-target posterior density calculations. Different from this paradigm, the MB approach parameterizes multi-Bernoulli RFS components rather than maintaining explicit density representations. Labeled extensions, such as LMB and GLMB, enable target identity preservation. These FISST-based methods avoid explicit combinatorial association by implicitly modeling multi-target states as sets, offering a principled mathematical framework for MTT.

3. Background

4. Methodology

4.2 Particle Swarm Optimization of the Posterior Density

For posterior density optimization, target permutations across distinct association hypotheses are reconfigured to minimize the cost function defined in (1). The optimization is effectuated by means of PSO [5], with the principal procedures of the PSO-JIPDA approach as follows.

Step 1: PSO setup for the optimization of the posterior density.

For PSO implementation, we adopt (1) as the global fitness function. The solution space comprises every permutation of the current target indices and is defined as:

$$𝒫=\{{\Pi }_h\mid h=1,\dots N_{\mathscr{H}}\}$$

where ${\Pi }_h$ denotes the permutation set corresponding to the $h$th association hypothesis and ${\Pi }_h$ has cardinality $\left|{\Pi }_h\right|=n_k!.$ We initialize a PSO swarm with $N_p$ particles. At time $k$, the position $x_p^k$ of each particle $p$ represents a candidate solution vector, where each element corresponds to the index (from 1 to $n_k$) of a specific target permutation chosen for a particular hypothesis. The goal is to find the vector of permutation indices (one index per hypothesis) that optimizes a global fitness function.

Step 2: PSO Iterative Optimization.

Execute the PSO algorithm for defined generations and update the inertia weight $w$ at time $k$. In each generation, for a particle, we perform the following steps.

First, compute the inertia weight. The original linear decreasing inertia weight strategy was enhanced with a nonlinear adaptive approach. The dynamic inertia weight is calculated based on the iteration progress and fitness values, as follows

where $w_{\max }$ and $w_{\min }$ represent the maximum and minimum inertia weights, respectively; $f(\cdot )$ denotes fitness function; $f_{\text{current}}$, $f_{\text{mean}}$, and $f_{\min }$ denote the current fitness function, the mean fitness function and the minimum fitness function, respectively.

Figure 1 Flowchart of PSO-JIPDA algorithm.

Second, update each particle's velocity $v_p^k$ using the inertia weight $w$ which controls how much the particle's previous velocity affects its current movement direction. Then, update each particle's position vector $x_p^k$ using the obtained velocity, guiding the search towards better permutation index vectors. The mathematical description of the update process is as follows:

$${\nu }_p^{k+1}=w{\nu }_p^k+c_1{r}_1\left(p_{best}-x_p^k\right)+c_2{r}_2\left(g_{best}-x_p^k\right)$$

$$x_p^{k+1}=x_p^k+{\nu }_p^{k+1}$$

where $c_1$ is the individual learning factor determining the influence of the particle's own best position $p_{\text{best}}$ on its velocity update; $c_2$ is the social learning factor reflecting the impact of the global best position $g_{\text{best}}$ found by the entire swarm on the particle's velocity update; $r_1\sim 𝒰(0,1)$ is the individual stochastic factor; $r_2\sim 𝒰(0,1)$ is the social stochastic factor; $p_{\text{best}}$ is the best position that the particle has reached so far in the search process; $g_{\text{best}}$ is the best position found by the entire particle swarm so far. Note that the boundary handling is used internally as particle positions correspond to discrete indices.

Third, evaluate the fitness of each particle using each particle's position vector $x_p^k$ and update each particle's personal best $p_{\text{best}}$ position and swarm's global best $g_{\text{best}}$ position based on fitness values, as follows:

Step 3: Apply Optimal Permutations.

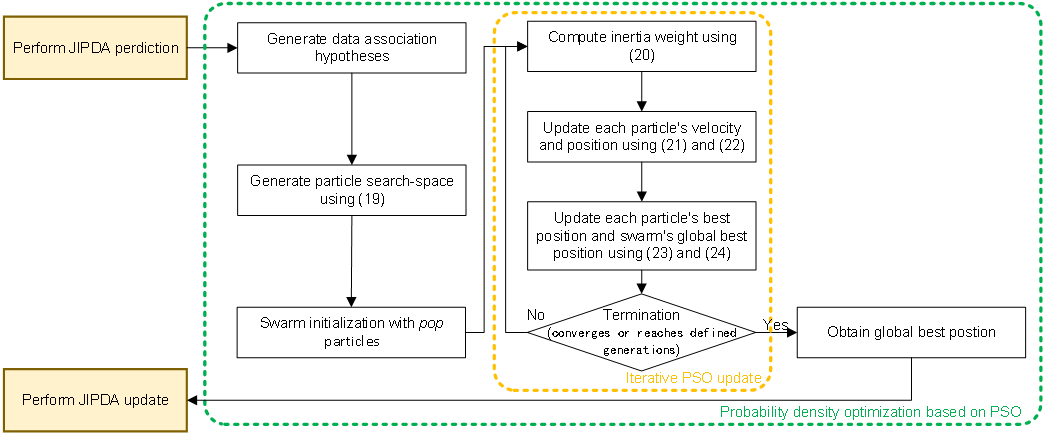
After PSO converges or reaches defined generations, retrieve the global best position vector $g_{\text{best}}$. For each hypothesis in $g_{\text{best}}$, reorder the corresponding hypothesis-specific index. Subsequently, the standard JPDA hypothesis-weighted marginalization (15)-(17) performed to estimate the target state estimate $x_{t,k}$, the covariance matrix $P_{t,k}$, and the existence probability $P_s(t,k)$. Figure 1 shows the flowchart of the proposed PSO-JIPDA algorithm. The probability density optimization procedure is enclosed in the dotted green box, while the iterative PSO update is shown in the dotted orange box. The "Termination" module determines whether the optimization process should end. If not terminated, the process returns to the "iterative PSO update" stage. If terminated, it outputs the global best position.

4.3 Illustrative Example

To illustrate the PSO-JIPDA algorithm's operational process, we consider a simplified one-dimensional case with two Gaussian-distributed targets generating two measurements. Assume two association hypothesis events ${\psi }_1$ and ${\psi }_2$ are established, with density of target $t$ under hypothesis ${\psi }_h$ is modeled as $p^{t|h}\left(x\right)=\{r^{t|h},𝒩(x^{t|h},p^{t|h})\}$. The initial posterior density is specified by

Based on (15)-(17), the Gaussian-approximated probability density for each target is characterized as

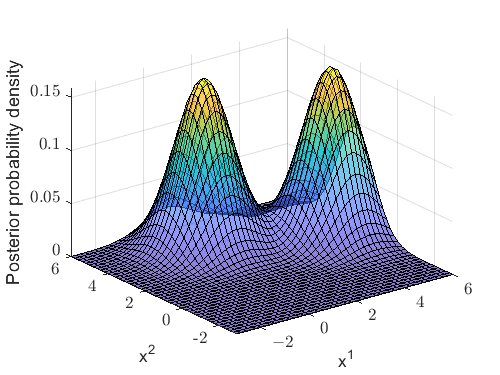
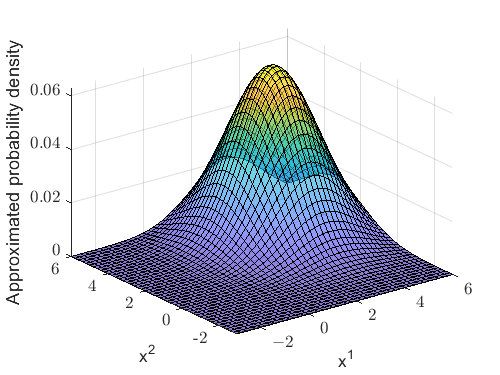
Figure 2(a) and 2(b) present the posterior probability density of the joint track state and its Gaussian approximation, respectively. It can be observed that a considerable difference exists between these two densities, demonstrating the limited precision of the Gaussian approximation. In this case, the trace of the covariance matrix is

$$C_0=2.25+2.80=5.05$$

which can be computed using (1).

(a)

(b)

Figure 2 (a) Posterior and (b) approximated probability densities at iteration 0.

The posterior probability density is then optimized using the particle swarm optimization (PSO) algorithm. Following five iterations, the final optimized result is derived as follows:

${\psi }_1:\{\begin{array}{c}{p}^{11}\left(x\right)=\{0.4,N(1,1)\}\\ p^{2|1}\left(x\right)=\{0.1,N(5,1)\}\end{array}$

derived as follows

${\psi }_2:\{\begin{array}{c}{p}^{1|2}\left(x\right)=\{0.5,N(2.3,1)\}\\ p^{2|2}\left(x\right)=\{0.5,N(4,1)\}\end{array}$

Using (15)-(17), the approximated probability density for each track is given as

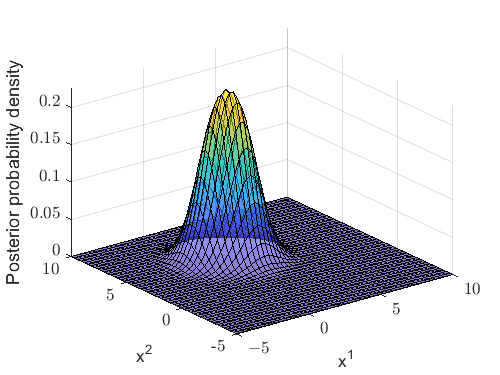
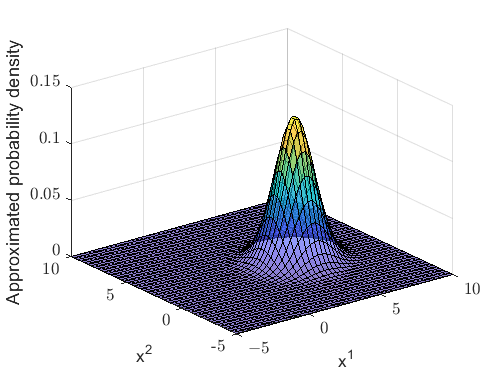
Figure 3(a) displays the initial posterior probability density, while its approximated single Gaussian density is presented in Figure 3(b). Obviously, Figures 3(a) and 3(b) demonstrate a strong correlation, whereas Figures 2(a) and 2(b) exhibit a notable divergence. In this case, the trace of the covariance matrix is

$$C_0=1.25+1.23=2.48$$

After PSO optimization, the trace decreases by 50.89% relative to the initial trace (9), demonstrating a significant improvement in Gaussian approximation and state estimation precision. These statistical analyses exhibit strong concordance with theoretical expectations.

(a)

(b)

Figure 3 (a) Posterior and (b) approximated probability densities at iteration 5.

5. Experiments

We assess the PSO-JIPDA filter's efficacy in a complex 2D multi-target tracking environment, employing kinematic modeling of moving targets with

where ${[p_x^k,p_y^k]}^T$ denotes the target position and ${[v_x^k,v_y^k]}^T$ is the target velocity. The transition matrix of the motion model is

where $\otimes$ denotes the Kroneker product, $I_2$ represents a $2\times 2$ identity matrix, and $T_S$ indicates sampling interval. The process noise $u_k$ follows a Gaussian distribution with covariance matrix

where $q$ is a tuning parameter. A sensor collects target measurements within the monitoring region in both experimental scenarios. For simplicity, it is assumed that the sensor only captures target position information. Therefore, the observation matrix of the measurement model is

The covariance of the Gaussian measurement noise ${𝐰}_k$ is

where ${\sigma }_x$ is the standard deviations of the measurement noise in $x$ coordinate and ${\sigma }_y$ is the standard deviations of the measurement noise in $y$ coordinates, respectively.

The sensor operates at a fixed sampling interval of $T_s=1\text{s}$, with a detection probability of $P_D=0.92$. A gating threshold of $\gamma =9.21$[25] is applied, corresponding to a two-dimensional gating probability of $P_W=0.99$. The Markov chain model coefficients in (6) are the same as [9], with $p_{11}=0.98$ and $p_{21}=0$. Track management follows probabilistic rules: tracks are confirmed when the existence probability surpasses $P_C=0.83$, while terminated when falling below $P_T=0.0909$, following the criteria established in [2]. For the PSO algorithm, we use where $w_{\text{max}}=0.9$, $w_{\text{min}}=0.4$, $c_1=2$, and $c_2=2$. We employ the Optimal Sub-Pattern Assignment (OSPA) metric [26], a well-established performance measure in random finite set (RFS) based multi-target tracking [16, 19], to quantitatively evaluate tracking accuracy.

For two sets $X=\{x_1,\dots ,x_n\}$ and $Y=\{y_1,\dots ,y_m\}$ representing true and estimated states (assuming $n\ge m$), the OSPA distance is defined as [26]:

where $d^{\left(c\right)}\left(x_i-y_{\pi \left(i\right)}\right):=\min (c,\Vert x-y\Vert )$, $c>0$ is the cut-off parameter, $p\ge 1$ is an order parameter, and $\pi$ is a permutation function in the set of permutations ${\Pi }_n$; if , $d_{p,c}^{\text{OSPA}}(X,Y)=d_{p,c}^{\text{OSPA}}(Y,X)$. All numerical experiments were conducted using MATLAB R2022b on a computing platform equipped with a 3.40 GHz CPU.

In the surveillance area, two targets follow deterministic trajectories [10, 11], [13] as described in Figure 4. The targets initially maintain parallel motion at close proximity and ultimately they separate. In Figure 4, the parameters are selected as: $\varphi =\pi /3$, $d=100\text{m}$, and $l_1=l_2=1000\text{m}$. Both targets travel at a constant speed $v=100m/s$. The measurement noise is characterized by ${\sigma }_x={\sigma }_y=10\text{m}$.

Figure 4 Simulated scenario 1.

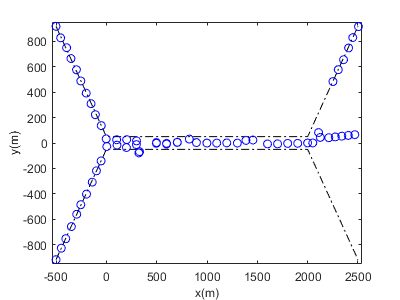
Figure 5(a) and 5(b) present a single-run comparison of the estimated target trajectories obtained from the conventional JIPDA filter and the proposed PSO-JIPDA filter, respectively. When the two targets move in close proximity, the JIPDA filter exhibits severe track coalescence: the estimated trajectories completely overlap, despite their true tracks being distinct. Even after the targets are separated, the JIPDA filter fails to resolve their individual trajectories, leading to persistent estimation errors. In contrast, the PSO-JIPDA filter maintains highly accurate trajectory estimates which closely follow the true tracks. Notably, significantly reduced track coalescence occurs during the targets' proximity stage, and the filter successfully tracks their subsequent separation. This demonstrates that PSO-JIPDA effectively mitigates track coalescence through optimized posterior density handling, achieving superior state estimation.

(a)

(b)

Figure 5 Estimated target trajectories for case 1. The true target trajectories are denoted with black dotted lines and the estimated target trajectories are denoted with dots: (a) JIPDA; (b) PSO-JIPDA.

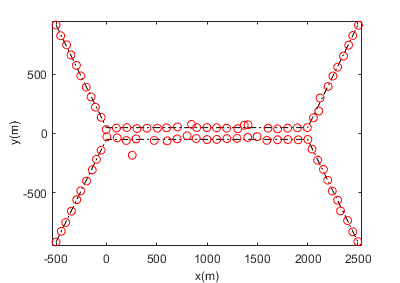
To demonstrate the robustness of our proposed algorithm, we increased the noise to ${\sigma }_x={\sigma }_y=15\text{m}$ and reduced the distance to $d=50\text{m}$ between the two target trajectories. Figure 6(a) clearly illustrates a pronounced track coalescence phenomenon, where the estimated positions of targets merge into a single track when the targets move in close proximity, significantly degrading the tracking performance. In contrast, Figure 6(b) demonstrates the superior capability of the PSO-JIPDA filter, which maintains high-precision state estimation for each individual target even under challenging conditions where targets are closely spaced. By effectively resolving the track coalescence issue, the PSO-JIPDA filter ensures accurate and reliable tracking performance, and these experimental results validate its enhanced robustness compared to the conventional method. The improved performance stems from the optimized posterior probability density enabled by the PSO-JIPDA framework, which successfully prevents track merging while preserving estimation accuracy.

(a)

(b)

Figure 6 Estimated target trajectories for case 2. The true target trajectories are denoted with black dotted lines and the estimated target trajectories are denoted with dots: (a) JIPDA; (b) PSO-JIPDA.

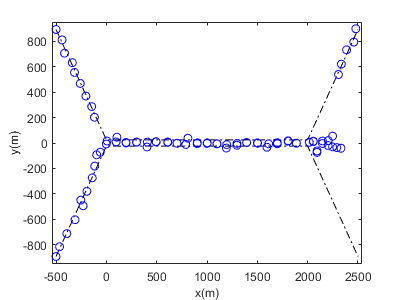
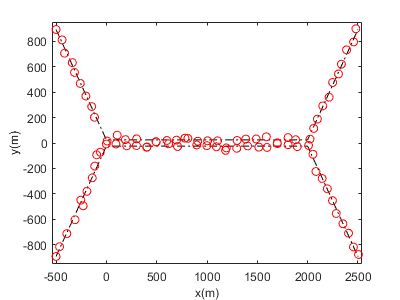
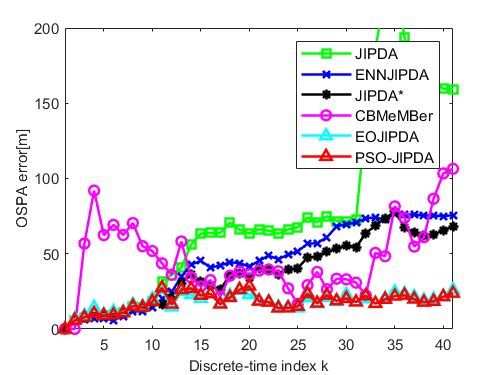
Figure 7 presents a comparative analysis of the average OSPA distance across 100 Monte Carlo experiments for the following algorithms: JIPDA, ENNJIPDA, JIPDA*, CBMeMBer [19], EOJIPDA, and PSO-JIPDA. Experimental results indicate that the JIPDA filter exhibits significantly higher OSPA errors than comparative algorithms caused by the track coalescence problem. Notably, while the ENNJIPDA algorithm was designed to address coalescence, its performance remains highly sensitive to clutter interference and missed detection events. Compared to the JIPDA* filter, the EOJIPDA and PSO-JIPDA filters use the posterior density information more comprehensively and demonstrate superior tracking performance in terms of the OSPA error measure.

Figure 7 Average OSPA distances for scenario 1.

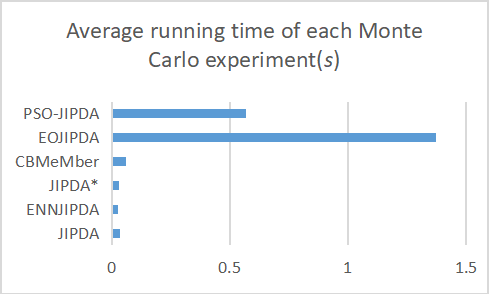
In Figure 8, the average running time of each Monte Carlo simulation for the JIPDA, ENNJIPDA, JIPDA*, CBMeMber, EOJIPDA, and PSO-JIPDA filters is presented, based on 100 Monte Carlo trials. Due to the optimization of the posterior probability density in the PSO-JIPDA algorithm, it incurs a higher computational cost compared to JIPDA, ENNJIPDA, JIPDA*, and CBMeMber. However, the PSO-JIPDA algorithm demonstrates a satisfactory trade-off between tracking performance and computational efficiency. These results suggest that, despite the increased computational time due to the posterior density optimization, the PSO-JIPDA algorithm achieves comparable tracking accuracy and improved runtime performance than the EOJIPDA algorithm, making it a more efficient choice.

Figure 8 Running time comparison of all algorithms.

6. Conclusion

This paper proposes a novel PSO-JIPDA approach designed to effectively address the critical technical challenge of track coalescence prevalent in multi-target tracking systems operating in complex cluttered environments. Through rigorous analysis of limitations inherent in conventional JIPDA filters, this study introduces a novel optimization strategy. The research implements the optimization of the posterior probability density in the classical JIPDA filter using an advanced particle swarm intelligence optimization approach, achieving enhancement in the tracking accuracy.

Future research directions include extending the PSO-JIPDA framework to accommodate nonlinear measurement models, optimizing swarm initialization strategies for real-time applications, and exploring hybrid optimization algorithms to further reduce computational overhead. Additionally, integrating adaptive parameter tuning mechanisms for the PSO coefficients may further enhance the robustness. This work provides a solution for intelligent swarm-based optimization in MTT systems, with potential applications in autonomous surveillance, robotics, and sensor networks.