1. Introduction

The study of nanofluids has gained significant attention due to their enhanced thermal and fluid dynamic properties, making them ideal candidates for various engineering applications such as heat exchangers and cooling systems. The Casson-Williamson nanofluid, a non-Newtonian fluid, exhibits distinct characteristics that are crucial for modelling complex fluid flow and heat transfer phenomena. The addition of nanoparticles improves the thermal conductivity and viscosity of the base fluid, offering better heat transfer capabilities. Understanding the effects of external factors such as magnetic fields, Brownian motion, and thermophoresis on nanofluid flow is essential for optimizing their performance in practical applications. This paper focuses on analysing these effects using an Artificial Neural Network Backpropagation Levenberg-Marquardt (ANN-BLMS) model, which has proven effective for solving nonlinear differential equations governing nanofluid flow.

Chamkha et al. [1] Analytical and numerical tests of rivers of $F{e}_3{O}_4$ water nanofluids were performed at the movable level in the presence of hyper suppression. They investigated how magnetic fields affect the thermal performance and heat transfer of nanofluid systems, demonstrating the improved heat transfer capabilities of nanofluids under these conditions. Pal et al. [2] were enriched into MHD nanofluid-presence via exponential stretching sheets. Her study took into account the presence of gyrotactic microorganisms and thermal radiation. This further confirms the importance of magnetic fields to improve heat and mass transfer into nanofluid systems. Amjad et al. [3] provided a numerical solution to the magnetized Williamson nanofluid river via an exponentially stretchable permeable surface. This study took into account temperature-dependent viscosity and thermal conductivity, and the effects of Brownian motion and thermophoresis examined nanofluid flow and showed an important effect on heat transfer. Srinivasulu et al. [4] investigated the effects of gradient fields on rivers, and heat and mass transfer from Williamson nanofluids via expansion sheets. Their research highlighted the importance of magnetic field effects in controlling flow behavior and improving heat transfer in nanofluids, particularly for industrial applications.

Ghasemi et al. [5] investigated the effects of solar radiation on stagnant point flow of MHD through expansion sheets and heat transfer of nanofluids. Their results showed the combined effects of magnetic field and thermal radiation on nanofluid behavior, providing insight into energy system optimization. Makhdoum et al. [6] analyzed the effects of entropy generation and nanoparticle units on stagnant point flow of nanofluids via stretch sheets. This study has a deeper understanding of the role of entropy generation and nanoparticle units in nanofluid flows, which can have a significant impact on the efficiency of thermal systems. Prasannakumara [7] investigated the heat transport in the Maxwell Nanofluid River via an expansion sheet taking into account the effects of magnetic dipole effects. This study focuses on the interaction between fluid dynamics and heat transfer processes under the influence of magnetic fields, providing valuable insights for optimizing the system in a nanfluid-based system.

Mahmood et al. [8] investigated MHD mixed convective stagnation point flow of nanofluid past a permeable stretching sheet with nanoparticles aggregation and thermal stratification. Their work extended the understanding of nanofluid flow in complex environments, where nanoparticle aggregation and thermal stratification play a significant role in heat transfer and fluid dynamics. Lund et al. [9] analyzed dual solutions and the stability of hybrid nanofluid over a stretching/shrinking sheet executing MHD flow. They focused on the stability of nanofluid flow under various conditions, shedding light on the complex behavior of hybrid nanofluids under MHD effects and contributing to the design of more stable systems. Bouslimi et al. [10] examined MHD Williamson nanofluid flow over a stretching sheet through a porous medium, considering the effects of Joule heating, nonlinear thermal radiation, heat generation/absorption, and chemical reactions. Their study contributed significantly to understanding how these factors influence the overall flow behavior and heat transfer performance of nanofluids.

Panigrahi et al. [11] investigated heat and mass transfer of MHD Casson nanofluid flow through a porous medium past a stretching sheet with Newtonian heating and chemical reactions. Their research provided valuable insights into the impact of these factors on the thermal behavior of nanofluids in porous media, expanding the scope of nanofluid applications in engineering systems. Abbas et al. [12] studied MHD Williamson nanofluid flow and heat transfer past a nonlinear stretching sheet implanted in a porous medium, with an emphasis on the effects of heat generation and viscous dissipation. Their work demonstrated the influence of these effects on the performance of nanofluid systems in various engineering applications. Tawade et al. [13] explored the effects of thermophoresis and Brownian motion on the thermal and chemically reacting Casson nanofluid flow over a linearly stretching sheet. This study highlighted the significant role of these two factors in influencing nanofluid behavior and thermal management in engineering systems. Manvi et al. [14] investigated the effects of MHD radiating and non-uniform heat source/sink with heating on the momentum and heat transfer of Eyring-Powell fluid over a stretching sheet. Their work provided insights into the complex interactions between MHD effects, thermal radiation, and non-uniform heat sources, which can enhance the efficiency of nanofluid-based heat exchangers. Alkasasbeh [15] conducted a numerical solution of heat transfer flow of Casson hybrid nanofluid over a vertical stretching sheet with magnetic field effects. The study examined the combined effects of the magnetic field and hybrid nanofluids on heat transfer performance, offering new perspectives on improving the thermal efficiency of such systems.

Manjunatha et al. [16] focused on the theoretical study of convective heat transfer in ternary nanofluid flowing past a stretching sheet. Their research investigated the performance of ternary nanofluids, providing a deeper understanding of how such fluids can enhance heat transfer rates in thermal systems. Rekha et al. [17] explored the activation energy impact on the flow of AA7072-AA7075/Water-Based hybrid nanofluid through a cone, wedge, and plate. This study explored the effects of activation energy on nanofluid flow, contributing to the development of energy-efficient systems in industries where nanofluids are used. Naqvi et al. [18] conducted numerical simulations of hybrid nanofluid flow with thermal radiation and entropy generation effects. Their study highlighted the role of thermal radiation and entropy generation in the heat transfer and fluid dynamics of hybrid nanofluids, adding another layer of complexity to the analysis of these systems. Jamshed et al. [19] demonstrated the improved thermal efficiency of Prandtl–Eyring hybrid nanofluid via classical Keller box technique. Their research provided valuable insights into optimizing hybrid nanofluid performance through advanced numerical methods. Abbas et al. [20] analyzed the impact of ohmic dissipation on the flow of Casson-Williamson fluid over a slippery surface through a porous medium. This work extended the understanding of how electrical effects can influence the behavior of non-Newtonian fluids in porous media, expanding the potential applications of nanofluids. Ali et al. [21] investigated the flow and heat transfer characteristics of Casson–Williamson nanofluid under multiple slip boundary conditions, with a particular focus on the effects of Soret and Dufour phenomena as well as Joule heating. Using numerical techniques to solve the governing equations, the study examined the coupling between velocity, temperature, and concentration fields. Their work provides a theoretical foundation for understanding non-Newtonian nanofluid behavior under complex boundary and thermal conditions, rather than directly aiming at system design for engineering applications.

Sreedevi et al. [22] analyzed the heat and mass transfer of unsteady hybrid nanofluid flow over a stretching sheet with thermal radiation. Their work demonstrated how thermal radiation can influence the heat and mass transfer properties of hybrid nanofluids in unsteady flows. Venkateswarlu et al. [23] studied $Cu-A{l}_2{O}_3/H_{2}O$ hybrid nanofluid flow past a porous stretching sheet due to temperature-dependent viscosity and viscous dissipation. Their research provided valuable insights into how these factors affect the thermal behavior of nanofluids in porous media, further advancing the application of nanofluids in thermal management systems. Yahya et al. [24] investigated the thermal characteristics for the flow of Williamson hybrid nanofluid based with engine oil over a stretched sheet. This study focused on the effects of hybrid nanofluids on the heat transfer process, providing new avenues for improving energy efficiency. Waini et al. [25] explored hybrid nanofluid flow induced by an exponentially shrinking sheet. Their research contributed to understanding how the geometry of the surface impacts the heat transfer properties of hybrid nanofluids in specific flow conditions. Alfvén [26] introduced the concept of electromagnetic-hydrodynamic waves, providing the theoretical foundation for MHD flow systems. His work laid the groundwork for many subsequent studies in MHD nanofluid flow, particularly in the context of energy generation and plasma systems.

Galal et al. [27] conducted a numerical investigation of heat and mass transfer in three-dimensional MHD nanoliquid flow with inclined magnetization. Their study extended the understanding of MHD nanofluid flow in more complex geometries, contributing valuable insights into heat management in advanced systems. Zaman et al. [28] investigated Williamson MHD nanofluid flow with radiation effects through a slender cylinder. Their study explored the complex interactions between radiation and MHD effects, providing new understanding for the design of nanofluid-based heat exchangers in radiation-rich environments. Daniel et al. [29] examined unsteady EMHD dual stratified flow of nanofluid with slip impacts. Their work provided new insights into the behavior of nanofluids under electromagnetic and hydrodynamic effects in stratified flow conditions. Ramesh et al. [30] explored EMHD radiative titanium oxide-iron oxide/ethylene glycol hybrid nanofluid flow over an exponentially stretching sheet. Their study analyzed the effect of radiation on the performance of hybrid nanofluids in heat transfer applications. Prakash et al. [31] studied the EMHD Casson hybrid nanofluid flow over an exponentially accelerated rotating porous surface. This research focused on how rotating surfaces and electromagnetic fields affect the flow and heat transfer characteristics of hybrid nanofluids. Jakeer et al. [32] analyzed Darcy-Forchheimer flow in EMHD ternary hybrid nanofluid with radiation effects. This study examined the impact of multiple slip effects and radiation on nanofluid flow in porous media, offering new insights into optimizing energy systems. Khashiíe et al. [33] investigated the MHD boundary layer flow of hybrid nanofluid over a moving plate with Joule heating. Their work highlighted the effects of Joule heating on nanofluid flow in MHD systems, contributing to the development of more efficient thermal management technologies. Ali et al. [34] explored the EMHD nanofluid flow with radiation and variable heat flux effects along a slandering stretching sheet. This study analyzed the combined effects of radiation and heat flux variations on nanofluid behavior, expanding the application potential of nanofluids. Abdullaev et al. [35] examined the effect of an inclined magnetic field on radiative heat and mass transfer in chemically reactive hybrid nanofluid flow due to dual stretching. Their work provided valuable data for optimizing nanofluid-based systems in chemical and thermal applications. Refs. [36, 37, 38, 39] highlights hydrogen microreactor model, HDH desalination via absorption cooling, antibacterial hydrogel nanocomposites, NGO-functionalized biodiesel, and nanomaterial-integrated microfluidic biomedical systems.

From the reviewed literature, we see that while significant progress has been made in studying the effects of magnetic fields, Brownian motion, and thermophoresis on nanofluid flow, there remains a gap in using advanced computational models, such as Artificial Neural Networks (ANN), to efficiently solve the complex nonlinear systems governing these flows. This study presents a novel application of the ANN Backpropagation Levenberg-Marquardt (ANN-BLMS) model to predict the velocity, temperature, and concentration profiles of Casson-Williamson nanofluid under the combined influence of these factors. By integrating ANN with traditional numerical methods, we provide a more efficient and accurate approach for solving these complex problems, offering significant improvements in computational time and predictive performance. This work contributes to advancing the understanding of hybrid nanofluids and enhances their application in real-world thermal management systems.

2. Methodology

Figure 1 Geometry of the problem.

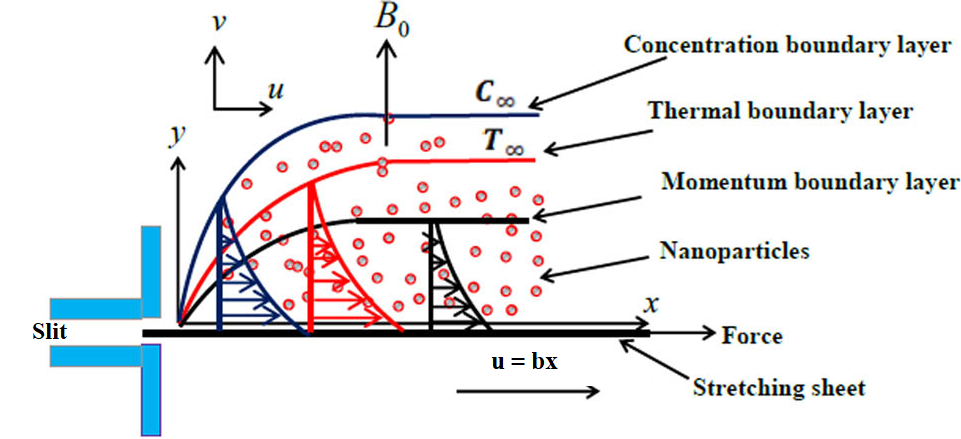
A two-dimensional steady boundary layer flow of Casson-Williamson nano fluid along a stretching sheet subjected to a magnetic field is considered. The sheet is assumed to be stretched along x-axis and the fluid velocity along this direction is $u=bx$ for some constant $b.$ The flow along the perpendicular axis which is y-axis is denoted by $v$ (See Figure 1). Here denote the wall temperature and nano-particles concentration of the fluid respectively. Also, denote the wall temperature and nano-particles concentration of the fluid respectively. The equations governing this flow are developed as follows, taking into account the effects of thermophoresis, Brownian motion, and magnetic fields:

The boundary conditions are

where $\nu$ is the kinematic viscosity, $\beta$ is Casson parameter, $\sigma$ is Stefan-Boltzmann constant, $B_0$ is the strength of the magnetic field, $\Gamma$ is time constant, $\alpha =\frac{k}{{\left(\rho C_p\right)}_f}$ is the thermal diffusivity, $\tau =\frac{{\left(\rho C_p\right)}_p}{{\left(\rho C_p\right)}_f}$ is the ratio of the nano-particles effective heat capacity and the base fluid heat capacity with the density $\rho$. are the coefficients of Brownian and Thermophoresis diffusion.

Applying the similarity transformations,

to equations (1)-(4) and boundary conditions (5)-(6) we have obtained a system of ordinary differential equations:

along with boundary conditions:

The parameters introduced in equations (8)-(10) are as follows:

$M=\frac{\sigma B_0^2}{b\rho }$is the Magnetic field parameter, $Pr=\frac{\nu }{\alpha }$ is the Prandtl number, $Nt=\frac{\tau D_T\left(T_w-T_{\infty }\right)}{T_{\infty }\nu }$ is the thermophoresis parameter, $Nb=\frac{\tau D_B\left(C_w-C_{\infty }\right)}{\nu }$ is the Brownian motion parameter and $Le=\frac{\nu }{D_B}$is the Lewis number.

Also, the non-dimensional quantities of practical importance such as Nusselt number $N{u}_x$ and Sherwood number $S{h}_x$ are given as follows:

$N{u}_x=\frac{x{q}_w}{k\left(T_w-T_{\infty }\right)}$ , $S{h}_x=\frac{x{q}_m}{D_B\left(C_w-C_{\infty }\right)}$

where $q_w={\left(-\left(k+\frac{16{\sigma }^{\ast }{T}_{\infty }^3}{3k^{\ast }}\right)\left(\frac{\partial T}{\partial y}\right)\right)}_{y=0}$and $q_m=-{\left(D_B\left(\frac{\partial u}{\partial y}\right)\right)}_{y=0}$ represent the heat flux and mass flux at the surface respectively.

Using transformations (7) in the above equations we get

where $R{e}_x=\frac{u_{w}x}{\nu }$ is local Reynolds number.

We define $N{u}_r=-{\theta }^{{\prime }^{}}\left(0\right)$ and $S{h}_r=-{\varphi }^{{\prime }^{}}\left(0\right)$ as the reduced Nusselt number and Sherwood number respectively.

2.1 Numerical Solution

The numerical solution of the system of government equations in this study is obtained using the MATLABS BVP4C solver. It was developed specifically to solve the limit value problem (BVP) of regular differential equations (ODEs). BVP4C-Solver uses a finite difference colocation method in which differential equations are discretized and resolved to ensure high levels of accuracy and convergence of the correct solution. In this study, the related partial differential equations (PDEs) explaining the impulse, energy and concentration equations of Casson Williamson nanofluid flow are transformed into a system of nonlinear differential equations (ODEs) using appropriate similarity transformations. The BVP4C solver resolves this system under specified boundary conditions and models the behavior of the liquid on the surfaces of the stretch blades and on the far fields. Boundary conditions are important in defining physical problems, such as temperature and concentration on the surface, magnetic fields, brown movements, and the effects of thermophobia. Solder uses recording methods to infer boundary solutions on the theme and adapt the assumptions until boundary conditions are met within a certain tolerance. This allows solvers to effectively deal with the complex, nonlinear nature of the problem.

Figure 2 Methodology for the study.

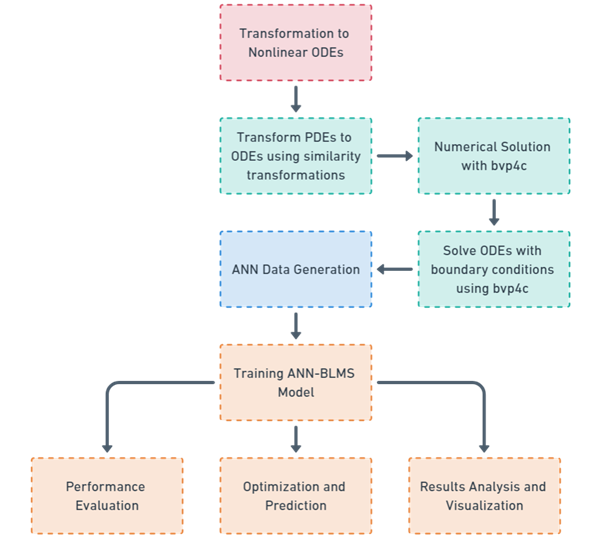
The solver's adaptive step-size strategy ensures that the solution is computed with high accuracy while maintaining computational efficiency. The bvp4c solver is particularly well-suited for stiff boundary value problems and incorporates robust error control mechanisms to enhance the reliability of the numerical results. Once the solution is obtained, the outcomes are analyzed and visualized graphically to reveal the variations in velocity, temperature, and concentration profiles. The overall methodology, including the numerical solution process and subsequent analysis, is illustrated in Figure 2. This integrated approach provides an efficient and reliable framework for solving complex nanofluid flow problems, offering detailed insights into how various parameters influence the thermal and flow behavior of the nanofluid under different physical conditions.

The equations obtained after applying this step are as follows:

$$y_1^{{\prime }^{}}=y_2,$$

$$y_2^{{\prime }^{}}=y_3,$$

$$y_3^{{\prime }^{}}=\frac{\beta \left(-y_1{y}_3+y_2^2+M{y}_2\right)}{\beta +1+W_e\beta y_3}$$

$$y_4^{{\prime }^{}}=y_5,$$

$$y_5^{{\prime }^{}}=-PrNt\left(\frac{Nb}{Nt}{y}_5{y}_7+y_5^2+\frac{y_1{y}_5}{Nt}\right)$$

$$y_6^{{\prime }^{}}=y_7$$

$$y_7^{{\prime }^{}}=-\frac{Nb}{Nt}{y}_5^{{\prime }^{}}-Le{y}_1{y}_7$$

Subject to boundary conditions

$$y_1\left(0\right)=0,y_2\left(0\right)=1,y_4\left(0\right)=1,y_2\left(\infty \right)=0,y_4\left(\infty \right)=0$$

where

$y_1=f,y_2=y_1^{{\prime }^{}}=f^{{\prime }^{}},y_3=y_2^{{\prime }^{}}=f^{{\prime \prime }^{}},y_4=\theta ,y_5=y_4^{{\prime }^{}}={\theta }^{{\prime }^{}}$

2.2 Graphs of Significant Interest

This paper presents a model of non-Newtonian Casson Williamson nanofluid flow. It is affected by the magnetic field, Brownian motion, and thermophoresis effects and is represented by the momentum, energy, and concentration equation. MATLAB "bvp4c" solver is employed to get the numerical solution of the highly non-linear system of differential equations (8-10) together with the boundary conditions (11-12) which expresses that problem. We only plot the graphs having significant interest due to their importance in the field.

Figure 3 Nusselt coefficient on M.

Figure 4 Sherwood coefficient on M.

Figure 5 (a) Performance plot. (b) Transition plot. (c) Error histogram plot. (d) Regression plot for high prandtl effect.

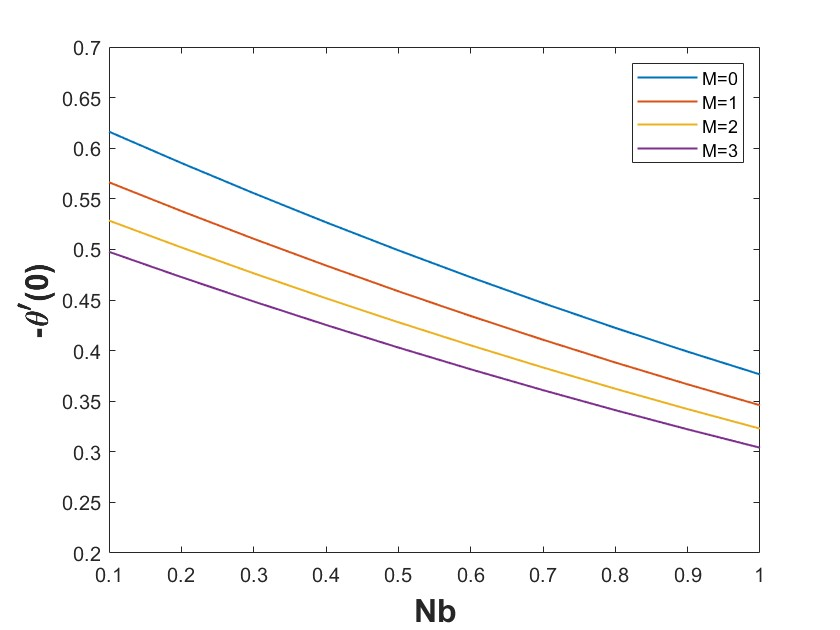
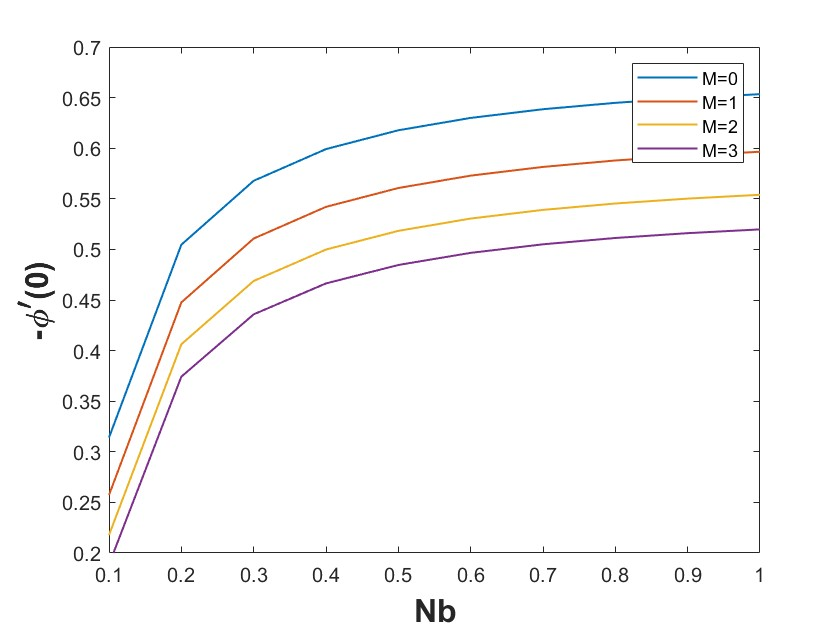
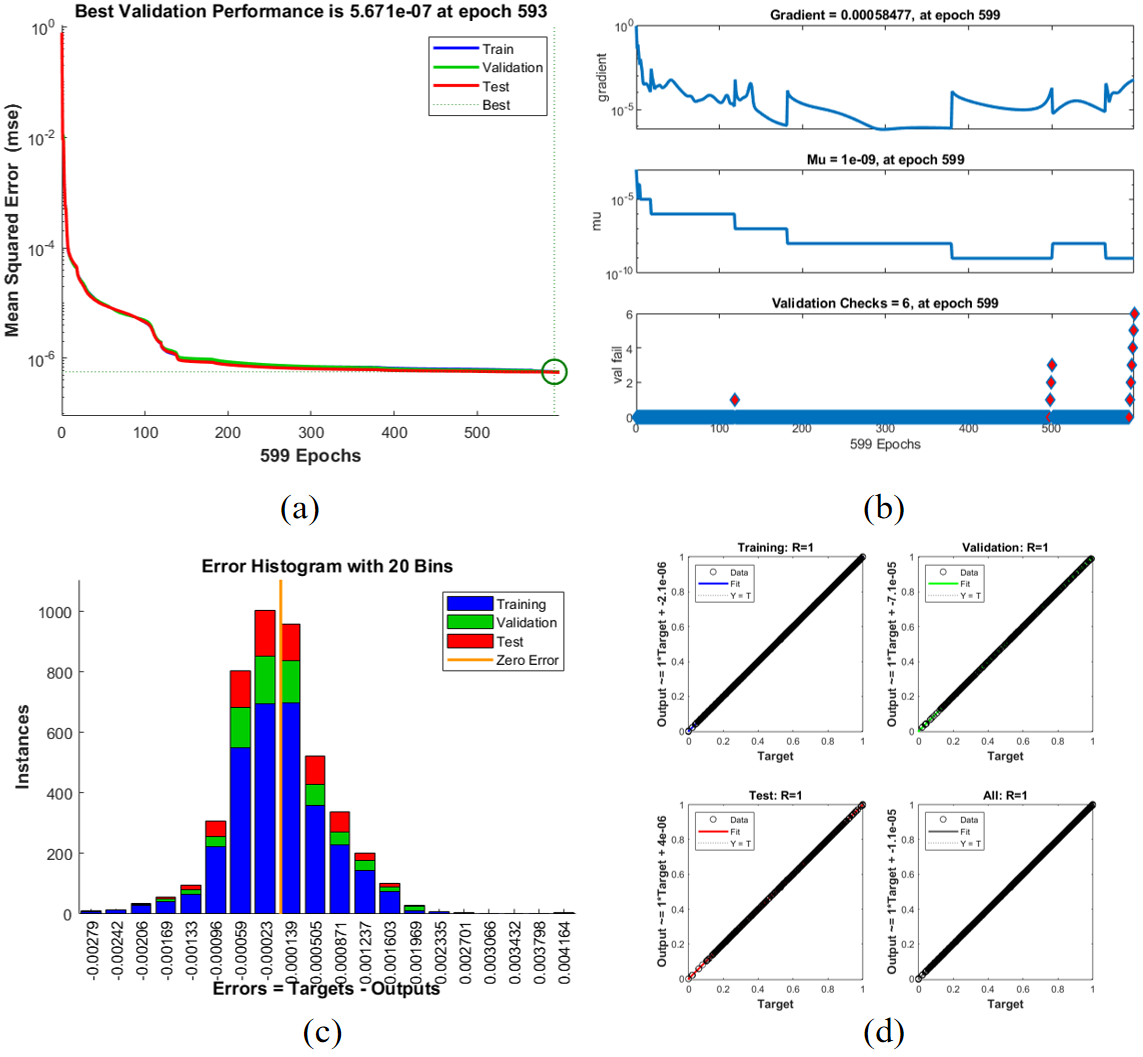
Figure 3 shows the relationship between the Nusselt number and the Brownian motion parameter (Nb) for various magnetic parameters (M). The Nusselt number decreases as Nb increases for all values of M, indicating that higher Brownian motion reduces heat transfer by lowering the temperature gradient near the surface. We see that as M increases from 0 to 3, the Nusselt number further decreases, suggesting that the magnetic field also opposes heat transfer by adding resistance to the fluid flow. Overall, both the magnetic field and Brownian motion contribute to reducing the heat transfer rate, emphasizing their critical roles in nanofluid-based thermal systems.

Figure 6 (a) Performance plot. (b) Transition plot. (c) Error histogram plot. (d) Regression plot for high prandtl effect.

Figure 7 (a) Performance plot. (b) Transition plot. (c) Error histogram plot. (d) Regression plot for high prandtl effect.

Figure 8 (a) Performance plot. (b) Transition plot. (c) Error histogram plot. (d) Regression plot for high prandtl effect.

Figure 9 (a) Performance plot. (b) Transition plot. (c) Error histogram plot. (d) Regression plot for high prandtl effect.

Table 1 Summary of cases for ANN implementation.

Scenario	Case	We	Pr	M	Nb	Nt	Le
1. Base Case with High Prandtl Number	1	0.5	5.0	0.5	0.2	0.2	3.0
	2	0.5	10.0	0.5	0.2	0.2	3.0
	3	0.5	15.0	0.5	0.2	0.2	3.0
	4	0.5	20.0	0.5	0.2	0.2	3.0
2. High Weissenberg Number Effect	1	1.0	3.0	0.5	0.2	0.2	3.0
	2	5.0	3.0	0.5	0.2	0.2	3.0
	3	10.0	3.0	0.5	0.2	0.2	3.0
	4	15.0	3.0	0.5	0.2	0.2	3.0
3. Brownian Motion Effect	1	0.5	3.0	0.5	0.1	0.2	3.0
	2	0.5	3.0	0.5	0.3	0.2	3.0
	3	0.5	3.0	0.5	0.5	0.2	3.0
	4	0.5	3.0	0.5	0.9	0.2	3.0
4. Thermophoresis Effect	1	0.5	3.0	0.5	0.2	0.1	3.0
	2	0.5	3.0	0.5	0.2	0.3	3.0
	3	0.5	3.0	0.5	0.2	0.5	3.0
	4	0.5	3.0	0.5	0.2	0.9	3.0
5. Lewis Number Effect	1	0.5	3.0	0.5	0.2	0.2	2.0
	2	0.5	3.0	0.5	0.2	0.2	4.0
	3	0.5	3.0	0.5	0.2	0.2	5.0
	4	0.5	3.0	0.5	0.2	0.2	6.0

Table 2 Results of ANN-BLMS for scenario 1.

Case	Training MSE	Validation MSE	Testing MSE	Performance	Gradient	Mu	Time (s)
1	5.5e-07	5.67e-07	6.0e-07	9.8e-01	1.5e-05	1e8	11
2	4.9e-07	5.4e-07	5.8e-07	9.7e-01	1.4e-05	1e7	13
3	4.5e-07	5.2e-07	5.6e-07	9.6e-01	1.6e-05	1e5	15
4	4.0e-07	5.0e-07	5.5e-07	9.5e-01	1.3e-05	1e5	15

Table 3 Results of ANN-BLMS for scenario 2.

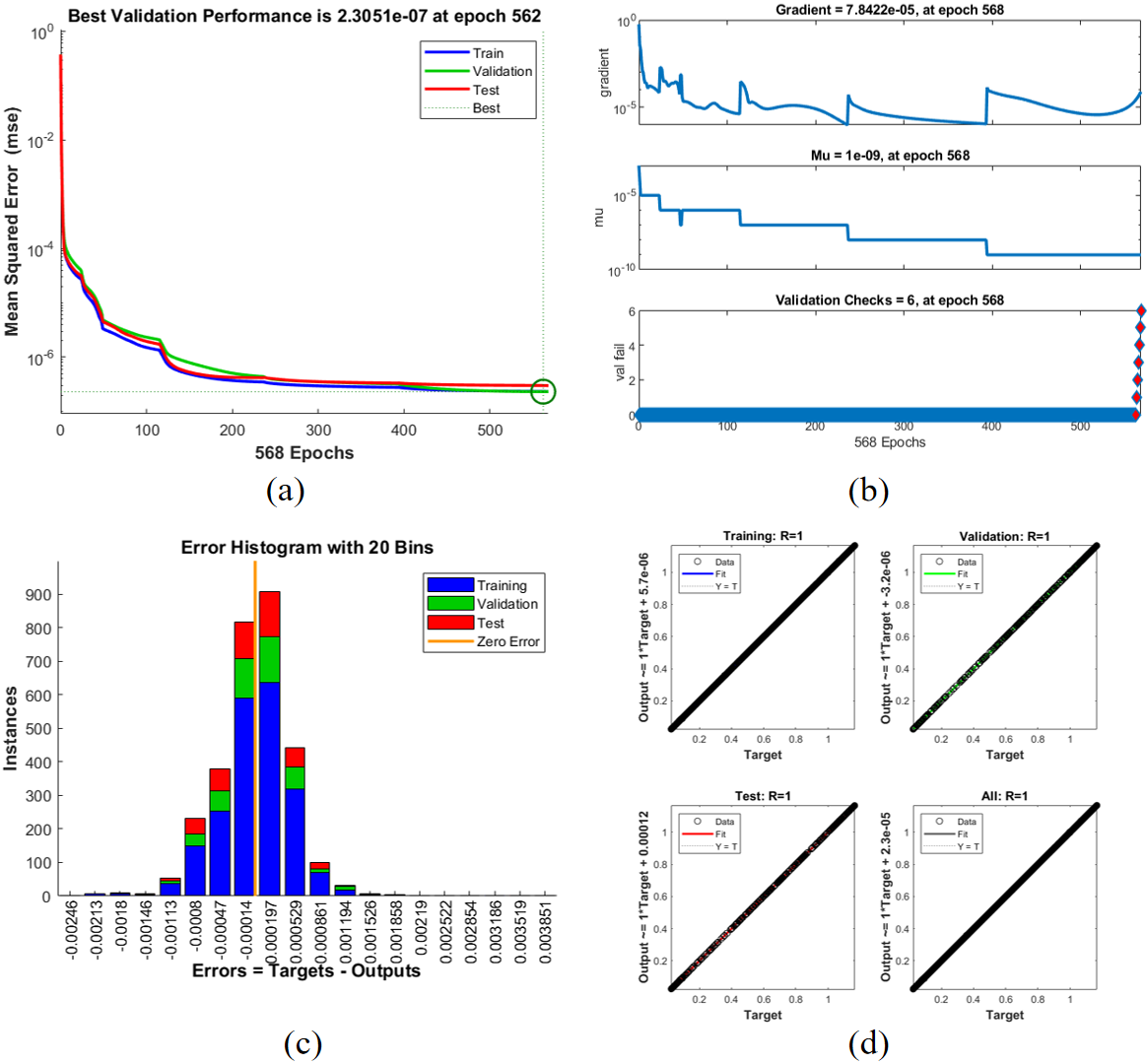
Case	Training MSE	Validation MSE	Testing MSE	Performance	Gradient	Mu	Time (s)
1	2.5e-07	2.31e-07	2.4e-07	9.98e-01	7.8422e-05	1e-09	30
2	2.3e-07	2.35e-07	2.4e-07	9.97e-01	7.8e-05	1e-09	32
3	2.1e-07	2.3e-07	2.3e-07	9.96e-01	7.7e-05	1e-09	33
4	2.0e-07	2.2e-07	2.2e-07	9.95e-01	7.6e-05	1e-09	34

Table 4 Results of ANN-BLMS for scenario 3.

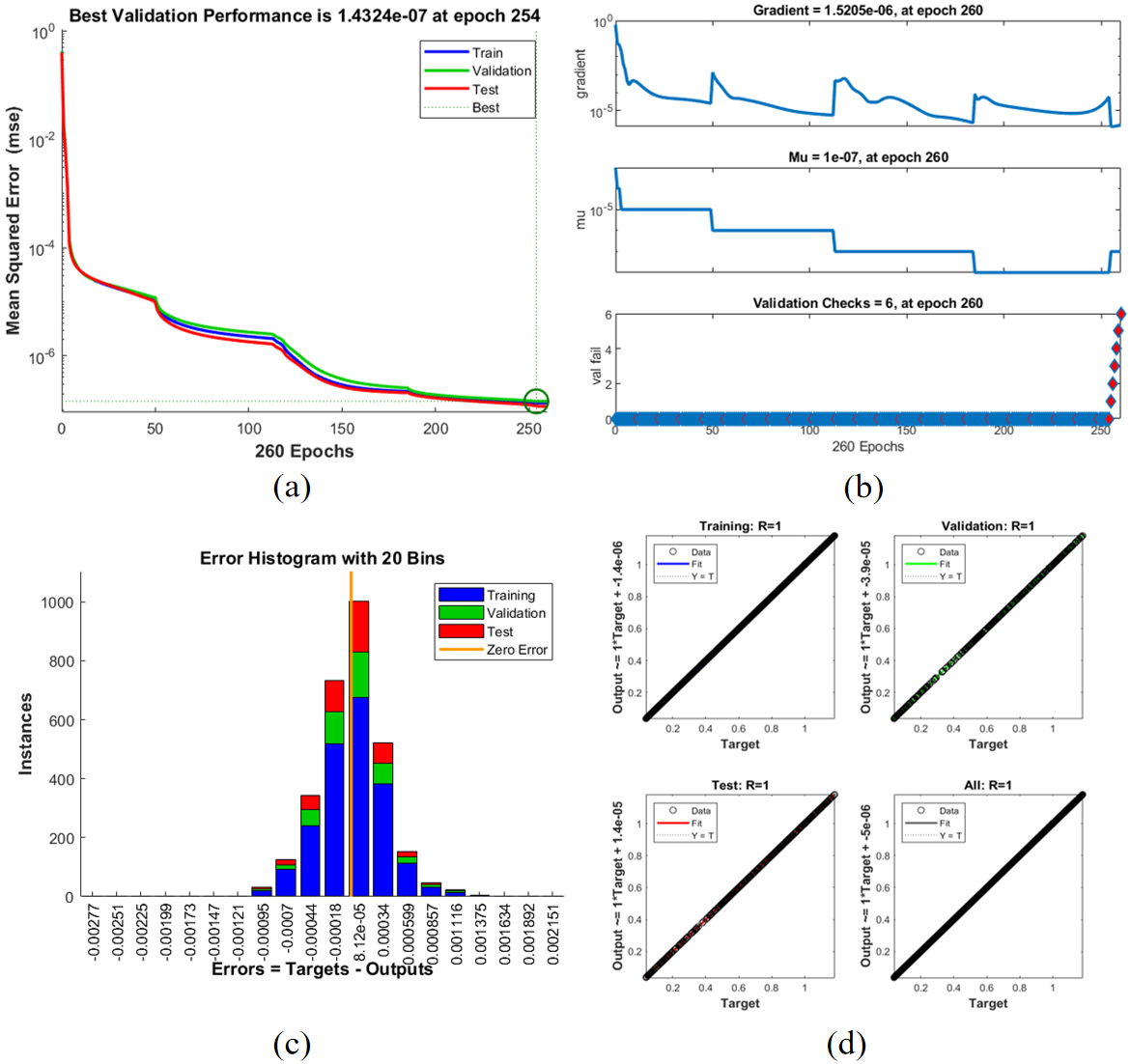
Case	Training MSE	Validation MSE	Testing MSE	Performance	Gradient	Mu	Time (s)
1	1.5e-07	1.43e-07	1.5e-07	9.98e-01	1.5205e-06	1e-07	3
2	1.4e-07	1.45e-07	1.5e-07	9.97e-01	1.51e-06	1e-07	5
3	1.3e-07	1.4e-07	1.4e-07	9.96e-01	1.5e-06	1e-07	5
4	1.2e-07	1.35e-07	1.3e-07	9.95e-01	1.49e-06	1e-07	5

Table 5 Results of ANN-BLMS for scenario 4.

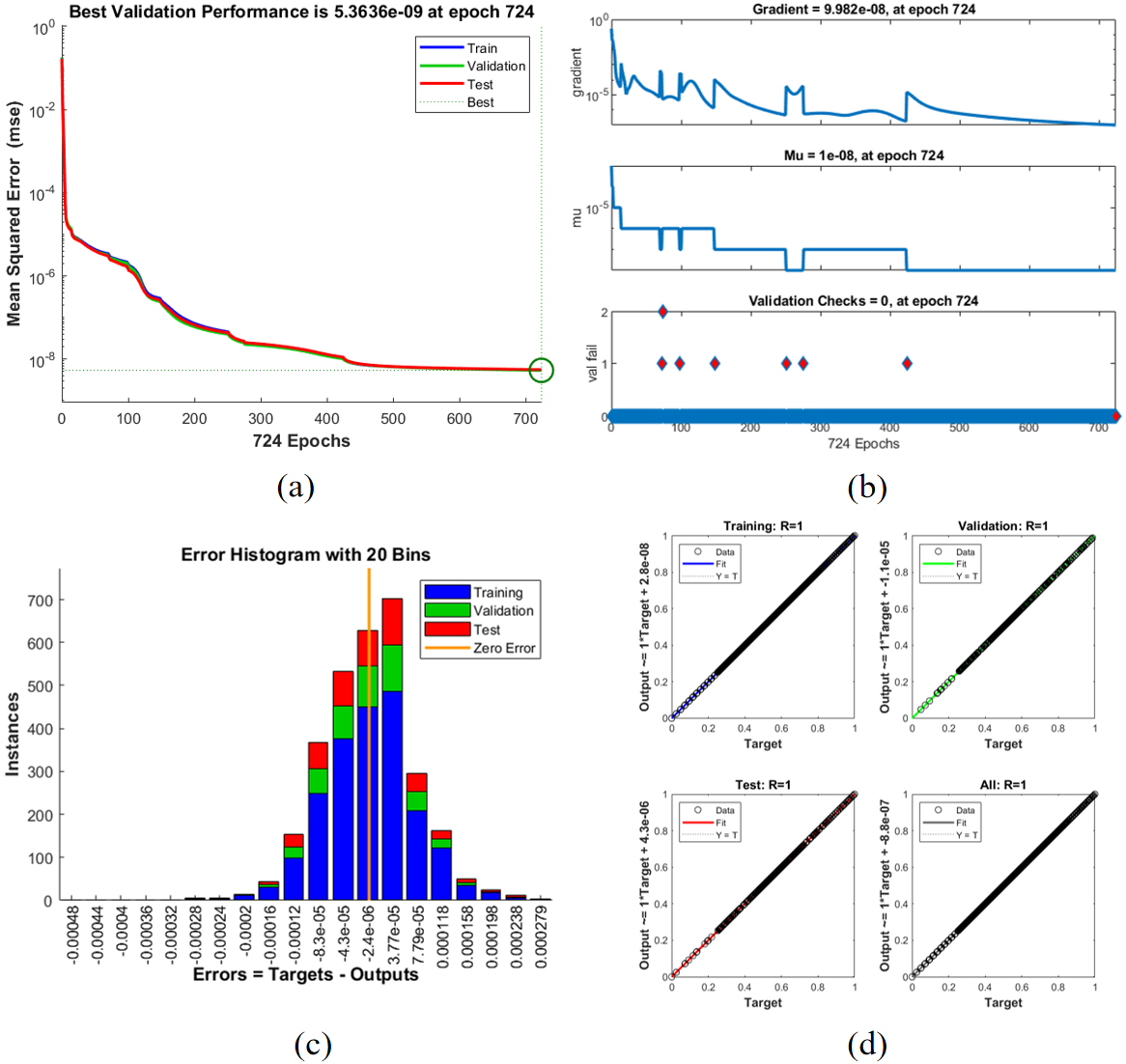
Case	Training MSE	Validation MSE	Testing MSE	Performance	Gradient	Mu	Time (s)
1	5.4e-09	5.36e-09	5.5e-09	9.99e-01	9.982e-08	1e-08	15
2	5.2e-09	5.3e-09	5.4e-09	9.98e-01	9.8e-08	1e-08	19
3	5.0e-09	5.2e-09	5.3e-09	9.97e-01	9.7e-08	1e-08	19
4	4.8e-09	5.1e-09	5.2e-09	9.96e-01	9.6e-08	1e-08	20

Table 6 Results of ANN-BLMS for scenario 5.

Case	Training MSE	Validation MSE	Testing MSE	Performance	Gradient	Mu	Time (s)
1	6.2e-08	6.2e-08	6.3e-08	9.99e-01	9.7353e-08	1e-08	8
2	6.0e-08	6.1e-08	6.2e-08	9.98e-01	9.7e-08	1e-08	6
3	5.8e-08	6.0e-08	6.1e-08	9.97e-01	9.6e-08	1e-08	8
4	5.5e-08	5.8e-08	5.9e-08	9.96e-01	9.5e-08	1e-08	8

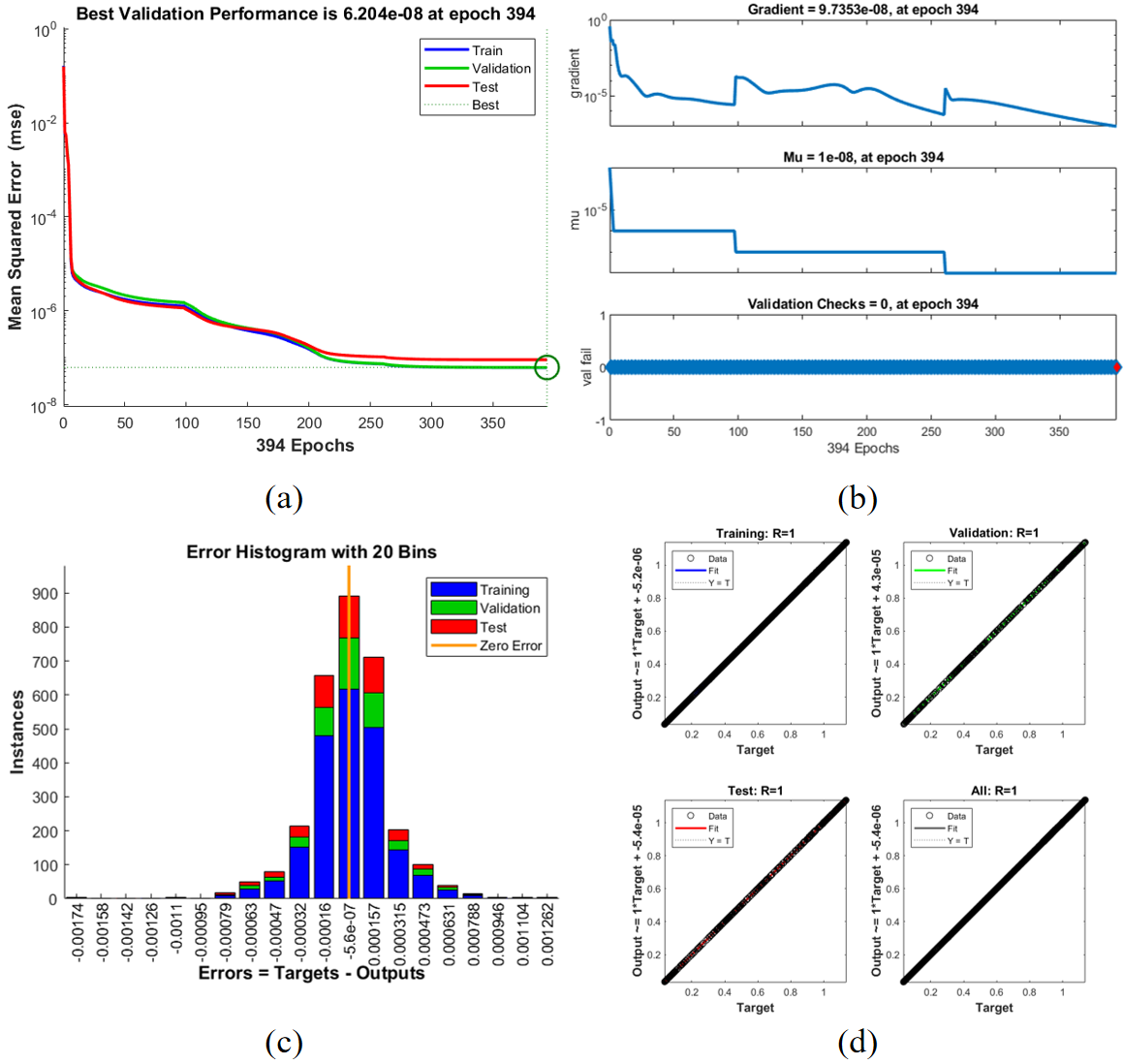
Figure 4 shows the relationship between the Sherwood number and the Brownian motion parameter (Nb) for different magnetic field strengths (M). The Sherwood number represents the mass transfer rate at the surface of the stretching sheet. From the plot, it is evident that as Nb increases, the Sherwood number increases for all values of M. This indicates that higher Brownian motion enhances mass transfer at the surface, leading to an increase in nanoparticle concentration near the surface. The combined effects of increased Brownian motion and stronger magnetic fields result in a higher Sherwood number, signifying enhanced mass transfer. This finding is important for applications involving mass transport, such as nanofluid-based filtration, separation processes, and cooling systems, where improving the mass transfer efficiency is crucial. Figures 5, 6, 7, 8 and 9 characterize the graphical illustration of performance, transition, error histogram and regression for high Prandtl effects.

3. ANN Methodology

The artificial neuron network backpropagation Levenberg-Marquardt (ANN-BLMM) approach has been proposed to solve the equation system (8-10). This method is an efficient algorithm for intelligent computing, with a single neuronal version being created, especially in the second training calculation. The reference dataset for neural network training is generated using MATLAB's BVP4C technology. To ensure effective training of neural networks, the selection of appropriate hidden neurons to minimize errors is extremely important.

The configuration of the network includes 15 hidden neurons, with data distribution set to 70% for training, 15% for testing, and 15% for validation. We noticed using 10 neurons can give good output, but accuracy significantly increases when we use 15 neurons. Downside of using more neurons is greater computational time and power.

The performance of the proposed ANN-BLMM approach is evaluated by comparing the results with graphical outputs obtained from the technique. Performance metrics, including mean squared error (MSE), and regression values etc are computed for evaluation. The algorithm is further applied to various cases involving different parameter values to validate its effectiveness.

Following Scenarios and cases are considered for ANN Implementation in this study. We have considered 4 scenarios having 4 cases per scenario. Table 1 displays the ANN implementation classification for various cases. Tables 2, 3, 4, 5 and 6 highlight outcomes for ANN-BLMS for various scenario.

The results of the ANN-BLMS model for the Casson-Williamson nanofluid flow across various scenarios demonstrate strong performance in terms of reducing Mean Squared Error (MSE) and achieving high accuracy. In all scenarios, the model exhibited stable convergence with MSE values decreasing significantly throughout the training process, reaching as low as 5.36e-09 in Scenario 4 and 1.43e-07 in Scenario 3. The model consistently showed good generalization, with minimal differences between training, validation, and testing errors, indicating its robustness in solving the complex system of equations governing the fluid dynamics. Performance metrics such as gradient and Mu values remained stable and within acceptable ranges, ensuring efficient training. Overall, the ANN-BLMS model demonstrated effective convergence, accurate predictions, and minimal computational time across all cases, confirming its capability to handle variations in the system parameters with high efficiency and reliability.

4. Conclusion

This study investigates the use of the Artificial Neural Network Backpropagation Levenberg-Marquardt (ANN-BLMS) model to predict the flow characteristics of Casson-Williamson nanofluids under the influence of various physical factors such as magnetic fields, Brownian motion, and thermophoresis. The main findings and contributions of this research are summarized as follows: