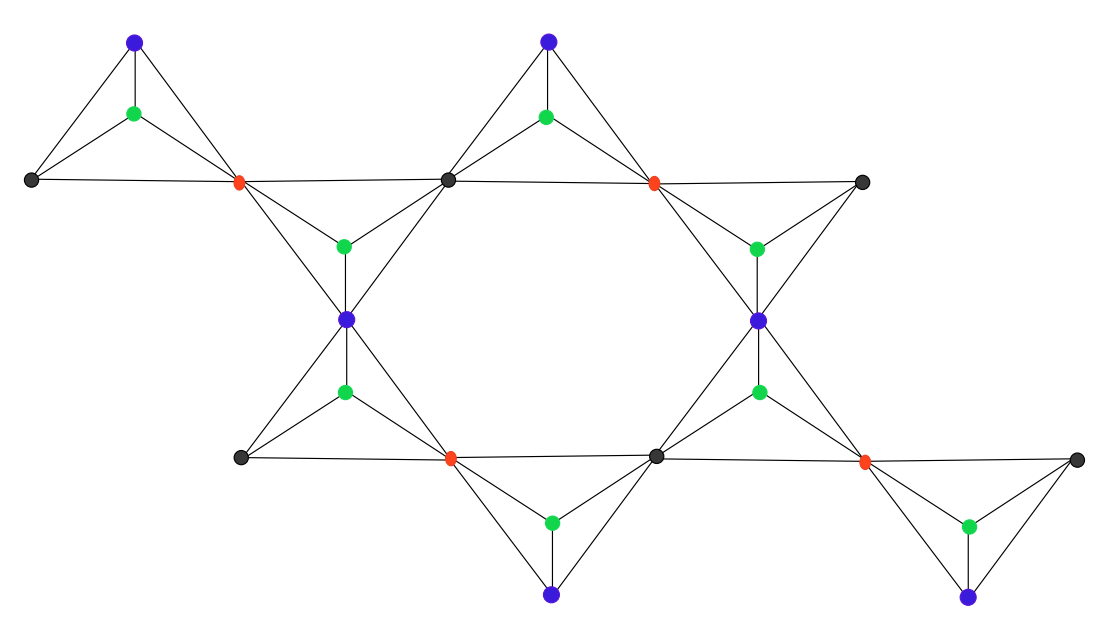
In this article, we specially focused on rhombus silicate molecular structure. Graph is a data structure for describing complex systems, which contains a set of objects and relationships. A molecular graph, also known as a chemical graph, is a graph-theoretic representation of the structural formula of a chemical compound used in chemical graph theory and mathematical chemistry. A chemical graph is a labelled graph whose edges represent covalent bonds and vertices represent the atoms. A set of vertices (atoms) of a graph G is known as its dominating set with respect to the vertices, if every vertex other than that set is adjacent to some vertex in set. The vertex and edge dominating sets, to... More >

Three-dimensional (3D) flow of a viscoelastic fluid in the neighborhood of new family of modified stagnation point depending on shear to strain ratio over a flat surface is numerically investigated. Similarity equations are obtained from the fundamental conservation laws of mass, momentum, energy and nanoparticle concentration. The resulting set of nonlinear equations are solved numerically using an implicit finite difference scheme known as Keller-Box Method. A comparative analysis for modified Hiemenz flow, non-axisymmetric stagnation point and axisymmetric stagnation point flow is carried out. Velocity, temperature and concentration profiles, skin frictions local Nusselt and Sherwood numb... More >

In the current study, a new approach had been constructed to define new maps using the concept of bornological semi open and bornological semi closed sets, which includes sequential bornological semi continuous maps, bornological semi closed (open) maps, bornological strongly semi closed (open) maps, and bornological semi-irresolute closed (open) maps. We investigate and study the properties of these concepts. More >

This paper investigates the bio-convective behavior of a third-grade non-Newtonian nanofluid over a stretching sheet. While the influence of Newtonian fluid flow based on classical Fourier and Fick’s laws has been widely discussed in previous studies, this work focuses on a novel third-grade nanofluid model incorporating various physical effects. Notably, the classical Fourier law is replaced by the Cattaneo–Christov (CC) theory for both heat and mass fluxes, capturing relaxation phenomena in the presence of bioconvective effects. Heat and mass transport are modeled using the CC framework, and nanoscale mechanisms are described via the Buongiorno nanofluid model. The influences of thermo... More >

This study presents a mathematical framework to analyze the transmission dynamics of the Ebola Virus Disease (EVD) using an extended SEIRVH model. The model incorporates vaccinated and hospitalized compartments, addressing critical factors such as vaccination efficacy, healthcare interventions, and natural disease progression. Differential equations describe the transitions between six population compartments. The study evaluates model stability and bifurcation through well-posedness, positivity, and boundedness analyzes, ensuring realistic and biologically valid solutions. The basic reproduction number, R0, derived from the next generation matrix, serves as a threshold for outbreak control.... More >