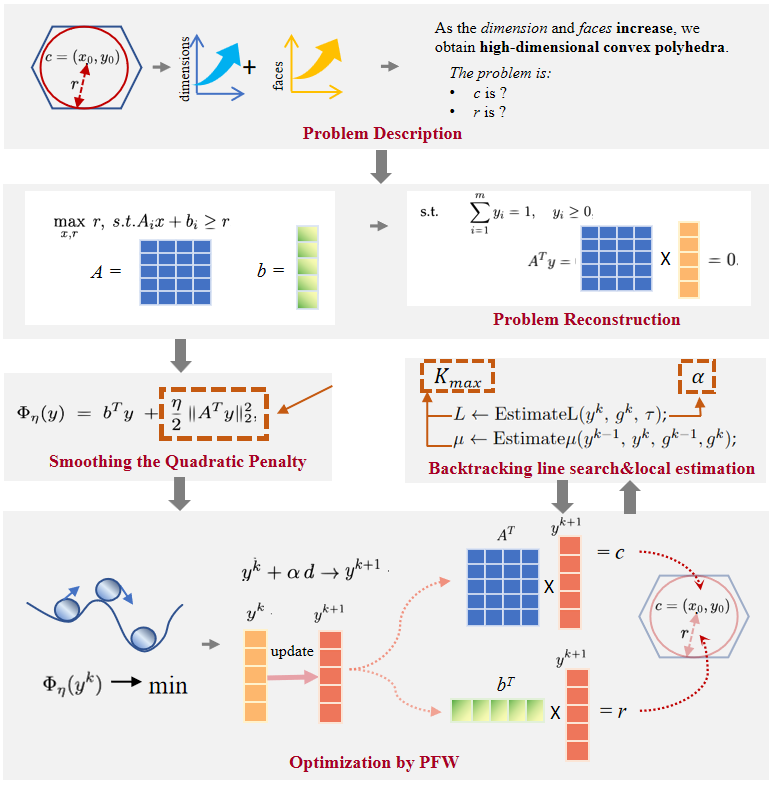
As a classical convex optimization problem in geometry, computing the maximum inscribed ball (MaxIB) in ultra-high-dimensional polytopes is critical for enabling real-time IoT applications, such as optimal deployment of sensor networks, where polytopes model physical constraints arising from obstacles or coverage boundaries. However, existing methods suffer from the curse of dimensionality, leading to prohibitive computational costs. This paper develops a more efficient approach for computing the (1-\(\epsilon\))-approximate MaxIB in high-dimensional polytopes. To address these challenges, the problem is reformulated with adaptive penalty parameters to enforce strong convexity, enabling line... More >

Accurate predictions of traffic flow are very meaningful to city managers. With such information, traffic systems can better coordinate traffic signals and reduce congestion. By understanding traffic patterns, navigation systems can provide real-time routing suggestions that avoid traffic jams, save time, and reduce fuel consumption. However, traffic flow will be interfered with by multiple factors such as collection time and place. In this paper, stochastic configuration networks (SCNs) are proposed to predict the traffic flow. The network is trained through stepwise construction, and the network parameters are effectively optimized based on the approximation theorem and convergence analysi... More >