ICCK Transactions on Advanced Computing and Systems
ISSN: 3068-7969 (Online)
Email: [email protected]
Submit Manuscript
Edit a Special Issue
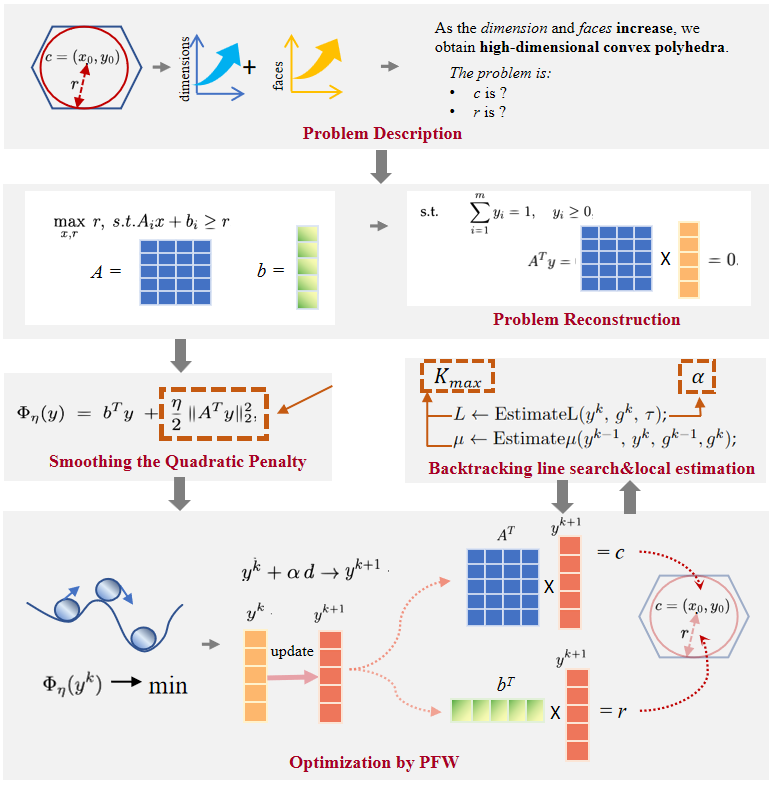
TY - JOUR AU - Lin, Yuqi PY - 2026 DA - 2026/01/14 TI - Pairwise Frank-Wolfe for Maximum Inscribed Balls: Enabling Real-Time Geometric Optimization JO - ICCK Transactions on Advanced Computing and Systems T2 - ICCK Transactions on Advanced Computing and Systems JF - ICCK Transactions on Advanced Computing and Systems VL - 2 IS - 1 SP - 61 EP - 73 DO - 10.62762/TACS.2025.318429 UR - https://www.icck.org/article/abs/TACS.2025.318429 KW - convex optimization KW - maximum inscribed ball KW - gradient optimization KW - Frank-Wolfe's Method AB - As a classical convex optimization problem in geometry, computing the maximum inscribed ball (MaxIB) in ultra-high-dimensional polytopes is critical for enabling real-time IoT applications, such as optimal deployment of sensor networks, where polytopes model physical constraints arising from obstacles or coverage boundaries. However, existing methods suffer from the curse of dimensionality, leading to prohibitive computational costs. This paper develops a more efficient approach for computing the (1-\(\epsilon\))-approximate MaxIB in high-dimensional polytopes. To address these challenges, the problem is reformulated with adaptive penalty parameters to enforce strong convexity, enabling linear convergence under the Pairwise Frank–Wolfe (PFW) algorithm. Furthermore, expensive exact line searches are replaced with a backtracking strategy, significantly reducing the per-iteration computational cost. Simulation results demonstrate more than a 12-fold acceleration over existing approximate MaxIB methods without sacrificing accuracy. SN - 3068-7969 PB - Institute of Central Computation and Knowledge LA - English ER -
@article{Lin2026Pairwise,
author = {Yuqi Lin},
title = {Pairwise Frank-Wolfe for Maximum Inscribed Balls: Enabling Real-Time Geometric Optimization},
journal = {ICCK Transactions on Advanced Computing and Systems},
year = {2026},
volume = {2},
number = {1},
pages = {61-73},
doi = {10.62762/TACS.2025.318429},
url = {https://www.icck.org/article/abs/TACS.2025.318429},
abstract = {As a classical convex optimization problem in geometry, computing the maximum inscribed ball (MaxIB) in ultra-high-dimensional polytopes is critical for enabling real-time IoT applications, such as optimal deployment of sensor networks, where polytopes model physical constraints arising from obstacles or coverage boundaries. However, existing methods suffer from the curse of dimensionality, leading to prohibitive computational costs. This paper develops a more efficient approach for computing the (1-\(\epsilon\))-approximate MaxIB in high-dimensional polytopes. To address these challenges, the problem is reformulated with adaptive penalty parameters to enforce strong convexity, enabling linear convergence under the Pairwise Frank–Wolfe (PFW) algorithm. Furthermore, expensive exact line searches are replaced with a backtracking strategy, significantly reducing the per-iteration computational cost. Simulation results demonstrate more than a 12-fold acceleration over existing approximate MaxIB methods without sacrificing accuracy.},
keywords = {convex optimization, maximum inscribed ball, gradient optimization, Frank-Wolfe's Method},
issn = {3068-7969},
publisher = {Institute of Central Computation and Knowledge}
}
Copyright © 2026 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. 
ICCK Transactions on Advanced Computing and Systems
ISSN: 3068-7969 (Online)
Email: [email protected]
Portico
All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/