ICCK Journal of Applied Mathematics
ISSN: 3068-5656 (Online)
Email: [email protected]


Fourier heat conduction model is the basic key for thermoelectric transport models [1]. However, a fundamental drawback of the widely used Fourier's law is that it describes a parabolic energy equation, which is valid for instantaneous propagation of thermal disturbances and consequently, the energy transport is anisotropic and assessment of unrealistics infinite heat propagation speed. To address this deficiency, a general structure known as Fourier's law with thermal relaxation was developed by Cattaneo [2] where a thermal relaxation time, representing the finite thermal conduction speed, was assigned. Exploiting this idea, Christov [3] goes a step further and improves the model by framing it in a frame-indifferent way using Oldroyd's theory of upper-convected derivatives, so that compatibility with the tenets of rational thermodynamics is achieved. The earlier work of Christov [3] initiated a series of studies of heat transfer with non-Fourier effects. Straughan [4] deduced the variation in thermal results subect to natural convective flow by improsing the non-tradtional Fourier's approach.
At the same time, there is a great interest in investigating different types of non-Newtonian fluids, ranging from everyday products to industrial liquids such as blood, ketchup, cheese, drilling mud, and colloidal suspensions. Of a variety of constitutive models, the 1944 Eyring–Powell fluid, originally proposed by Powell and Eyring, has been recognized for its ability to replicate Newtonian-like behavior at both low and high shear rates. Its empirical nature provides a more realistic description of complex rheological behavior, particularly for shear thickening and thinning phenomena. Several studies, including those by [5, 6, 7], have validated the versatility of the Eyring–Powell model in diverse flow configurations. [8] further advanced this field by incorporating ferromagnetic effects into the Eyring–Powell model while utilizing the Cattaneo-Christov (CC) heat flux theory. Their work highlights the necessity of coupling advanced heat conduction models with non-Newtonian flow theory to achieve accurate predictions of coupled heat and momentum transport. Recent progress in non-Newtonian fluid mechanics has expanded these insights: [9] investigated viscoelastic nanofluid transport under temperature gradients, while [10] analyzed Casson polymeric flows with radiative and non-Fourier effects. For bioconvective applications, [11] examined Eyring–Powell nanofluids over Riga surfaces, and [12] explored hybrid nanofluids with Hall current effects. Additionally, [13] developed numerical methods for fractional advection-diffusion systems, and [14, 15] addressed chemically reactive flows and double-diffusion phenomena in micropolar nanofluids.
Recent developments in fluid dynamics have emphasized the importance of varying sheet thickness on the behaviour of non-Newtonian fluids especially in industrial processes involving calendering and coating. Zahid et al. [16] studied the calendering of non-isothermal visco-elastic materials and reported that temperature dependent viscosity has a major influence on the variable sheet thickness and final properties of the material in the process. Similarly, Anwar et al. [17] studied non-Newtonian flow of fluids over stretching sheets in porous space and stressed on the effect of thermal conductivity and magnetic fields in changing the pattern of flow and heat transfer rates. Abbas et al. [18] realized the curved surface flow with chemical specieis for non-Newtonian fluids. Nonlinear stretching surfaces play an important impact in transport phenomenon, especially for complex materials. It is reported through some investigative studies that magnetic field, buoyancy and convective boundary conditions play a vital role in flow features and heat transfer characteristics in such systems [19, 20, 21, 22]. These observations are also useful for the industrial processes regarding the nonlinear stretching surface. The Modified Eyring–Powell model is particularly useful in replicating shear-thinning behaviour without developing singularities at zero shear rate as seen in models such as power-law or Bingham. Modified Eyring–Powell model has recently been utilized to consider many engineering problems, such as temperature dependent viscosity in web coating process, non-similar boundary layer flow and heat transfer over a wedge, and chemically reacting nanofluid flow over wedges. These applications demonstrate the model's practical applicability and accuracy in describing the rheological response of the non-Newtonian fluid in various engineering and biomedical practices (see [23, 24, 25]).
Motivated by the above scenario, the present research is pursued to address the impacts of non-Fourier heat flux in Darcy–Forchheimer flow of a Modified Eyring–Powell fluid towards a nonlinear stretching surface with variable thickness. Thermal results are claimed under the assumptions of temperature dependent thermal conductivity. The problem is simplified into dimensionless forms. The homotopy analysis scheme, with excellent accuracy is followed to entertain the simulations.
We investigate a two-dimensional Darcy–Forchheimer flow of a modified Eyring–Powell fluid on a non-linear stretching sheet with variable thickness. The stretching surface starts with a slit placed at the origin with x-axis placed along the sheet and y-axis perpendicular to it. The thermal conductivity is considered as temperature-dependent, and heat diffusion is described using a non-Fourier (Cattaneo–Christov) heat flux model. The surface profile is . The boundary layer assumptions are introduced and the equations of continuity, momentum, and energy written out in the boundary layer coordinate system.
with conditions
The thermal conductivity is assumed to be , where is the thermal conductivity of the ambient fluid, symbolizes a small coefficient for thermal conductivity, and is dimensionless temperature. The constants (b, c, d) have no dimension, and is the dynamic viscosity and the fluid density. The factors B, C, and q are related to the Modified Eyring–Powell (MEP) fluid model. Where is the specific heat, is the fluid temperature, the ambient temperature, and are the velocity components in the , direction, respectively. Following quantities are adopted for simplification:
By the use of Eq. (5) into the Eqs.(2-4), we get
with
Now we have and , then Eq. (7-9) becomes
with
Here and illustrating the fluid parameters, the thermal relaxation parameter and The wall drag force is:
In which
The dimensionless form is
where the local Reynolds number.
The convergent solutions of Eqs. (10) and (11) are solved using the HAM, in the presence of the boundary conditions (5)-(7), (12). The solutions are given in series, consistent with the nature of the problem. The initial guesses and associated linear operators are given by:
Such that
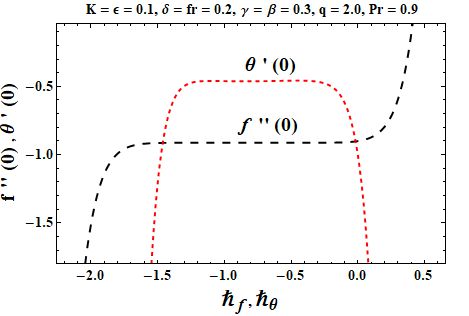
in which elucidate the arbitrary constants. An important part of the HAM method is the H-curve, which presents the convergence of the Eqs. (10) and (11) subject to Eqs. (12). The optimal ranges for the convergence-control parameters are and . The H-curve derived is shown in Figure 1. Table 1 presents accuracy of HAM simulations. The illustration of residual error for HAM has been plotted in Figure 2.
|
||||
|---|---|---|---|---|
| 1 | 0.7182 | 0.7264 | ||
| 6 | 0.7223 | 0.5678 | ||
| 12 | 0.7223 | 0.5691 | ||
| 18 | 0.7223 | 0.5710 | ||
| 24 | 0.7223 | 0.5705 | ||
| 30 | 0.7223 | 0.5705 |
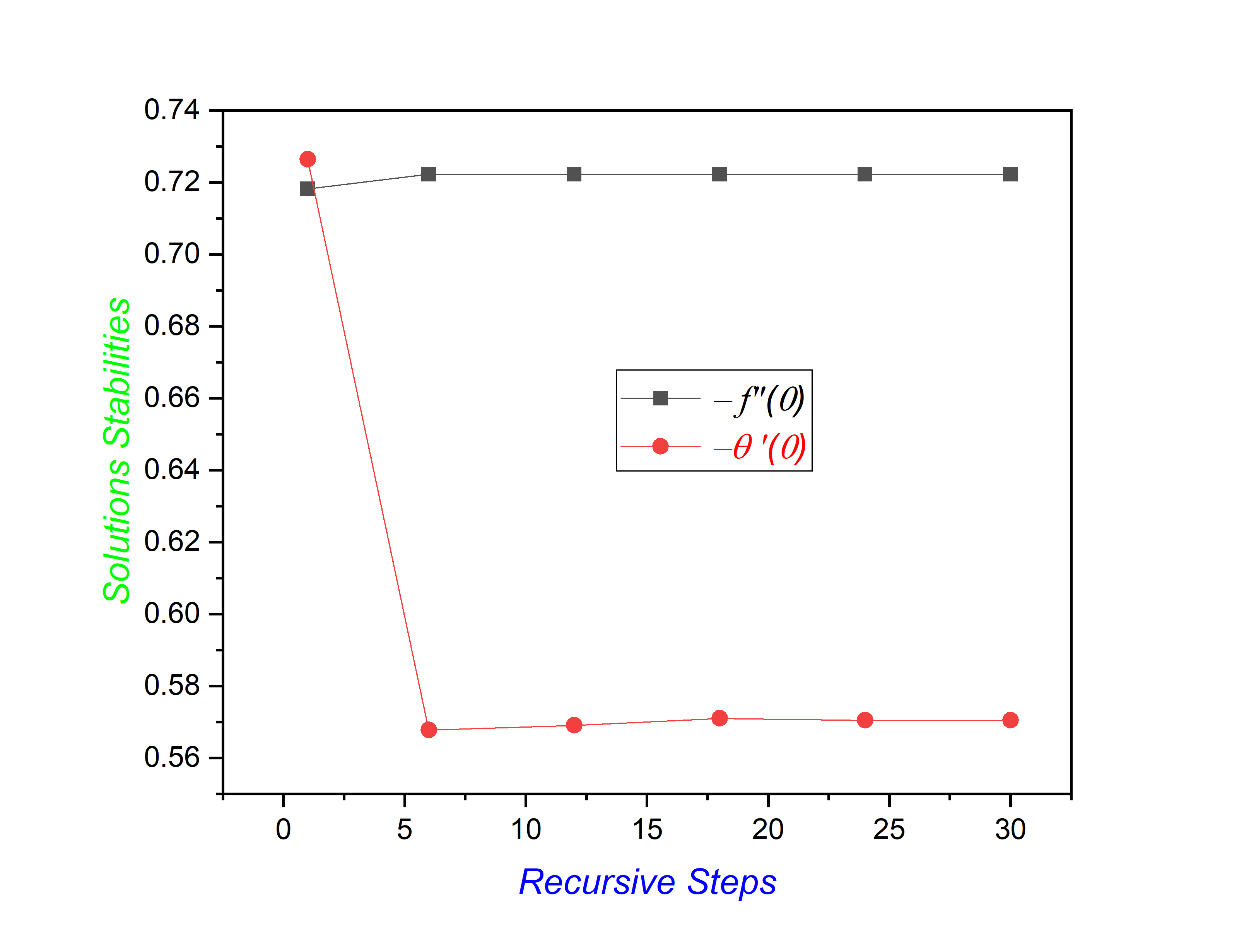
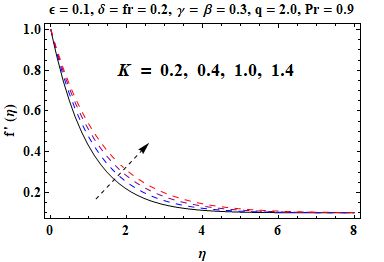
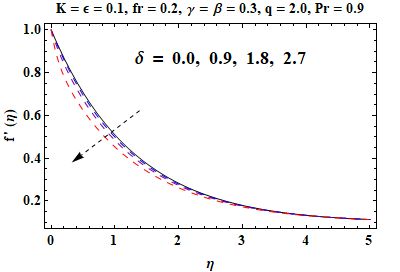
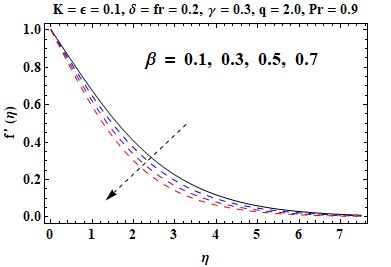
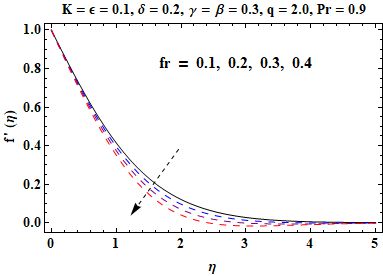
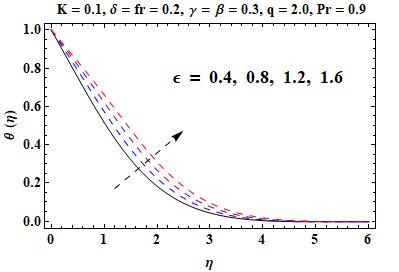
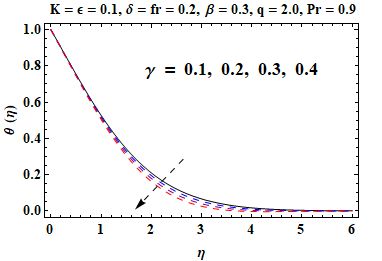
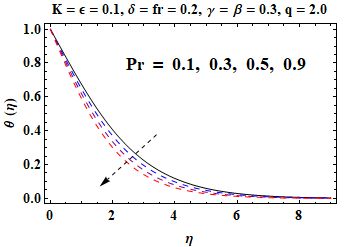
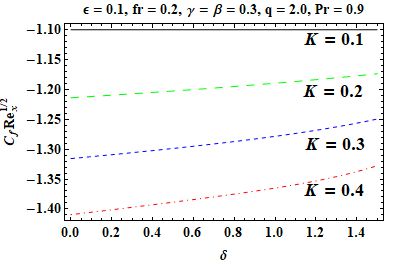
In this section an investigation is made regarding the effects of various parameters on skin friction, velocity and temperature in Figures 3, 4, 5, 6, 7, 8, 9 and 10. Figure 3 shows that when the material parameter becomes larger, the velocity gets increased and the momentum boundary layer thickness becomes thick due to reduction in effective viscosity. In contrast, Figure 4, an increase in the sheet thickness parameter causes a decrease in velocity and the boundary layer thickness. From Figure 5, it can be observed that, with an ascent rate of the porosity parameter , the velocity decreases because of higher resistance in the porous medium. Similarly, Figure 6 demonstrates that at a higher Forchheimer number , inertial effects become more pronounced, which leads to slower flow velocity. Notice from Figure 7 that, temperature increases with increasing thermal conductivity parameter because the higher the value of the thermal conductivity, the more heat is moved from the sheet to the fluid. In Figure 8, the temperature decreases as increases with the maximum heat transfer performance when . It is evident from Figure 9 that, inhibits the thermal boundary layer and temperature profile considerably because of smaller thermal diffusivity. Finally, Figure 10 indicates that skin friction gets enhanced with respect to both and showing stronger shearing effect with the surface as compared to the high value of both these parameters. The homotopic solutions for exhibiting convergence can be seen in Table 1 and the stability of these solutions is shown in Figure 2. A comparison of the skin friction coefficient is given in Table 2, which shows good agreement with available data.
| Turkyilmazoglu [26] | Present | |
| 0.0 | 1.00000 | 1.00000 |
| 0.5 | 1.22474487 | 1.01980 |
| 1.0 | 1.41421356 | 1.11803 |
This work aims to provide a comprehensive analysis of the Darcy–Forchheimer flow of a Modified Eyring–Powell material. Updated heat flux approach is followed to model the problem. The noteworthy observations are:
The velocity decreases as the porosity parameter and Forchheimer number are increased.
Larger material parameter lead to increasing the fluid velocity.
The velocity and corresponding layer thickness decrease with increasing .
Peak variation in temperature rate is assessed due to variable thermal conductivity.
A decrement in wal shear force is observed due to sheet thickness parameter.
 Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. 
Portico
All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/