Heat Transfer and Modified Darcy's Principle in Peristaltic Motion with Hartmann Boundary Layer

Shahid Farooq; Aiman Sana

doi:10.62762/JAM.2025.463651

CiteScore

Impact Factor

Volume 1, Issue 1, ICCK Journal of Applied Mathematics

Volume 1, Issue 1, 2025

Submit Manuscript Edit a Special Issue

Table of Content

1. Introduction
2. Formulation
3. The solution methodology
4. Discussion
5. Concluding remarks

ICCK Journal of Applied Mathematics, Volume 1, Issue 1, 2025: 32-40

Open Access | Research Article | 27 June 2025

Heat Transfer and Modified Darcy's Principle in Peristaltic Motion with Hartmann Boundary Layer

Shahid Farooq 1 *

Aiman Sana 2

1 Department of Mathematics and Statistics, Riphah International University I-14, Islamabad, 44000, Pakistan

2 Department of Mathematics, National University of Modern Languages (NUML), Islamabad 44000, Pakistan

* Corresponding Author: Shahid Farooq, [email protected]

DOI: 10.62762/JAM.2025.463651

Received: 09 May 2025, Accepted: 26 May 2025, Published: 27 June 2025

PDF (2.62 MB) Full-Text HTML XML

Article Metrics Cite This Article

Abstract

This research contains the Hartmann boundary layer effectiveness in peristaltic flow of non-Newtonian viscoelastic fluids through asymmetric channel walls. Due to the Hartmann boundary layer, Hartmann number is considered very large. Porosity effects are included in view of modified Darcy's principle. Energy equation is modelled in the presence of viscous dissipation and Joule heating features. No slip condition for fluid velocity is considered at both channel walls. Large wavelength and dominating viscous forces implementation reduce the PDEs into ODEs. The resulting system of ODEs approximate solution is attained through perturbation and matching techniques for large magnetic field effects. Lastly the obtained approximate analytic solution is utilized to study the varying behaviour of velocity and temperature profiles against involved sundry parameters through graphs.

Keywords

modified darcy law

eyring-powel liquid

heat generation absorption

natural and force convection

compliant wall properties

1. Introduction

The consideration of magnetohydrodynamic (MHD) in moving fluids grabs the attention of researchers due to its attractive and significant usages in physiology and technical industry. Externally applied magnetic field play an important role in drug delivery to targeted points. Flow due to periodic waves propagations becomes more significant in bio medical industry when magnetic field is applied. It is important during bleeding preventions, hyperthermia, ulcer, inflammation etc. treatment. The above mentioned usages of MHD, researchers consider it in peristaltic motion with various aspects. Peristaltically driven flow in the presence of magnetic field and heat transfer of tiny particles is managed by Bhatti et al. [1]. Peristaltic motion of different shape sized nanoparticle with MHD is introduced by Khan et al. [2]. Nanofluid peristaltic movement through an asymmetric channel with entropy generation and MHD is discussed by Ali et al. [3]. Magnetic field is applied in the cilia motion through curved propagating channel with heat exchange is presented by Sadaf and Nadeem [4]. Ali et al. [5] incorporates the Hartmann boundary layer existence in viscoelastic fluid peristaltic movement.

Various clinical and engineering procedures operate via peristaltic mechanisms. It is an inherent property of various physiological organs due to sinusoidal movements of waves e.g. intestine, ureter, lungs, digestive tract, fallopian tube, bile ducts, arteries. Earthworms loco movement is also obeys the peristaltic mechanism. Ceramics and sanitary liquid transport are the industrial applications of peristalsis. Various bio-medical gadgets such as dialysis, heart-lung, blood pressure, nebulizer machines and different clinical injections, coronary bypass, hose pumps are working through mechanism of peristalsis. In light of these applications Latham [6] and Shapiro et al. [7] model and investigates the peristalsis firstly for large wavelength numerically and theoretically. Further Yin and Fung [8, 9] discuss the peristaltic movement through cylindrical ducts. Subsequent studies have advanced peristaltic flow analysis through diverse approaches: Hussain et al. [10] developed a shooting technique for curved radiative flows, while Ranjit et al. [11] quantified entropy generation in electroosmotic microchannels. Numerical innovations include Priam's [12] Casson fluid simulations and Mallick's [13] electromagnetic Eyring-Powell model, complemented by Yasmeen's [14] quantitative/qualitative Jeffrey fluid analysis and Rafiq's [15] Hall/ion-slip nanofluid applications.

The mechanism of heat transfer from lower to higher temperature places is most important and has crucial utilizations in the procedure of haemodialysis and oxygenation. Heat conduction in biological tissues, environmental heat exchangers, cooling system of industrial and mechanical devices, hyperthermia etc. are few more significant examples of heat transfer. Several researchers analyse the characteristics of heat transfer in various physiological liquids transportation. Peristaltic motion with heat transfer was initially investigated by Vajravelu et al. [16] through perpendicular porous tube. Riaz et al. [17] examined fluids irregular motion which is supportive and supply of liquids in a uniform pattern to control temperature fluctuation in the flow field. The complaint properties at wall and transfer of heat under large wavelength and low Reynolds number approximations was studied by Hayat et al. [18]. Another important impulsive resistive situation based on the production of heat transfer when electric current passes through electrically conductive liquid is Joule heating. Hayat et al. [18] examine the transport of liquid through peristaltic principle in a curved configuration with Joule heating, thermal radiation and dissipation features. Magneto Carneau liquid peristaltic flow through curved channel is theoretically examined by Hayat et al. [20]. Shamsuddin et al. [21] incorporates the Joule heating aspects in power-law liquid with slip constraints. Recent advances in peristaltic flows with Joule heating have significantly expanded the theoretical and computational frontiers: Hayat et al. [22] established fundamental slip condition frameworks for nanofluids, while Gireesha et al. [23] quantified entropy generation in inclined microchannels. Geometric innovations emerged through Sucharitha et al.'s [24] flexible wall analyses and Abbasi et al.'s [25] tapered channel radiation models, complemented by Usman et al. [26] and Kodi et al.'s [27] advanced numerical treatments of Riga surfaces and 3D rotational flows. Fractional calculus approaches were advanced by Rubbab et al. [28] using Caputo-Fabrizio operators, synergizing with Rehman et al.'s [29] Jeffery fluid benchmarks and Li et al.'s [30] breakthroughs in activation energy coupling for micropolar nanofluids.

2. Formulation

Here peristalsis on an incompressible and highly electrically conducting Jeffery material through asymmetric configuration. Fluid is flowing because of asymmetric propagation of waves with speed $c$ (see Figure 1). Channel is of width $d_{1}+d_{2}$ . Rectangular coordinates $\overline{X}$ and $\overline{Y}$ are respectively taken along and normal to the asymmetric walls. Magnetic field of large intensity is executed normal to the flow. Permeability effects are encountered through modified Darcy's principle and energy equation comprises the viscous dissipation and Joule heating features.

Figure 1 Flow mechanism.

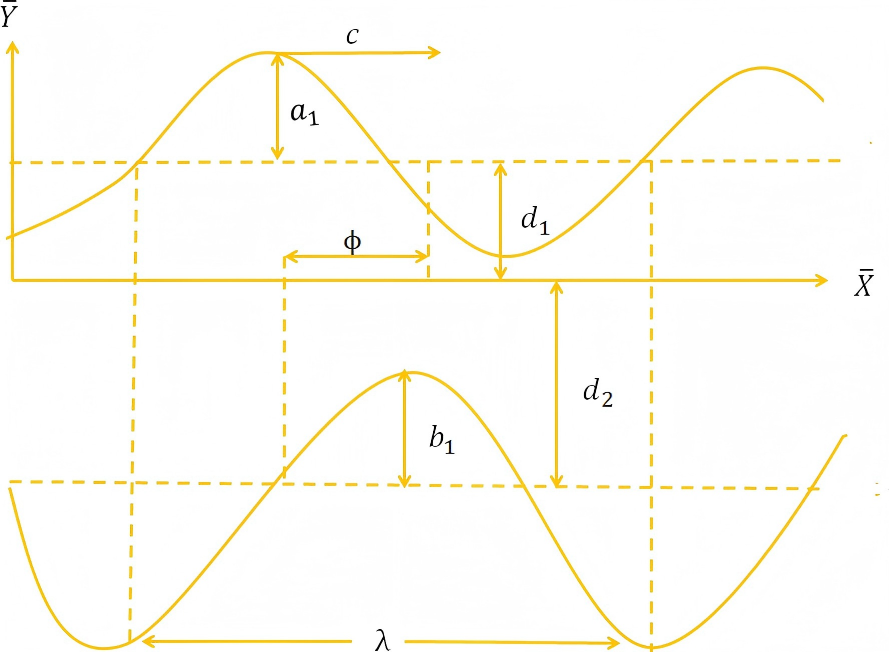
Asymmetric channel walls mathematically are expressed as given below:

\overline{H}_{1}(\overline{X},\overline{t})=d_{1}+a_{1}\cos\left[\frac{2\pi}{% \lambda}\left(\overline{X}-c\overline{t}\right)\right]

\overline{H}_{2}(\overline{X},\overline{t})=-d_{2}-b_{1}\cos\left[\frac{2\pi}{% \lambda}\left(\overline{X}-c\overline{t}\right)+\varphi\right]

Equations which govern the Jeffery fluid flow in compact form are:

\mathrm{div}\overline{\mathbf{V}}=0

\rho\frac{d\overline{\mathbf{V}}}{d\overline{t}}=-\mathrm{grad}\overline{P}+% \mathrm{div}\overline{\mathbf{S}}-\sigma B_{0}^{2}\overline{\mathbf{V}}-\frac{% \mu}{(1+\lambda_{1})}K_{1}\left(1+\lambda_{2}\frac{d}{d\overline{t}}\right)% \overline{\mathbf{V}}

\rho C_{p}\frac{dT}{d\overline{t}}=\kappa\nabla^{2}T+\text{tr}(\overline{% \mathbf{S}}\cdot\overline{\mathbf{L}})+\overline{\mathbf{J}}\cdot\overline{% \mathbf{J}}

where $\mathbf{V}=\left(\overline{U}(\overline{X},\overline{Y},\overline{t}),% \overline{V}(\overline{X},\overline{Y},\overline{t}),0\right),\frac{d}{dt},% \overline{P},\rho,$ and $B_{0},\mathbf{J},\mathbf{L},\mathbf{K}_{1},C_{p}$ denote the velocity field, the material time derivative, the pressure, the fluid density, and the magnetic field strength, current density, velocity gradient, the permeability, and the specific heat capacity respectively. The extra stress tensor $\mathbf{S}$ for Jeffrey fluid is given as follows:

\overline{\mathbf{S}}=\frac{\mu}{1+\lambda_{1}}\left(\overline{\mathbf{A}}_{1}% +\lambda_{2}\frac{d\overline{\mathbf{A}}_{1}}{d\overline{t}}\right)

Eqs. (3) - (5) in expanded form yields:

\frac{\partial\overline{U}}{\partial\overline{X}}+\frac{\partial\overline{V}}{% \partial\overline{Y}}=0

\displaystyle\rho\left[\frac{\partial\overline{U}}{\partial\overline{t}}+% \overline{U}\frac{\partial\overline{U}}{\partial\overline{X}}+\overline{V}% \frac{\partial\overline{U}}{\partial\overline{Y}}\right]=-\frac{\partial% \overline{P}}{\partial\overline{X}}+\frac{\partial\overline{S}_{\overline{X}% \overline{X}}}{\partial\overline{X}}+\frac{\partial\overline{S}_{\overline{XY}% }}{\partial\overline{Y}}

\displaystyle\quad-\sigma B_{0}^{2}\overline{U}-\frac{\mu}{(1+\lambda_{1})}K_{% 1}\left(1+\lambda_{2}\frac{d}{d\overline{t}}\right)\overline{U}

\displaystyle\rho\left[\frac{\partial\overline{V}}{\partial\overline{t}}+% \overline{U}\frac{\partial\overline{V}}{\partial\overline{X}}+\overline{V}% \frac{\partial\overline{V}}{\partial\overline{Y}}\right]=-\frac{\partial% \overline{P}}{\partial\overline{Y}}+\frac{\partial\overline{S}_{\overline{XY}}% }{\partial\overline{X}}+\frac{\partial\overline{S}_{\overline{YY}}}{\partial% \overline{Y}}

\displaystyle\quad-\sigma B_{0}^{2}\overline{V}-\frac{\mu}{(1+\lambda_{1})K_{1% }}\left(1+\lambda_{2}\frac{d}{d\overline{t}}\right)\overline{V}

\displaystyle\rho C_{p}\frac{dT}{d\overline{t}}=K\left(\frac{\partial^{2}T}{% \partial\overline{X}^{2}}+\frac{\partial^{2}T}{\partial\overline{Y}^{2}}\right% )+S_{\overline{XX}}\frac{\partial\overline{U}}{\partial\overline{X}}+\overline% {S}_{\overline{YY}}\frac{\partial\overline{V}}{\partial\overline{Y}}

\displaystyle\quad+S_{\overline{XY}}\left(\frac{\partial\overline{U}}{\partial% \overline{Y}}+\frac{\partial\overline{V}}{\partial\overline{X}}\right)+\sigma B% _{0}^{2}\overline{U}^{2}

Conditions at boundaries are taken in the form at

\overline{U}=0,\quad T-T_{1}\quad\text{at}\quad\overline{Y}=\overline{H}_{1}

\overline{U}=0,\quad T-T_{0}\quad\text{at}\quad\overline{Y}=\overline{H}_{2}

Stress components are

S_{\overline{X}\overline{X}}=\frac{2\mu}{1+\lambda_{1}}\left[\lambda_{2}\left(% \frac{\partial}{\partial\overline{t}}+\overline{U}\frac{\partial}{\partial% \overline{X}}+\overline{V}\frac{\partial}{\partial\overline{Y}}\right)+1\right% ]\frac{\partial\overline{U}}{\partial\overline{X}}

S_{\overline{Y}\overline{Y}}=\frac{2\mu}{1+\lambda_{1}}\left[\lambda_{2}\left(% \frac{\partial}{\partial\overline{t}}+\overline{U}\frac{\partial}{\partial% \overline{Y}}+\overline{V}\frac{\partial}{\partial\overline{Y}}+1\right)\right% ]\frac{\partial\overline{V}}{\partial\overline{Y}}

S_{\overline{X}\overline{Y}}=\frac{2\mu}{1+\lambda_{1}}\left[\lambda_{2}\left(% \frac{\partial}{\partial\overline{t}}+\overline{U}\frac{\partial}{\partial% \overline{X}}+\overline{V}\frac{\partial}{\partial\overline{Y}}\right)+1\right% ]\left(\frac{\partial\overline{U}}{\partial\overline{Y}}+\frac{\partial% \overline{V}}{\partial\overline{X}}\right)

To transform the system (7-15), the following relation between fixed and moving frames are utilized.

\displaystyle\bar{x}=\overline{X}-c\overline{t},\quad\bar{y}=\overline{Y},% \quad u(\bar{x},\bar{y})=\overline{U}(\overline{X},\overline{Y},\overline{t})-c,

\displaystyle v(\bar{x},\bar{y})=\overline{V}(\overline{X},\overline{Y},% \overline{t}),\quad p(\bar{x},\bar{y})=\overline{P}(\overline{X},\overline{Y},% \overline{t})

Variables in dimensionless are defined as:

\displaystyle x=\frac{2\pi\bar{x}}{\lambda},\quad y=\frac{\bar{y}}{d_{1}},% \quad u=\frac{\bar{u}}{c},\quad v=\frac{\bar{v}}{c},\quad

\displaystyle\theta=\frac{T-T_{0}}{T_{1}-T_{0}},\quad S_{ij}=\frac{d_{1}}{c\mu% }\,\overline{S}_{\bar{i}\bar{j}}

Relation between dimensionless velocity component and stream function is

u=\frac{\partial\psi}{\partial y},\quad v=-\delta\frac{\partial\psi}{\partial x}.

Using fixed to wave frame transformations (16), dimensionless variables (17) and velocities in terms of stream suction (18) Eqs. (7) satisfied identically and the other expressions takes the following form:

\displaystyle\delta\,\text{Re}\Bigg{[}\left(\frac{\partial\psi}{\partial y}% \frac{\partial}{\partial x}-\frac{\partial\psi}{\partial x}\frac{\partial}{% \partial y}\right)\left(\frac{\partial\psi}{\partial x}\right)\Bigg{]}+\frac{% \partial p}{\partial x}=\delta\frac{\partial S_{xx}}{\partial x}+\frac{% \partial S_{xy}}{\partial x}

\displaystyle-M^{2}\left(\frac{\partial\psi}{\partial y}+1\right)-\frac{1}{D_{% a}K_{1}(1+\lambda_{1})}\Bigg{[}\left(\frac{\partial\psi}{\partial y}+1\right)+

\displaystyle c\frac{\lambda_{2}}{d_{1}}\left(\delta\frac{\partial^{2}\psi}{% \partial y^{2}}\frac{\partial}{\partial x}-\delta\frac{\partial^{2}\psi}{% \partial x^{2}}\frac{\partial}{\partial y}\right)\Bigg{]}.

\displaystyle-\delta^{3}\,\text{Re}\Bigg{[}\left(\frac{\partial\psi}{\partial y% }\frac{\partial}{\partial x}-\frac{\partial\psi}{\partial x}\frac{\partial}{% \partial y}\right)\left(\frac{\partial\psi}{\partial x}\right)\Bigg{]}+\frac{% \partial p}{\partial y}=\delta^{2}\frac{\partial S_{xy}}{\partial x}

\displaystyle+\delta\frac{\partial S_{yy}}{\partial y}+M^{2}\delta\frac{% \partial\psi}{\partial x}-\frac{\delta}{D_{a}K_{1}(1+\lambda_{1})}\Bigg{[}-% \delta\frac{\partial\psi}{\partial x}

\displaystyle+\frac{\lambda_{2}}{d_{1}}\Bigg{(}-\delta^{2}\frac{\partial^{2}% \psi}{\partial x\partial y}-\delta\frac{\partial^{2}\psi}{\partial y^{2}}\Bigg% {)}\Bigg{]}

\displaystyle\text{Re}\,\delta\Bigg{[}\left(\frac{\partial\psi}{\partial y}% \frac{\partial\theta}{\partial x}-\frac{\partial\psi}{\partial x}\frac{% \partial\theta}{\partial y}\right)\Bigg{]}=\frac{1}{Pr}\left(\delta\frac{% \partial^{2}\theta}{\partial x^{2}}+\frac{\partial^{2}\theta}{\partial y^{2}}\right)

\displaystyle+\delta E_{c}S_{xx}\frac{\partial\psi}{\partial x\partial y},-% \delta E_{c}S_{xy}\frac{\partial\psi}{\partial x}+E_{c}M^{2}\left(\frac{% \partial\psi}{\partial y}+1\right)^{2}+\delta\frac{\partial u}{\partial x}

\displaystyle+\delta\frac{\partial v}{\partial x}+E_{c}S_{xy}\left(\frac{% \partial u}{\partial y}+\delta\frac{\partial v}{\partial x}\right)

\displaystyle S_{xx}=\frac{2\delta}{1+\lambda_{1}}\left[1+\delta\lambda_{2}% \left(\frac{\partial\psi}{\partial y}\frac{\partial}{\partial x}-\frac{% \partial\psi}{\partial x}\frac{\partial}{\partial y}\right)\right]

\displaystyle\times\frac{\partial}{\partial x}\left(\frac{\partial\psi}{% \partial y}\right)

\displaystyle S_{xy}=\frac{1}{1+\lambda_{1}}\left[1+\delta\lambda_{2}\left(% \frac{\partial\psi}{\partial y}\frac{\partial}{\partial x}-\frac{\partial\psi}% {\partial x}\frac{\partial}{\partial y}\right)\right]

\displaystyle\times\left(\frac{\partial}{\partial y}\left(\frac{\partial\psi}{% \partial y}\right)-\delta^{3}\frac{\partial}{\partial x}\left(\frac{\partial% \psi}{\partial x}\right)\right)

\displaystyle S_{yy}=\frac{-2\delta}{1+\lambda_{1}}\left[1+\lambda_{2}\delta% \left(\frac{\partial\psi}{\partial y}\frac{\partial}{\partial x}-\frac{% \partial\psi}{\partial x}\frac{\partial}{\partial y}\right)\right]

\displaystyle\times\frac{\partial}{\partial y}\left(\frac{\partial\psi}{% \partial x}\right).

Dimensionless numbers arises in Eqs. (19-24) are defined as

\displaystyle p=\frac{2\pi d_{1}^{2}\bar{p}}{c\lambda\mu},\quad h_{1}=\frac{% \bar{h_{1}}}{d_{1}},\quad h_{2}=\frac{\bar{h_{2}}}{d_{2}},\quad\delta=\frac{2% \pi d_{1}}{\lambda},

\displaystyle Re=\frac{\rho cd_{1}}{\mu},\quad M^{2}=\frac{\sigma B_{0}^{2}d_{% 1}^{2}}{\mu},

\displaystyle a=\frac{a_{1}}{d_{1}},\quad b=\frac{b_{1}}{d_{1}},\quad d=\frac{% d_{2}}{d_{1}},\quad E_{c}=\frac{c^{2}}{(T_{1}-T_{0})c_{p}},

\displaystyle P_{r}=\frac{\mu c_{p}}{K},\quad D_{a}=\frac{d^{2}}{K_{1}}.

Boundary conditions becomes

\psi=\frac{q}{2},\quad\psi^{\prime}=-1,\quad\theta=1,\quad\text{at}\quad y=h_{% 1}.

\psi=-\frac{q}{2},\quad\psi^{\prime}=-1,\quad\theta=0,\quad\text{at}\quad y=h_% {2}.

3. The solution methodology

Eqs. (19–24) yields after employing dominating large viscous forces (i.e., Re $\ll$ 1) and wavelength (i.e., $\delta\ll$ 1) conditions:

\frac{\partial p}{\partial x}=\frac{\partial S_{xy}}{\partial y}-\left(M^{2}+% \frac{1}{D_{a}(1+\lambda_{1})}\right)\left(\frac{\partial\psi}{\partial y}+1\right)

\frac{\partial p}{\partial y}=0

\frac{1}{P_{r}}\left(\frac{\partial^{2}\theta}{\partial y^{2}}\right)+E_{c}% \left[S_{xy}\frac{\partial u}{\partial y}+M^{2}\left(\frac{\partial\psi}{% \partial y}+1\right)^{2}\right]=0

S_{xy}=\frac{1}{1+\lambda_{1}}\left(\frac{\partial}{\partial y}\left(\frac{% \partial\psi}{\partial y}\right)\right)

where $S_{xy}$ is given in Eq. (31). After using the cross differentiation technique, Eqs. (28 and 29) yields.

\frac{\partial^{4}\psi}{\partial y^{4}}-\left[M^{2}(1+\lambda_{1})+\frac{1}{D_% {a}}\right]\frac{\partial^{2}\psi}{\partial y^{2}}=0

In this chapter we use the similar methodology (i.e asymptotic analysis) to evaluate Eq. (32) with respective boundary conditions. Using this solution Eq. (30) with respective boundary condition is solved numerically through ND Solve command in Mathematica 9.0.

3.1 Asymptotic approximation for large magnetic field(𝐌)

For large $\mathbf{M}$ approximate solution is obtained away and adjacent to the channel boundaries and then match it with solution at the edges of boundaries. After that a uniform composite solution is obtained.

3.2 The outer solution

Express Eq.(32) in terms of Eq.(33) to evaluate asymptotic solution for very large $\mathbf{M}$ .

\psi(y)=\psi_{0}+\epsilon\psi_{1}

where $M=\frac{1}{\epsilon}$ and $\frac{1}{D_{a}}=\frac{1}{\epsilon}$ where $\epsilon\ll 1$ . Then the leading order equation of Eq. (32) and its solution is:

(2+\lambda_{1})\frac{\partial^{2}\psi_{0}}{\partial y^{2}}=0

\psi_{0}(y)=a_{0}y+b_{0}

Similarly, the first order equation and its solution is:

\frac{\partial^{4}\psi_{0}}{\partial y^{4}}-(2+\lambda_{1})\frac{\partial^{2}% \psi_{1}}{\partial y^{2}}=0

\psi_{1}(y)=a_{1}y+b_{1}

Combining Eqs. (34 and 36), the asymptotic solution up to order $\epsilon$ is:

\psi^{\text{out}}(y)=a_{0}y+b_{0}+\epsilon\left(a_{1}y+b_{1}\right)

where $a_{0}$ , $b_{0}$ , $a_{1}$ and $b_{1}$ can be calculated through comparing the higher order term of inner and outer solutions. Here we evaluate two inner solutions to attain a valid and uniform solution at two boundaries because outer solution is not valid at $o(\epsilon)$ .

3.3 The inner solutions

(i) For inner solution at $y=h_{1}$ , Eq. (32), the solution near to the boundary at $y=h_{1}(x)$ , the stretched variable is in the form $\eta=\frac{h_{1}-y}{\epsilon^{p}}$ yields:

\epsilon^{2-4p}\frac{\partial^{4}\psi^{in}}{\partial\eta^{4}}-(1+\lambda_{1})% \epsilon^{-2p}\frac{\partial^{2}\psi^{in}}{\partial\eta^{2}}-\epsilon^{-2p}% \frac{\partial^{2}\psi^{in}}{\partial\eta^{2}}=0

Taking $p=1$ in view of least degeneracy condition to balance the solution of Eq. (39) because viscosity effects must be present in inner solution.

\frac{\partial^{4}\psi^{in}}{\partial\eta^{4}}-k\frac{\partial^{2}\psi^{in}}{% \partial\eta^{2}}=0

in which Eq. (40), $K=2+\lambda_{1}$ . The condition at $y=h_{1}$ boundary becomes:

\psi^{in}(\eta)=\frac{q}{2}\quad\text{and}\quad\frac{\partial\psi^{in}}{% \partial\eta}(\eta)=\epsilon\quad\text{at}\quad\eta=0

The two term solution of Eq.(40) is assumed as

\psi^{in}(\eta)=\psi_{0}^{in}(\eta)+\epsilon\psi_{1}^{in}(\eta)

where Zeroth order system and its solution is of the form:

\frac{\partial^{4}\psi_{0}^{in}}{\partial\eta^{4}}-k\frac{\partial^{2}\psi_{0}% ^{in}}{\partial\eta^{2}}=0

\psi_{0}^{in}(0)=\frac{q}{2},\quad\frac{\partial\psi_{0}^{in}}{\partial\eta}(0% )=0

\psi_{0}^{in}=\frac{q}{2}+D_{0}\left(-1+\sqrt{k\eta}+e^{-\sqrt{k\eta}}\right)

The two term inner solution at $y=h_{1}$ is obtained by putting Eqs. (45 and 48) in $\psi^{in}(\eta)=\psi_{0}^{in}(\eta)+\epsilon\psi_{1}^{in}(\eta)$ , we get:

\displaystyle\psi_{2}^{in}=\frac{q}{2}+D_{0}\left(-1+\sqrt{k\eta}+e^{-\sqrt{k% \eta}}\right)

\displaystyle\quad+\epsilon\left[\eta+D_{1}\left(-1+\sqrt{k\eta}+e^{-\sqrt{k% \eta}}\right)\right]

(ii) In similar manner the two term inner solution is found at $y=h_{2}$ by using $\zeta=\frac{y-h_{2}}{\epsilon}$ in Eq. (39).

\displaystyle\psi_{2}^{\sim in}(\zeta)=-\frac{q}{2}+H_{0}\left(-1+\sqrt{k}% \zeta+e^{-\sqrt{k}\zeta}\right)

\displaystyle\quad+\epsilon\left[-\zeta+H_{1}\left(-1+\sqrt{k}\zeta+e^{-\sqrt{% k}\zeta}\right)\right]

The values of all constants appearing in Eqs.(49 and 50) is found by comparing inner and outer solutions at both walls.

3.4 The higher order mode matching

To employ higher order mode of matching procedure use an intermediate variable $t$ given in Eq. (50) at $y=h_{1}$ in the intermediate location $o(\epsilon^{\alpha})$ . Two terms inner and outer solution in the form of variable $t$ at $y=h_{1}$ by neglecting the terms higher than $\epsilon^{\alpha+1}$ and greater after converting the outer and inner solutions into intermediate parameter $t$ at lower plate yields:

\left(\psi^{\text{out}}\right)^{\text{int}}=a_{0}h_{1}+b_{0}-a_{0}t(\epsilon)^% {\alpha}+\epsilon\left(a_{1}h_{1}+b_{1}\right)+o(\epsilon^{\alpha+1})

\left(\psi^{\text{in}}\right)^{\text{int}}=\frac{q}{2}+D_{0}\left(-1+kt(% \epsilon)^{\alpha-1}\right)+t(\epsilon)^{\alpha}\left(1+kD_{1}\right)-D_{1}\epsilon

implies:

\displaystyle a_{0}h_{1}+b_{0}=\frac{q}{2}-D_{0},\quad D_{0}=0,

\displaystyle 1+\sqrt{k}D_{1}=-a_{0},\quad a_{1}h_{1}+b_{1}=-D_{1}

Similarly at upper plate $y=h_{2}(x)$ , matching of outer and inner solutions is:

\displaystyle a_{0}h_{2}+b_{0}=-\frac{q}{2}-H_{0},\quad H_{0}=0,

\displaystyle-1+\sqrt{k}H_{1}=a_{0},\quad a_{1}h_{2}+b_{1}=-H_{1}

Eq.(53) and Eq.(54) are evaluated simultaneously to obtain the unknown constants:

\displaystyle a_{0}=\frac{q}{h_{1}-h_{2}}

\displaystyle a_{1}=\frac{2}{\sqrt{k}(h_{1}-h_{2})}\left(1+\frac{q}{h_{1}-h_{2% }}\right)

\displaystyle b_{0}=-\frac{q}{2}\left(\frac{h_{1}+h_{2}}{h_{1}-h_{2}}\right)

\displaystyle b_{1}=-\frac{1}{\sqrt{k}}\left(\frac{h_{1}+h_{2}}{h_{1}-h_{2}}% \right)\left(1+\frac{q}{h_{1}-h_{2}}\right)

\displaystyle H_{1}=\frac{1}{\sqrt{k}}\left(1+\frac{q}{h_{1}-h_{2}}\right)

The composite solution can be expressed as:

\psi_{\text{composite}}=\psi^{\text{out}}+\psi^{\text{in}}(\eta)-\left(\psi^{% \text{int}}\right)^{\text{in}}+\psi^{\sim\text{int}}(\zeta)-\left(\psi^{\sim% \text{int}}\right)

Now, using Eq.(49), Eq. (50) and Eqs. (51,52) into Eq. (56), the composite solution is finally given by:

\displaystyle\psi_{\text{composite}}=\frac{qy}{h_{1}-h_{2}}-\frac{q}{2}\left(% \frac{h_{1}+h_{2}}{h_{1}-h_{2}}\right)

\displaystyle\quad+\frac{\epsilon}{\sqrt{k}}\left(1+\frac{q}{h_{1}-h_{2}}% \right)\times

\displaystyle\quad\left[\frac{2y}{h_{1}-h_{2}}-\frac{h_{1}+h_{2}}{h_{1}-h_{2}}% e^{\sqrt{k}\frac{h_{1}-y}{\epsilon}}+e^{-\sqrt{k}\frac{y-h_{2}}{\epsilon}}\right]

The composite solution presented in Eq. (57) is completely valid for all independent variable values which fulfills the accounted boundary conditions.

4. Discussion

The goal of this section is to study the graphical behaviour of velocity and temperature profiles against Darcy number $D a$ , Hartmann number ( $M$ ), Jeffery fluid parameters $\lambda_{1}$ and Brinkmann number $B r$ .

4.1 Velocity Profile

Figure 2

u

D a

for

B r

= 0.2;

x

= 0;

M

= 1.0;

\lambda_{1}

= 0.5;

\alpha

= 0.02;

\beta

= 0.02.

Figure 3

u

\lambda_{1}

for

B r

= 0.2;

x

= 0;

M

= 1.0;

D a

= 0.5;

\alpha

= 0.02;

\beta

= 0.02 .

Figure 4

u

M

for

B r

=0.2;

x

=0;

D a

=0.5;

\lambda_{1}

=0.5;

\alpha

=0.01;

\beta

=0.02.

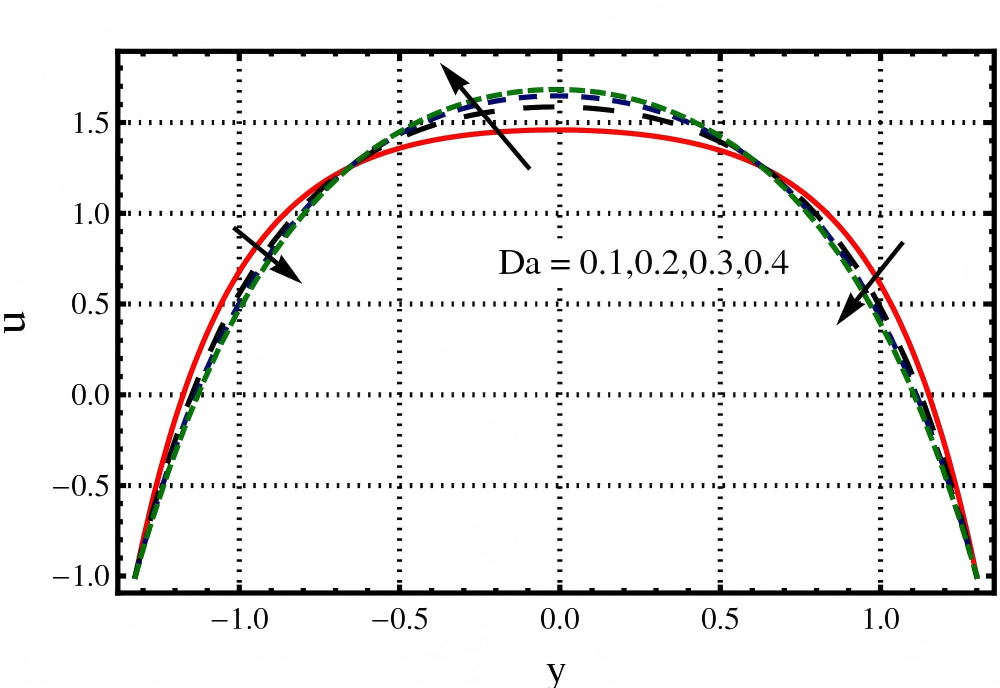
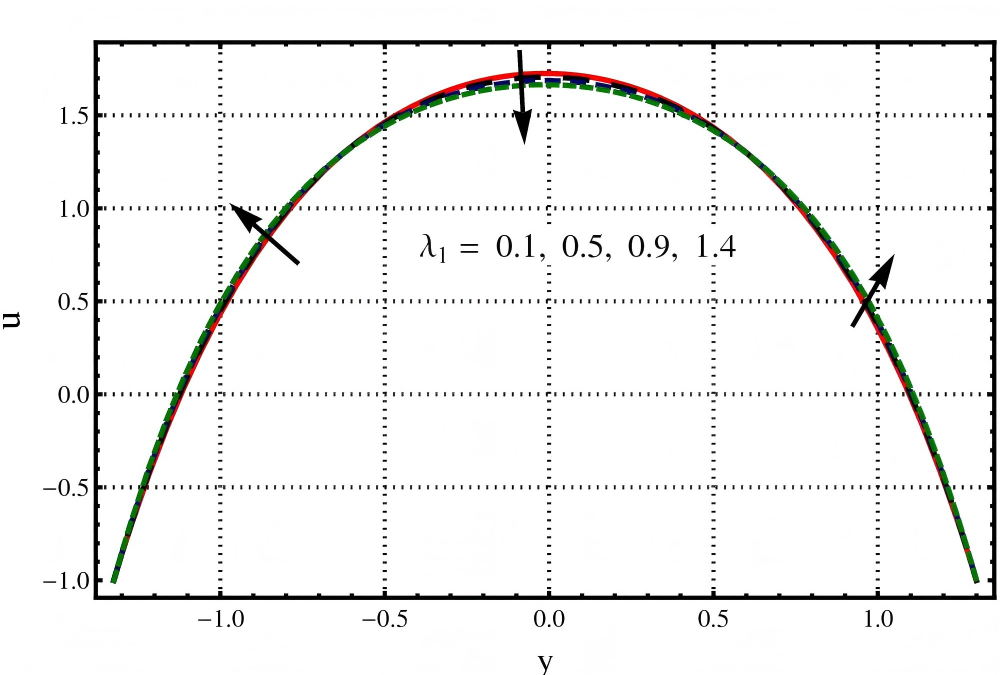
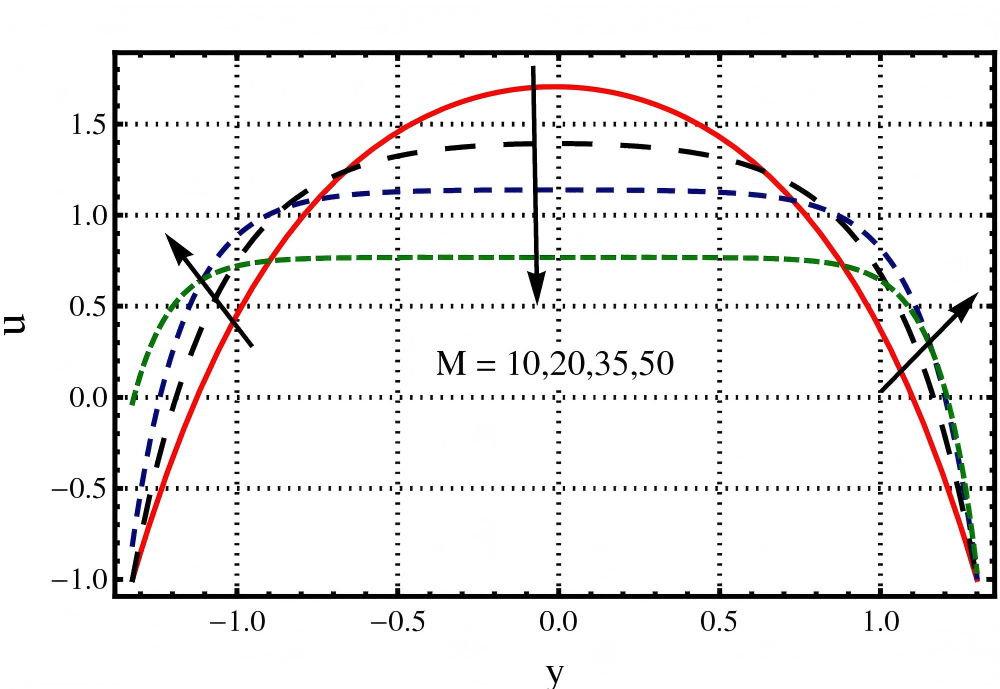
The impact of $D a$ , $M$ and $\lambda_{1}$ on velocity profile are captured in Figures 2, 3 and 4. The velocity of flowing fluid increases with an increase in Darcy number ( $D a$ ) as graphically presented in Figure 2. When studying peristaltic flow through veins and arteries, the porosity of walls must be considered. Because an increase in porosity causes a reduction in drag force gives a resulting decrease in flow resistance. The decrease in velocity towards the channel boundaries is also observed in this Figure 3 depicts that an increase in the value of Jeffery fluid parameter ( $\lambda_{1}$ ) causes a reduction in velocity. It is because by increasing $\lambda_{1}$ the viscous effects dominate at the centre of the channel. Due to the classical effect of Hartmann number, it is obvious that an increase in the value of $M$ causes a decrease in velocity profile as illustrated in Figure 4. As Lorentz force (a resistive force) is present in MHD phenomena, thus by increasing $M$ the Lorentz force produce more resistance to the fluid flow due to which velocity decreases.

Figure 5 Temperature profile of

D a

for

B r

=0.2;

x

=0;

M

=1.0;

\lambda_{1}

=0.5;

\alpha

=0.02;

\beta

=0.02.

Figure 6 Temperature profile of

\lambda_{1}

for

B r

=0.2;

x

=0;

M

=1.0;

D a

=0.5;

\alpha

=0.01;

\beta

=0.02.

Figure 7 Temperature profile of

M

for

B r

=0.2;

x

=0;

D a

=0.5;

\lambda_{1}

=0.5;

\alpha

=0.01;

\beta

=0.02.

Figure 8 Temperature profile of

B r

for

x

=0;

M

=1.0;

D a

=0.5;

\lambda_{1}

=0.5;

\alpha

=0.01;

\beta

=0.02.

4.2 Temperature Profile

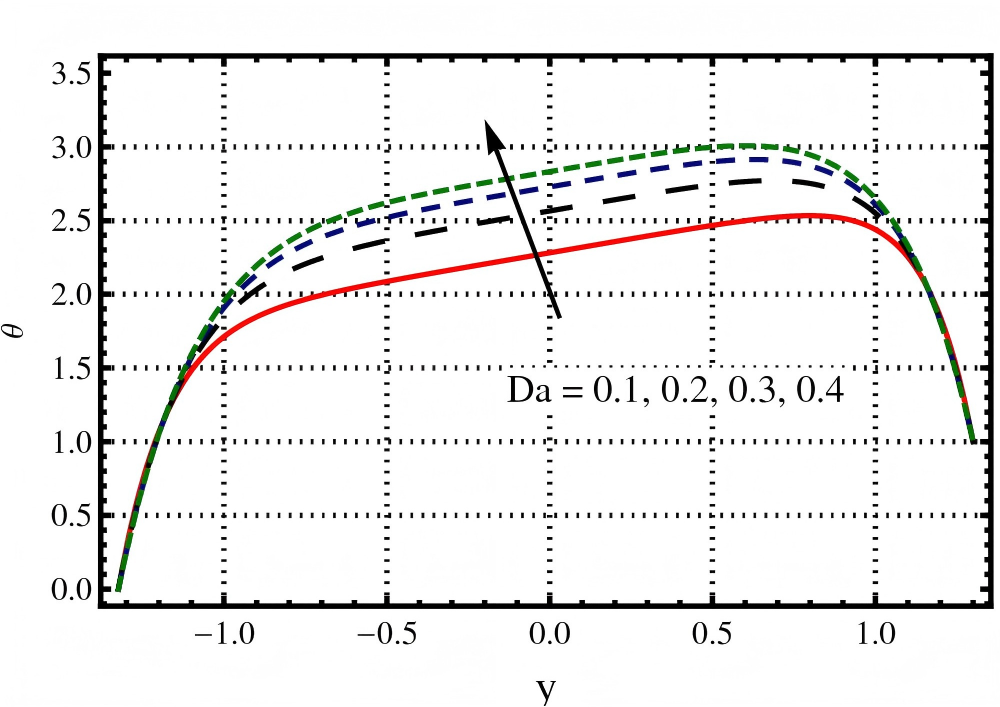
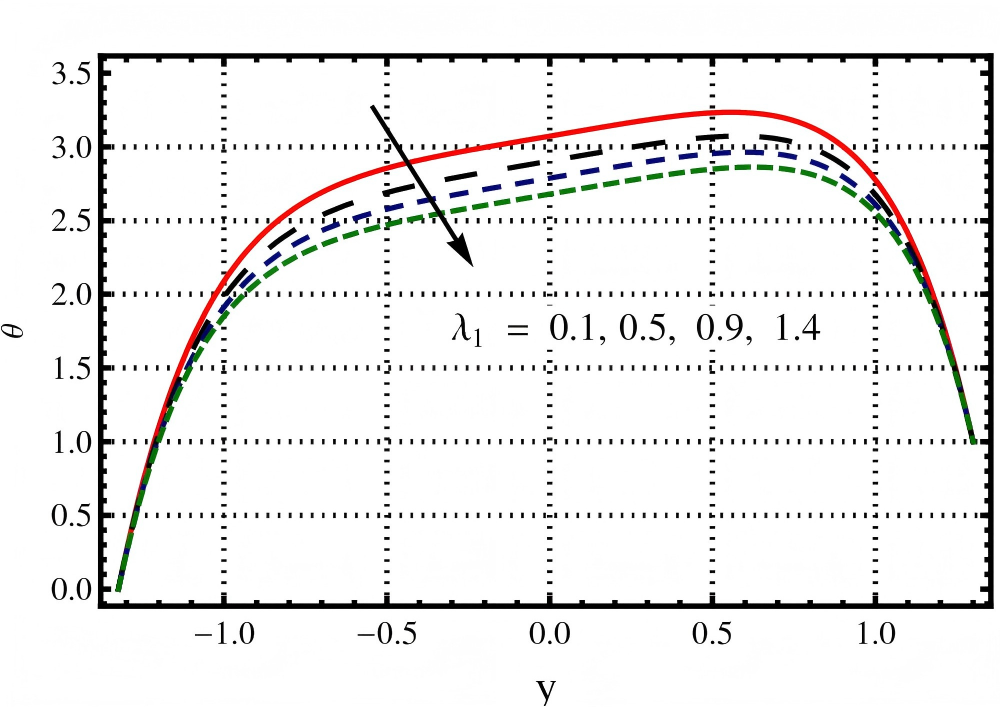
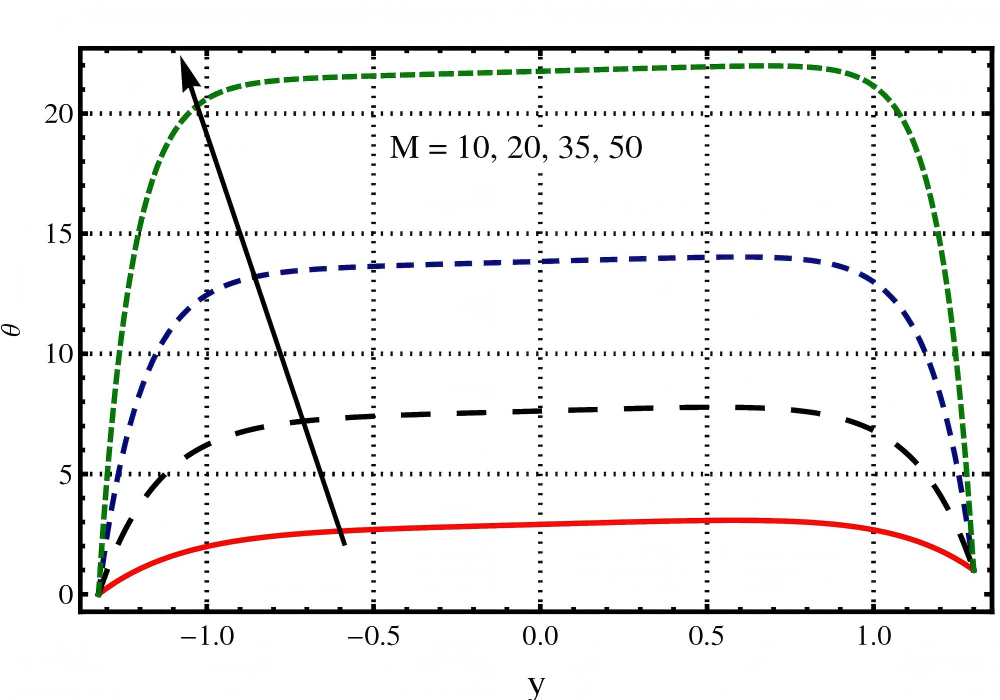
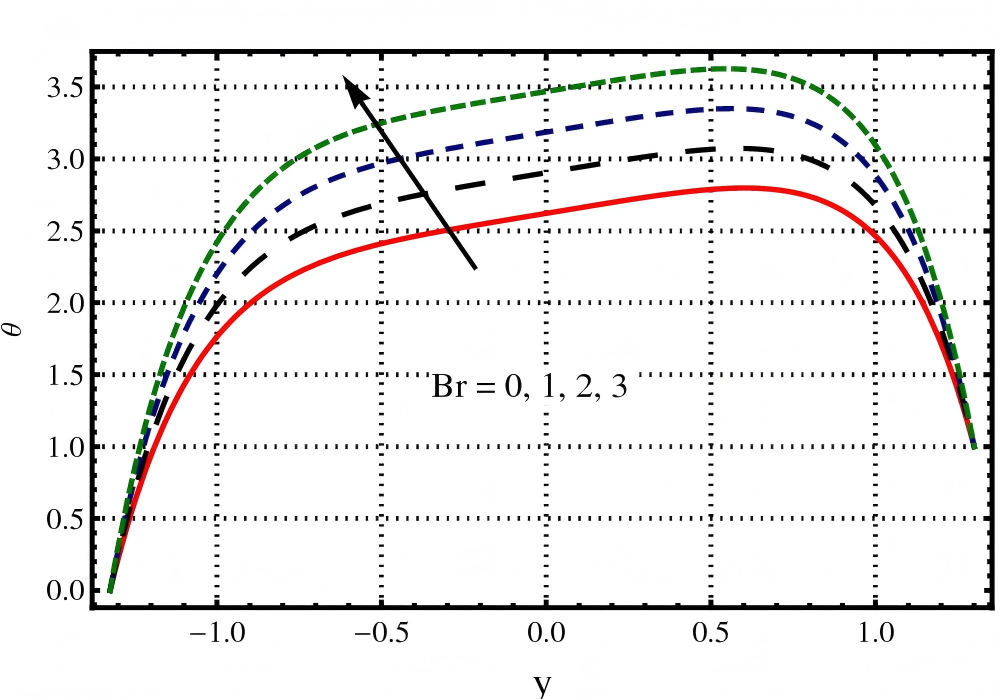
The impact of $D a$ , $M$ , $\lambda_{1}$ , $B r$ on temperature profile (a resistive force) through Figures 5, 6, 7 and 8. In this section it is observed from Figure 5 that the profile for temperature distribution increases with an increase in the value of Darcy number ( $D a$ ). Figure 6 depicts that an increase in the value of Jeffery fluid parameter ( $\lambda_{1}$ ) causes a reduction in temperature. Figure 7 depicts that higher increase in the value of Hartmann number ( $M$ ) causes an increase in temperature. Figure 8 depicts that an increase in the value of Brinkman number ( $B r$ ) causes an increase in temperature. It is observed through these Figures 5, 6, 7 and 8 that temperature increases because of resistive characteristics of $D a$ , $M$ , and $B r$ parameters.

5. Concluding remarks

The key findings of this study are: 1. The velocity changes for modified Darcy parameter. 2. The Hartmann boundary layer increases for increasing $M$ . 3. For higher $\lambda_{1}$ temperature decays. 4. Both Magnetic and Darcy parameter enhances the temperature.

Data Availability Statement

Data will be made available on request.

Funding

This work was supported without any funding.

Conflicts of Interest

The authors declare no conflicts of interest.

Ethical Approval and Consent to Participate

Not applicable.

References

Bhatti, M. M., Zeeshan, A., Ijaz, N., & Ellahi, R. (2017). Heat transfer and inclined magnetic field analysis on peristaltically induced motion of small particles. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 39(8), 3259–3267.
[CrossRef] [Google Scholar]
Khan, L. A., Raza, M., Mir, N. A., & Ellahi, R. (2020). Effects of different shapes of nanoparticles on peristaltic flow of MHD nanofluids filled in an asymmetric channel. Journal of Thermal Analysis and Calorimetry, 140(2), 879–890.
[CrossRef] [Google Scholar]
Ali, A., Shah, Z., Mumraiz, S., Kumam, P., & Awais, M. (2019). Entropy generation on MHD peristaltic flow of Cu-water nanofluid with slip conditions. Heat Transfer—Asian Research, 48(8), 4301–4319.
[CrossRef] [Google Scholar]
Sadaf, H., & Nadeem, S. (2020). Fluid flow analysis of cilia beating in a curved channel in the presence of magnetic field and heat transfer. Canadian Journal of Physics, 98(2), 191-197.
[CrossRef] [Google Scholar]
Ali, A., Awais, M., Zubaidi, A., Saleem, S., & Marwat, D. N. K. (2022). Hartmann boundary layer in peristaltic flow for viscoelastic fluid: Existence. Ain Shams Engineering Journal, 13(2), 101555.
[CrossRef] [Google Scholar]
Akbar, N. S., & Butt, A. W. (2015). Heat transfer analysis of peristaltic flow in a curved channel. International Journal of Heat and Mass Transfer, 85, 762-767.
[CrossRef] [Google Scholar]
Shapiro, A. H., Jaffrin, M. Y., & Weinberg, S. L. (1969). Peristaltic pumping with long wavelengths at low Reynolds number. Journal of Fluid Mechanics, 37(4), 799–825.
[CrossRef] [Google Scholar]
Fung, Y. C., & Yin, C. S. (1968). Peristaltic transport. ASME Journal of Applied Mechanics, 35(4), 699–1675.
[CrossRef] [Google Scholar]
Yin, F., & Fung, Y. C. (1969). Peristaltic waves in circular cylindrical tubes. ASME Journal of Applied Mechanics, 36(4), 579–587.
[CrossRef] [Google Scholar]
Hussain, Z., Khaled, K., Sharif, U., Abbasi, A., Khan, S. U., Farooq, W., ... & Malik, M. Y. (2022). A mathematical model for radiative peristaltic flow of Jeffrey fluid in curved channel with Joule heating and different walls: Shooting technique analysis. Ain Shams Engineering Journal, 13(5), 101685.
[CrossRef] [Google Scholar]
Ranjit, N. K., Shit, G. C., & Tripathi, D. (2019). Entropy generation and Joule heating of two layered electroosmotic flow in the peristaltically induced micro-channel. International Journal of Mechanical Sciences, 153–154, 430–444.
[CrossRef] [Google Scholar]
Priam, S. S., & Nasrin, R. (2022). Numerical appraisal of time-dependent peristaltic duct flow using Casson fluid. International Journal of Mechanical Sciences, 233, 107676.
[CrossRef] [Google Scholar]
Mallick, B., & Misra, J. C. (2018). Peristaltic flow of Eyring-Powell nanofluid under the action of an electromagnetic field. Engineering Science and Technology, an International Journal, 22(1), 266–281.
[CrossRef] [Google Scholar]
Yasmeen, S., Asghar, S., Anjum, H. J., & Ehsan, T. (2019). Analysis of Hartmann boundary layer peristaltic flow of Jeffrey fluid: Quantitative and qualitative approaches. Communications in Nonlinear Science and Numerical Simulation, 76, 51–65.
[CrossRef] [Google Scholar]
Rafiq, M., Yasmin, H., Hayat, T., & Alsaadi, F. (2019). Effect of Hall and ion-slip on the peristaltic transport of nanofluid: A biomedical application. Chinese Journal of Physics, 60, 208–227.
[CrossRef] [Google Scholar]
Vajravelu, K., Radhakrishnamacharya, G., & Radhakrishnamurty, V. (2007). Peristaltic flow and heat transfer in a vertical porous annulus, with long wave approximation. International Journal of Non-Linear Mechanics, 42(5), 754–759.
[CrossRef] [Google Scholar]
Riaz, A., Khan, S. U. D., Zeeshan, A., Khan, S. U., Hassan, M., & Muhammad, T. (2021). Thermal analysis of peristaltic flow of nanosized particles within a curved channel with second-order partial slip and porous medium. Journal of Thermal Analysis and Calorimetry, 143(3), 1997–2009.
[CrossRef] [Google Scholar]
Hayat, T., Javed, M., & Hendi, A. A. (2011). Peristaltic transport of viscous fluid in a curved channel with compliant walls. International Journal of Heat and Mass Transfer, 54(7–8), 1615–1621.
[CrossRef] [Google Scholar]
Hayat, T., Quratulain, Alsaadi, F., Rafiq, M., & Ahmad, B. (2017). On effects of thermal radiation and radial magnetic field for peristalsis of Sutterby liquid in a curved channel with wall properties. Chinese Journal of Physics, 55(5), 2005–2024.
[CrossRef] [Google Scholar]
Hayat, T., Farooq, S., Ahmad, B., & Alsaedi, A. (2016). Characteristics of convective heat transfer in the MHD peristalsis of Carreau fluid with Joule heating. AIP Advances, 6(4), 045302.
[CrossRef] [Google Scholar]
Shamshuddin, M. D., Khan, S. U., Bég, O. A., & Bég, T. A. (2020). Hall current, viscous and Joule heating effects on steady radiative 2-D magneto-power-law polymer dynamics from an exponentially stretching sheet with power-law slip velocity: A numerical study. Thermal Science and Engineering Progress, 20, 100732.
[CrossRef] [Google Scholar]
Hayat, T., Abbasi, F. M., Maryem, A., & Monaquel, S. (2014). Slip and Joule heating effects in mixed convection peristaltic transport of nanofluid with Soret and Dufour effects. Journal of Molecular Liquids, 194, 93–99.
[CrossRef] [Google Scholar]
Gireesha, B. J., Srinivasa, C. T., Shashikumar, N. S., Macha, M., Singh, J. K., & Mahanthesh, B. (2019). Entropy generation and heat transport analysis of Casson fluid flow with viscous and Joule heating in an inclined porous microchannel. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 233(4), 1173–1184.
[Google Scholar]
Sucharitha, G., Lakshminarayana, P., & Sandeep, N. (2017). Joule heating and wall flexibility effects on the peristaltic flow of magnetohydrodynamic nanofluid. International Journal of Mechanical Sciences, 131, 52–62.
[CrossRef] [Google Scholar]
Abbasi, A., Mabood, F., Farooq, W., & Khan, S. U. (2021). Radiation and Joule heating effects on electroosmosis-modulated peristaltic flow of Prandtl nanofluid via tapered channel. International Communications in Heat and Mass Transfer, 123, 105183.
[CrossRef] [Google Scholar]
Usman, M., Khan, M. I., Shah, F., Khan, S. U., Ghaffari, A., & Chu, Y. M. (2022). Heat and mass transfer analysis for bioconvective flow of Eyring Powell nanofluid over a Riga surface with nonlinear thermal features. Numerical Methods for Partial Differential Equations, 38(4), 777–793.
[CrossRef] [Google Scholar]
Kodi, R., Ravuri, M. R., Veeranna, V., Khan, M. I., Abdullaev, S., & Tamam, N. (2023). Hall current and thermal radiation effects of 3D rotating hybrid nanofluid reactive flow via stretched plate with internal heat absorption. Results in Physics, 53, 106915.
[CrossRef] [Google Scholar]
Rubbab, Q., Nazeer, M., Ahmad, F., Chu, Y. M., Khan, M. I., & Kadry, S. (2021). Numerical simulation of advection–diffusion equation with Caputo-Fabrizio time fractional derivative in cylindrical domains: Applications of pseudo-spectral collocation method. Alexandria Engineering Journal, 60(1), 1731–1738.
[CrossRef] [Google Scholar]
Rehman, M., Noreen, S., Haider, A., & Azam, H. (2015). Effect of heat sink/source on peristaltic flow of Jeffrey fluid through a symmetric channel. Alexandria Engineering Journal, 54(3), 733-743.
[CrossRef] [Google Scholar]
Li, Y. X., Alqsair, U. F., Ramesh, K., Khan, S. U., & Khan, M. I. (2021). Nonlinear heat source/sink and activation energy assessment in double diffusion flow of micropolar (non-Newtonian) nanofluid with convective conditions. Arabian Journal for Science and Engineering, 1-8.
[CrossRef] [Google Scholar]

Cite This Article

APA Style

Farooq, S., & Sana, A. (2025). Heat Transfer and Modified Darcy’s Principle in Peristaltic Motion with Hartmann Boundary Layer. ICCK Journal of Applied Mathematics, 1(1), 32–40. https://doi.org/10.62762/JAM.2025.463651

Article Metrics

Citations:

Google Scholar

Crossref

Scopus

Web of Science

Article Access Statistics:

PDF Downloads: 39

Publisher's Note

ICCK stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.

ICCK Journal of Applied Mathematics

ISSN: 3068-5656 (Online)

Email: [email protected]

Portico

All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/

Table of Content

1. Introduction

2. Formulation

3. The solution methodology

3.1 Asymptotic approximation for large magnetic field(𝐌)

3.2 The outer solution

3.3 The inner solutions

3.4 The higher order mode matching

4. Discussion

4.1 Velocity Profile

4.2 Temperature Profile

5. Concluding remarks

Google Scholar

Crossref

Scopus

Web of Science

We use cookies