Numerical Analysis of HBr-Cl2 Capacitive Coupled Plasma Using a Two-Dimensional Fluid Model

Iqra Shahzadi; Muhammad Waqar Ahmed

doi:10.62762/JAM.2025.440251

CiteScore

Impact Factor

Volume 1, Issue 1, ICCK Journal of Applied Mathematics

Volume 1, Issue 1, 2025

Submit Manuscript Edit a Special Issue

Table of Content

1. Introduction
2. Numerical Analysis
3. Chemical reactions
4. Results and Discussions
5. Conclusions

ICCK Journal of Applied Mathematics, Volume 1, Issue 1, 2025: 15-24

Open Access | Research Article | 21 June 2025

Numerical Analysis of HBr-Cl2 Capacitive Coupled Plasma Using a Two-Dimensional Fluid Model

Iqra Shahzadi 1

Muhammad Waqar Ahmed 1 *

1 Department of Physics, Riphah International University, Islamabad, Pakistan

* Corresponding Author: Muhammad Waqar Ahmed, [email protected]

DOI: 10.62762/JAM.2025.440251

Received: 18 April 2025, Accepted: 09 May 2025, Published: 21 June 2025

PDF (1.57 MB) Full-Text HTML XML

Article Metrics Cite This Article

Abstract

This research focuses on the computational analysis and numerical investigation of BrCl ion density within an HBr-Cl_2 capacitively coupled plasma system. A two-dimensional fluid simulation model was developed to examine the influence of varying the HBr: Cl_2 gas ratio on BrCl ion formation. The simulation framework incorporates fundamental plasma fluid equations, including the continuity equation, momentum conservation equations, and energy conservation equations, along with appropriate boundary conditions. The investigation specifically explored gas composition variations ranging from 10% Cl_2 and 90% HBr to 90% Cl_2 and 10% HBr, incremented in 20% steps. The radio frequency (RF) driving frequency was fixed at 13.56 MHz throughout the simulations. Results revealed a positive correlation between the Cl_2 concentration and the BrCl ion density; higher Cl_2 content led to increased BrCl ion production. Notably, elevated BrCl ion densities were observed near the electrode edges and at the electrode center. The generated two-dimensional and three-dimensional simulation data offer foundational insights for practical industrial applications, particularly in advanced semiconductor etching and deposition technologies.

Keywords

two-dimensional fluid simulation

BrCl ion density

numerical analysis

1. Introduction

In the semiconductor industry, plasma-based etching and deposition have become essential processes in microelectronic manufacturing, particularly through the use of halogen-based plasmas such as fluorine (F), chlorine (Cl), and bromine (Br). Compared to conventional wet chemical etching, dry etching is preferred due to its environmentally friendly nature and greater technical precision. Plasma etching offers numerous advantages over traditional methods, including enhanced anisotropy, better process control, and compatibility with advanced device geometries [1, 2, 3]. Both bromine and chlorine based plasma have their own merits and limitations for dry etch plasma applications, therefore it is necessary to discuss hidden aspects especially chemistry of bromine and chlorine based plasma [4]. The etching process strongly depends upon the type of gas especially type of halide gas used as the plasma generated species are important in dry etch applications. Many other parameters such as working pressure, gases flow rate, working temperature, type of plasma (RF, DC, Pulse DC or Microwave) strongly influence the etch process, like uniformity, proper selectivity, controlled etch rate and high performance of etching [5, 6]. The experimental process requires accurate and optimized parameters to achieve good results. In order to optimize correct parameters for the industrial application, numerical modeling and computational analysis of desired plasma is essential for defining the accurate parameters for performing experiments [7]. HBr-Cl₂ plasma is very useful in semiconductor industry especially for etching applications. In such plasma, the plasma chemistry is very important for etching applications therefore BrCl ions density is critical during the etching process in microelectronic manufacturing. After plasma confinement in capacitive coupled reactor, the BrCl ions formulates during some important chemical reactions like reaction of Cl radicals with HBr and reaction of bromine radicals with molecular chlorine, resulting in formation of BrCl and hydrogen and Cl. For these reactions electron impact ionization and ion impact dissociations both are responsible for the generation of BrCl ions. BrCl being polar diatomic molecule, with intermediate electronegativity difference makes it highly reactive [8, 9, 10, 11]. BrCl ions play a vital role in etching, being volatile they can remove material without effecting environment [12, 13]. Chlorine based plasmas have high etch rate as compared to bromine based plasma having less reactivity, but combination of BrCl can be dominant in etching process. Therefore composite of halide based plasma can be useful for etch applications [13]. The computational model designed in this research will be highly useful for determining the parameters for industrial applications.

2. Numerical Analysis

Fluid Simulation Model plays a vital role in this research. Different models and different numerical orders are used in this research to explain and evaluate fluid equations by different pattern of codes. Plasma is treated as a particular fluid in three-dimensional space, while species are influenced by the applied electric field. This model is based on density, flux, and mean energy of the species with respect to plasma. Equation is derivative of velocity distribution of Boltzmann equation. It offers us complete information comprising of all physical features like plasma chemistry, momentum, energy and electric field [14].

2.1 Reactor Geometry and Model

Our 2-Dimensional simulation comprised of geometry structure of CCP reactor which signify computational cell domain. The CCP reactor is operated by an RF power supply. CCP working principle is like a condenser in the circuit. It have two electrodes one is grounded other is connected thru power supply. CCP reactor contains gas mixture as input via nozzle while output contained etched materials at bottom of reactor. Three-dimensional having radius and Z are 15cm and 3cm with equally spaced $\Delta R$ and $\Delta Z$ respectively. Whole geometry is alienated into large numbers of grid cell. Each grid cell contain cells which is filled with dielectric material with certain voltages. For calculation of physical parameters like as density, field etc. electrostatic field is calculated at each grid cell and fluid equations are conforming to every cell discretized and solved iteratively. Equation of continuity is used for calculation of energy and number of density and momentum. Electron density and potentials are calculated at center of cell and at grid points respectively. Applications of this scheme are that plasma densities can be premeditated in front of the middle of adjacent plasma and dielectric surface. Boundary value deviousness of plasma densities is removed to half grid points to dielectric layer. Electrons are enhanced via field and flux of electrons are enormous to the wall. Which are origins of loss electrons to the wall of reactor. It indicate that formation of negative potential via creation of sheath region. This sheath is comprised of positive charges which decelerated striking electrons and speed up ions to reactor up to equalization both electrons and ions. This neutrality of bulk plasma contained charges are attained via positive plasma potential which permits the ions to speed up to reactor. Particles travels towards the reactor from higher density gradient towards lower density gradient. When energetic ions grasped at substrate and become penetrated and sputtered atoms in gaseous form from surface. This model demonstrated that spatial variation happened in actual rate of discharge and as well as identification numerous species and reactions occurred in reactor. Figure 1 illustrates the schematic of proposed CCP reactor.

Figure 1 CCP Computational geometry.

2.2 Numerical model

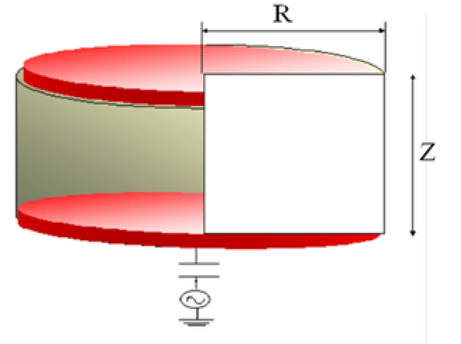
A plasma numerical model is a computational tool used to simulate and study the behavior of plasma under various conditions. It employs mathematical equations and algorithms to capture the complex interactions and dynamics of plasma particles, electric fields, and chemical reactions, providing valuable insights into plasma processes. Following are set of equations we used in our model [14].

2.2.1 Equation of Continuity

Based on observation, one of the postulate the idea is that mass is neither created nor destroyed. In other words, it is conserved. This is termed the Principle of Conservation of Mass. This principle is applied to a fixed volume of arbitrary shape in space that contains fluid. This volume is called "Control Volume." Fluid is permitted to enter or leave the control volume.

Rate of increase of mass of material within the control volume = Net rate at which mass enters the control volume.

By equation of continuity

\frac{\partial n_{e}}{\partial t}+\nabla\cdot(n_{e}v)=0

where as

\displaystyle\frac{\partial n_{e}}{\partial t}=\text{Rate of change of number % of density }

\displaystyle\text{with time}+\nabla\cdot(n_{e}v)=\text{Divergence of }n_{e}\times v

Here $n_{e}=n_{0}+n_{1}$ ( $n_{1}$ is neglected because it is so small).

Assuming that density of electrons ( $n_{e}$ ) is equal to density of ions ( $n_{i}$ ), so

\frac{\partial n_{1}}{\partial t}+\nabla\cdot(n_{0}v)=0

Differentiated with respect to $t$ :

\frac{\partial^{2}n_{1}}{\partial t^{2}}+n\cdot\nabla\frac{\partial v}{% \partial t}=0

As we know from single fluid equation of plasma:

\frac{\partial v}{\partial t}=\frac{e}{m}\nabla\varphi

Substituting of equation (4) in (3):

\frac{\partial^{2}n_{1}}{\partial t^{2}}+\frac{n_{0}e}{m}\nabla^{2}\varphi=0

\frac{\partial^{2}n_{1}}{\partial t^{2}}+\left(\frac{n_{0}e^{2}}{m\epsilon_{0}% }\right)n_{1}=0

2.2.2 Momentum Balance Equation

The Boltzmann equation is of fundamental importance in the kinetic theory of gases and plasmas. It expresses a mathematical description of the distribution function $f(r,v,t)$ of the particles at $(r,v)$ in the phase space and at time $t$ .

Boltzmann transformation equation is written as:

\frac{\partial f}{\partial t}+(v+\nabla)f+\frac{q}{m}(E+v\times B)\cdot\frac{% \partial f}{\partial v}=\left(\frac{df}{dt}\right)_{c}

Now multiplying the above equation with $m v$ and integrate all equation w.r.t to velocity space:

\begin{split}m\int\vec{v}\frac{\partial f}{\partial t}d^{3}v\nabla+&m\int v(v% \cdot\nabla)fd^{3}v\\ +\frac{q}{m}\int v(E+v\times B)\cdot&\frac{\partial f}{\partial v}d^{3}v\\ =&\int mv\left(\frac{df}{dt}\right)_{c}d^{3}v\end{split}

Taking equation (8) and solving all terms individually.

Now take 1st term of equation (8) and solve it:

m\int\vec{v}\frac{\partial f}{\partial t}d^{3}v=m\frac{\partial}{\partial t}% \int\vec{v}fd^{3}v

m\frac{\partial}{\partial t}\int\vec{v}fd^{3}v=m\frac{\partial}{\partial t}(n% \vec{u})

As knowing that

\int\vec{v}fd^{3}v=n\vec{u}

Now solve 2nd term of equation (8):

m\int\vec{v}(v\cdot\nabla)fd^{3}v=m\nabla\int\vec{v}\vec{v}fd^{3}v

m\nabla\int\vec{v}\vec{v}fd^{3}v=m\nabla\cdot(n\vec{v}\vec{v})

$\vec{v}\vec{v}$ = velocity of particles which is equal to average and thermal velocity.

According to definition of velocity equation (13) will be convert as:

m\nabla\cdot\left(n\vec{u}\vec{u}\right)+\nabla(mn\vec{w}\vec{w})

m\nabla\cdot\left(n\vec{u}\vec{u}\right)+\nabla p

m\left[u\nabla\cdot(nu)+n(u\cdot\nabla)u\right]

Now taking 3rd term of equation (8) evaluate it:

\begin{split}\int\frac{\partial}{\partial v}\cdot fv(E&+v\times B)d^{3}v=\int v% (E+v\times B)\frac{\partial f}{\partial v}d^{3}v\\ &+\int(E+v\times B)fd^{3}v\\ &+\int vf\frac{\partial}{\partial v}\cdot(E+v\times B)d^{3}v\end{split}

Volume integral is converged into surface integral when $v=\infty$ & $f=0$ . While 1st and 3rd term will be zero.

\begin{split}\oint_{s}^{v=0}fv(E&+v\times B)d^{3}v=\int v(E+V\times B)\frac{% \partial f}{\partial v}d^{3}v\\ &+\int(E+V\times B)fd^{3}v\\ &+\int\frac{\partial}{\partial v}\cdot\varphi(vf)(E+v\times B)fd^{3}v\end{split}

As we have

\int v(E+v\times B)\partial f/\partial vd^{3}v=-\int(E+v\times B)fd^{3}v

-\int(E+v\times B)fd^{3}v=-n(E+v\times B)

From the result of equation (8) we get that:

\int mv\left(\frac{dy}{dx}\right)_{\text{collision}}d^{3}v=P_{i,j}

Equation (21) is the representation of momentum change due to collision.

Whereas $P_{e,i}$ = change in momentum of electron due to ion

$P_{i,e}$ = Change in momentum of ion due to electron.

Now putting the values of equations (10), (16), (20) & (21) in equation (8):

\begin{split}m\frac{\partial}{\partial t}(nu)+&m\left[\mu\nabla\cdot(\mu\nabla% )+n(\mu\cdot\nabla)\mu\right]\\ &+\nabla p-qn(E+v\times B)=P_{i,j}\end{split}

As from equation of continuity:

\frac{\partial n}{\partial t}+\nabla\cdot(nu)=0

\nabla\cdot(nu)=-\partial n/\partial t

Putting the values in equation (22):

\begin{split}mn\frac{\partial u}{\partial t}+&mu\frac{\partial n}{\partial t}+% m\left[-u\frac{\partial n}{\partial t}+n(u\cdot\nabla)u\right]\\ &=nq(E+v\times B)-\nabla p+P_{i,j}\end{split}

mn\frac{\partial u}{\partial t}+mn(u\cdot\nabla)u=nq(E+v\times B)-\nabla p+P_{% i,j}

mn\left[\frac{\partial u}{\partial t}+(u\cdot\nabla)u\right]=nq(E+v\times B)-% \nabla p+p_{i,j}

Now represent equation (26) in the term of jth species:

\begin{split}m\frac{\partial}{\partial t}\left(n_{j}+u_{j}\right)+&\nabla\cdot% \left(m_{j}n_{j}u_{j}u_{j}\right)\\ &=eZ_{j}n_{j}E-\nabla P_{j}+mn_{j}v_{j}u_{j}\end{split}

$m\frac{\partial}{\partial t}\left(n_{j}+u_{j}\right)+\nabla\cdot\left(m_{j}n_{% j}u_{j}u_{j}\right)$ is the time dependent acceleration representation equation while $eZ_{j}n_{j}E-\nabla P_{j}+mn_{j}v_{j}u_{j}$ is representation of forces that are acting on the particles like pressure gradient, electric field and as well as particle collision.

Drift diffusion calculation of momentum equation assumed all the collisional process are dominant. Inertial effects of ions and time variation $\frac{\partial}{\partial t}(n_{j}u_{j})$ are neglected. So if time is changing slowly then temperature will have time to equilibrate with their term of ideal gas equation.

\nabla P_{j}=\nabla n_{j}K_{B}T

Now putting the values of equation (29) in (28):

\begin{split}m\frac{\partial}{\partial t}\left(n_{j}+u_{j}\right)+&\nabla\cdot% \left(m_{j}n_{j}u_{j}u_{j}\right)\\ &=eZ_{j}n_{j}E-\nabla n_{j}K_{B}T+mn_{j}v_{j}u_{j}\end{split}

m\frac{\partial}{\partial t}\left(n_{j}+u_{j}\right)+\nabla\cdot\left(m_{j}n_{% j}u_{j}u_{j}\right)=0

Putting in (30):

0=eZ_{j}n_{j}E-\nabla n_{j}K_{B}T+mn_{j}v_{j}u_{j}

Now write in terms of mobility and diffusion coefficient:

\Gamma_{j}=n_{j}\mu_{j}

n_{j}\mu_{j}=q_{j}\mu_{j}n_{j}E-D_{j}\nabla_{nj}

2.2.3 Energy Balance Equation

It is clear that the continuity equation provides the value of electron/ion density at the grid points and the Poisson equation offers the value of potential and electric field at the grid points. These Poisson and Continuity equations work together giving numerical values.

Balance and constitutive equations for the material domain part of a plasma fluid model for tokamaks. These equations are derivative of the Boltzmann equation, by the application of the classical kinetic theory approach. They can also be calculated and demonstrated in Hamiltonian form with the help of material products (balance equations for a moving material domain). The entropy balance and the Gibbs-Duhem equations acceptable us to calculate the irreversible entropy production (source) term. All these entropy production and transport occurrences have been recognized respectively with a R-field and Stokes-Dirac interconnection structures.

Energy is not properly transmitted in electron-neutral collision because masses are differ in the collision. So Boltzmann EEDF approximation is used at constant momentum transfer frequency and constant kinetic pressure.

\Gamma_{\epsilon}=-\mu_{\epsilon}E_{\epsilon}-\frac{\partial}{\partial z}(D_{% \epsilon}n_{\epsilon})

where as

\displaystyle\mu_{\epsilon}=\frac{5}{3}\mu_{e}

\displaystyle D_{\epsilon}=\frac{5}{3}D_{e}

Putting these values in equation (35):

\Gamma_{\epsilon}=\frac{5}{3}\Gamma\epsilon_{e}+q

(D and $\mu$ = mean energy of electron and grad of mean energy)

Whereas Q = heat flux.

Heat flux is directly varied to gradient of mean energy. Electron of random motion is

\epsilon=\frac{3}{2}K_{B}T

and

q=-\frac{5}{3}D_{e}n_{e}\nabla\epsilon

Now substituting the value of q in equation (36):

\Gamma_{\epsilon}=\frac{5}{3}\epsilon\Gamma_{e}-\frac{5}{3}D_{e}n_{e}\nabla\epsilon

As we have

\Gamma_{e}=D_{e}\nabla n_{e}-\mu_{e}n_{e}E

Substituting equation (40) in the equation (39):

\Gamma\epsilon=\frac{5}{3}\epsilon\left(D_{e}\nabla n_{e}-\mu_{e}n_{e}E\right)% -\frac{5}{3}D_{e}n_{e}\nabla\epsilon

\Gamma\epsilon=-\frac{5}{3}\epsilon\mu_{e}n_{e}E-\frac{5}{3}\epsilon D_{e}% \nabla n_{e}-\frac{5}{3}D_{e}n_{e}\nabla\epsilon

\Gamma\epsilon=-\frac{5}{3}\epsilon\mu_{e}n_{e}E-\frac{5}{3}D_{e}\nabla% \epsilon n_{e}

n_{\epsilon}=\epsilon n_{e}

Putting the values of equation (44) into (43):

\Gamma\epsilon=-\frac{5}{3}\mu_{e}n_{\epsilon}E-\frac{5}{3}D_{e}\nabla n\epsilon

As we know from equation of continuity:

\frac{\partial n_{\epsilon}}{\partial t}+\nabla\cdot\Gamma\epsilon=S\epsilon

S\epsilon=-e\Gamma\epsilon\cdot E-n_{e}\sum_{r}\epsilon_{r}n_{r}K_{r}

The above equation 1st term is representation of electron heat due to electric field and 2nd term is representative of collisional loss of electrons.

Whereas

$n_{r}$ = Density of target particles i-e r
$\epsilon_{r}$ = Collision of type r

2.2.4 Poisson's Equation

Poisson's equation is one of the essential parts of Electrostatics, where we would solve the equation to calculate electric potential from charge distribution. In layman's terms, we can use Poisson's Equation to define the static electricity of an object.

The Poisson equation is precarious to attain a self-consistent solution in plasma fluid simulations used for Hall Effect thrusters and streamer discharges. The Poisson solution performs as source term of the unsteady nonlinear flow equations. At first step, solving the 2D Poisson equation with zero Dirichlet boundary conditions by a deep neural network is examined via multiple-scale architectures, defined in terms of number of branches, depth and receptive field.

Poisson equation is base for modelling of semiconductor devices and as well as used in reactor for calculation of self-consistent electric field.

Applying relation of Maxwell's equations:

\nabla\cdot D=\rho

where

D=\epsilon E

D = Electric field displacement

$\epsilon$ = permittivity tensor

Putting the value of D in equation (48):

\nabla\cdot\epsilon E=\rho

Also knowing that gradient vector for electric field is:

E=-\nabla\vec{v}

Substituting the value of E in equation (50):

\nabla\cdot\left(\epsilon\nabla\vec{v}\right)=-\rho

\rho=q_{j}n_{j}

So putting the value of equation (53) in equation (52):

\nabla\cdot\left(\epsilon\nabla\vec{v}\right)=-q_{j}n_{j}

2.2.5 Boundary conditions

At lower and upper boundary perpendicular position of electric field exist as zero and also at both boundaries upper and lower net flux also zero due to boundary conditions. At left boundary electric field is also zero. Plasma dielectric interface possessing two boundaries conditions i-e the dielectric surface where charge accumulates and boundary in front of dielectric layer.

Equations (7), (28), (37), and (54) are complemented by boundary conditions like as for electric potential at the electrodes and walls of reactor.

v_{rf}=v_{0}\sin{(2\pi ft)}

$v_{0}=300v$ is the amplitude while frequency varies from 13.56MHz, 27.12MHz and 40.68MHz respectively.

$V_{\text{ground}}=0$ and $V_{\text{wall}}=0$

Boundary conditions for fluxes of electrons and ions are being calculated as:

\Gamma_{i}=\text{sign}\left(q_{i}\right)\mu_{i}n_{i}E+\frac{1}{4}n_{i}v_{th,i}

$v_{th,i}$ is symbolic representation of threshold velocity of charged species i.

For neutral species:

\Gamma_{i}^{in}=\frac{1}{4}n_{i}v_{th,j}\cdot\frac{\beta}{1-\frac{\beta}{2}}

where $\beta$ is the value of probability loss which is equivalant of sticking probability.

$\gamma=$ Sticking recombination probability of neutral species

And j = the surface recombination of neutral species

\Gamma_{i}^{out}=\sum_{j\neq i}\frac{\gamma_{i}}{\beta_{j}}\Gamma_{j}^{in}

3. Chemical reactions

In the process of producing BrCl ions in an HBr/Cl₂ capacitive coupled plasma, several chemical reactions can occur. Here is a list of some possible reactions that could contribute to the formation of BrCl ions:

HBr dissociation: HBr $\rightarrow$ H + Br
Cl₂ dissociation: Cl₂ $\rightarrow$ 2Cl
Cl dissociation: Cl $\rightarrow$ Cl* (excited state)
Cl* + HBr reaction: Cl* + HBr $\rightarrow$ H + BrCl
Br dissociation: Br $\rightarrow$ Br* (excited state)
Br* + Cl₂ reaction: Br* + Cl₂ $\rightarrow$ BrCl + Cl
Br* + HBr reaction: Br* + HBr $\rightarrow$ H + BrCl
Br + Cl₂ reaction: Br + Cl₂ $\rightarrow$ BrCl + Cl
Br + HBr reaction: Br + HBr $\rightarrow$ H + BrCl

Figure 2 BrCl density for 10% Cl₂ and 90%HBr.

Figure 3 BrCl density for 30% Cl₂ and 70%HBr.

4. Results and Discussions

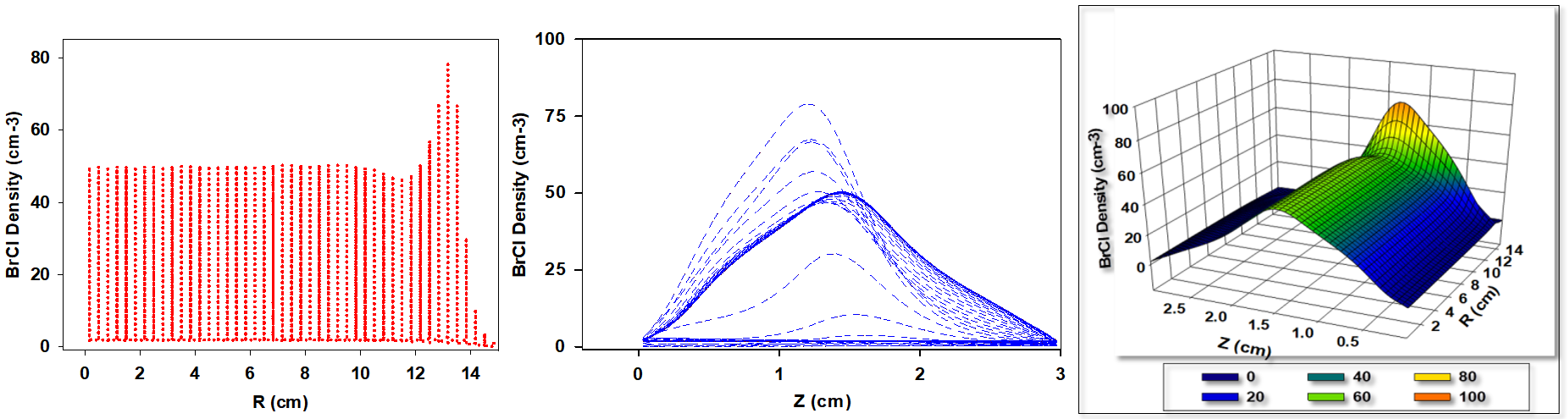
The fluid simulation of HBr - Cl₂ plasma was conducted to investigate the effect of varying gas ratios on BrCl ion density. This section presents the resulting trends in ion density and provides a detailed scientific explanation for the observed behavior and variations.

4.1 BrCl Ions Density for 10% Cl2 and 90% HBr

Figure 2 illustrates the computationally derived spatial distribution of BrCl⁺ ion densities for a gas mixture consisting of 10% Cl₂ and 90% HBr. Across the radial range from 0 to 11 cm, the BrCl⁺ ion density remains relatively uniform. However, a slight decline is observed at 12 cm, followed by a sharp increase, reaching a maximum density of approximately 80 cm^-3 at a radial distance of 14 cm. Along the axial direction (z-axis) between the electrodes, the BrCl⁺ ion density exhibits a bell-shaped profile, peaking at the midpoint between the electrodes. The data are visualized in a three-dimensional plot representing the initial BrCl⁺ ion densities under the specified gas composition. This behavior results from a combination of physical and chemical phenomena, including gas-phase reactions, diffusion, transport mechanisms, electric field effects, and the influence of the plasma sheath, as well as electron and ion energy distributions. At the electrode edges, the elevated concentration of reactive species leads to increased BrCl⁺ ion production. Additionally, enhanced diffusion and transport fluxes at these edges further contribute to the localized density increase. The characteristics of the plasma sheath—acting as a transitional boundary between the plasma bulk and the electrode surface—also play a significant role, depending on operating parameters such as gas pressure, applied voltage, and the nature of chemical reactions. Regions with elevated electron and ion energies promote ionization processes, thereby increasing the BrCl⁺ ion density.

4.2 BrCl Ions Density for 30% Cl and 70% HBr

Figure 4 BrCl density for 50% Cl₂ and 50%HBr.

Figure 5 BrCl density for 70% Cl₂ and 30%HBr.

Figure 6 BrCl density for 90% Cl₂ and 10%HBr.

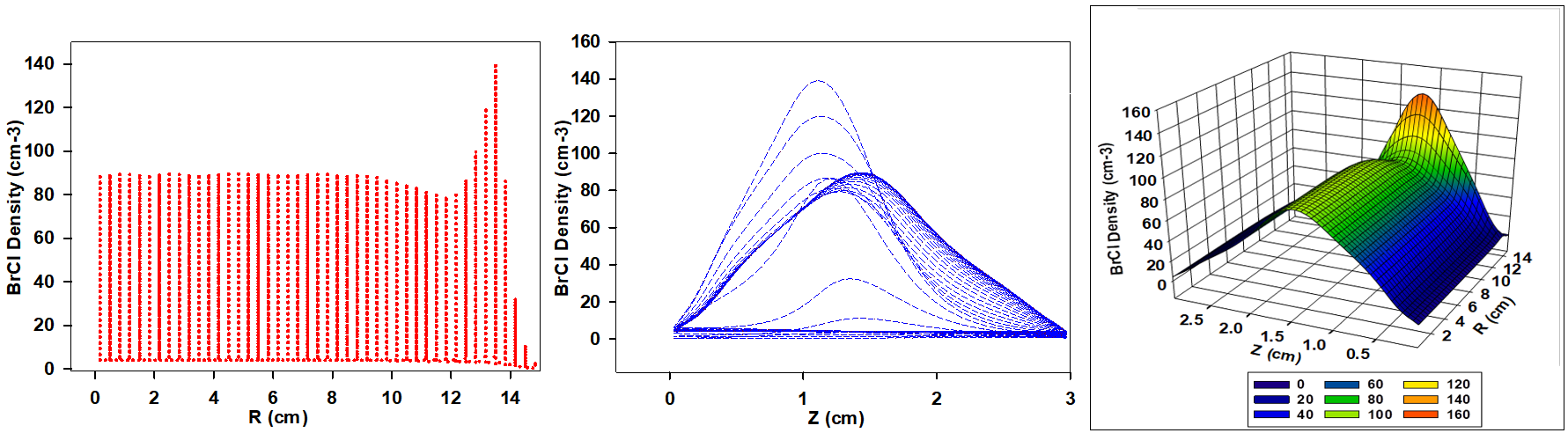
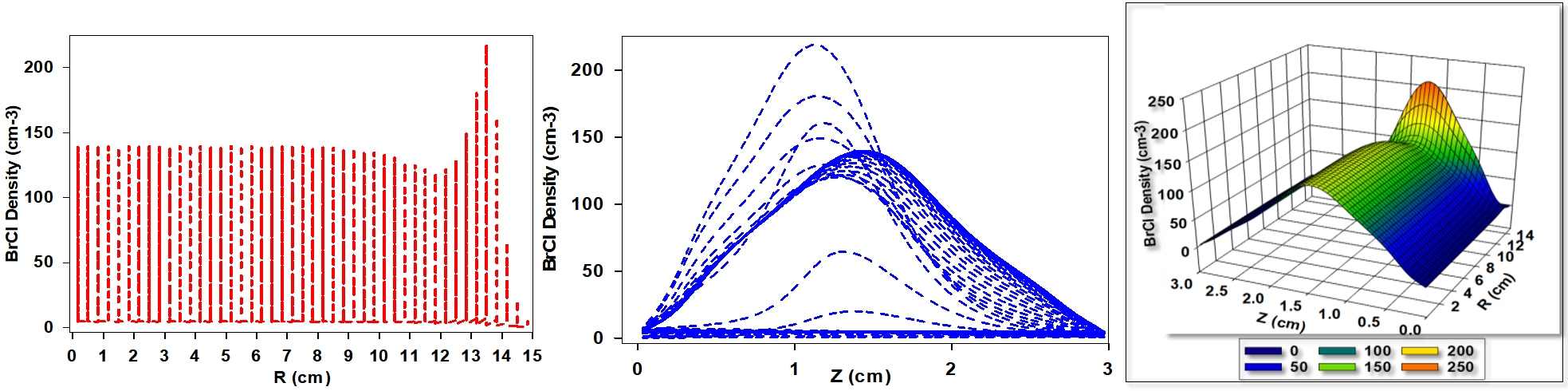
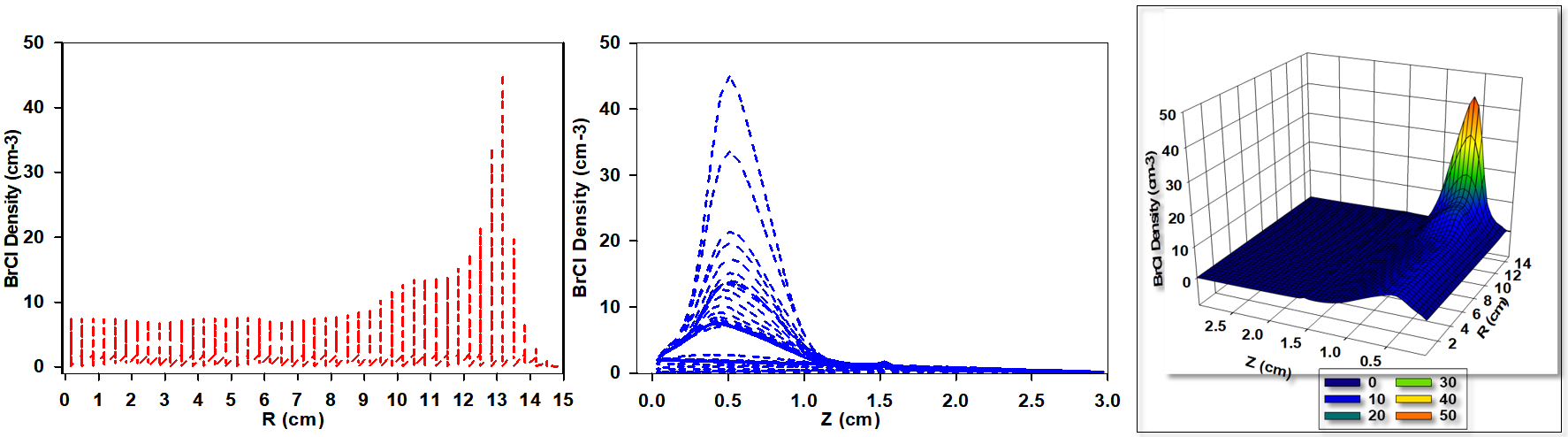
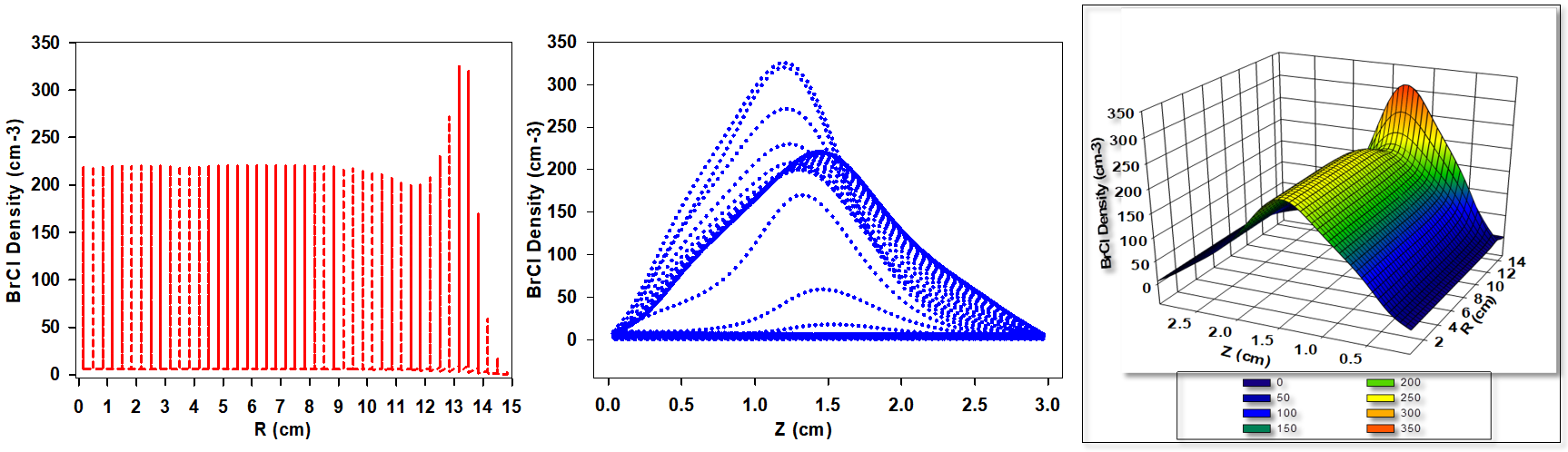
Figure 3 presents the simulated BrCl⁺ ion density distribution for a gas mixture composed of 30% Cl₂ and 70% HBr. While the qualitative behavior of ion density variation remains consistent with previous observations, a significant quantitative increase in BrCl⁺ ion density is evident. This enhancement is primarily attributed to the higher Cl₂ content, which intensifies chemical reaction rates, increases the dissociation of precursor molecules, and promotes overall ion generation. The elevated Cl₂ concentration facilitates more frequent and efficient reaction pathways, resulting in greater BrCl⁺ ion production. The increased Cl₂ flux enhances both ionization and dissociation processes, thereby contributing to the elevated BrCl⁺ ion density. Furthermore, the rise in chlorine content modifies key plasma parameters such as electron temperature, electron density, and the spatial distribution of the electric field. These altered plasma characteristics further influence the formation and transport of BrCl⁺ ions within the discharge region.

4.3 BrCl Ions Density for 50% Cl and 50% HBr

Figure 4 illustrates computationally calculated BrCl ions density for 50:50 of Cl₂ and HBr respectively in CCP. This balanced ratio provided interesting results with similar shapes of density variations but differing in quantity. Many factors collectively influence the variations of BrCl ions density including optimized conditions for the formation of BrCl ions at balance gas ratios. This balanced ratio increase collisional effects between Cl and HBr giving increase in concentration of BrCl ions density. At balanced ratio although both ionization and transport process also plays an important role in formation of BrCl ions. As compared to previous ratio the density of BrCl is lower at equal gas ratios.

4.4 BrCl Ions Density for 70% Cl2 and 30% HBr

Figure 5 illustrates the variation in BrCl⁺ ion density for a gas mixture containing 70% Cl₂ and 30% HBr, used in the simulation of a capacitively coupled plasma (CCP). While the overall trend in ion density behavior remains similar to previous cases, notable quantitative differences are observed. Specifically, the average BrCl⁺ ion density in this mixture is lower than that in the 30% Cl₂ / 70% HBr case but slightly higher than the mixture with equal proportions of Cl₂ and HBr.

A slight shift in the bell-shaped profile of BrCl⁺ ion density is evident, with peak densities now occurring closer to the electrode surfaces along the inter-electrode gap. The elevated Cl₂ ratio not only modifies the BrCl⁺ ion density distribution but also increases the frequency of collisions and enhances ionization processes. This is primarily due to chlorine's lower ionization energy compared to HBr, which facilitates a higher rate of BrCl⁺ ion generation. Despite these effects, the overall BrCl⁺ ion density remains lower than that observed for the 30% Cl₂ and 70% HBr gas composition.

4.5 BrCl Ions Density for 90% Cl2 and 10% HBr

Figure 6 illustrates the simulation results revealed a significant reduction in BrCl⁺ ion density at a gas composition of 90% Cl₂ and 10% HBr. Since HBr serves as a primary precursor in the formation of BrCl⁺ ions, its low concentration leads to a substantial decline in ion generation. This pronounced imbalance in the Cl₂-to-HBr ratio disrupts the plasma chemistry, resulting in an excess of chlorine-containing species and an overall suppression of BrCl⁺ ion production. Such a disproportionate gas mixture is unfavorable for applications that require stable or elevated BrCl⁺ ion densities, particularly in industrial plasma processes. Additionally, this imbalance alters key plasma parameters, including the electric field distribution and the ionization dynamics, further contributing to the observed reduction in BrCl⁺ ion density. Collectively, these factors explain the marked decrease in BrCl⁺ formation under these conditions.

5. Conclusions

A dominant role of gas ratio on densities of BrCl ions has been observed. The balance and ideal gas ratio has been defined in this conclusion. The results found that a mixture of 30% Cl₂ and 70% HBr is ideal for the highest BrCl ions density at the electrode center. The findings confirm that a variety of physical and chemical processes, including ionization, dissociation, and diffusion—contribute to the generation of BrCl ions within HBr-Cl₂ capacitive coupled plasma. Also the spatial distribution of BrCl ion density is not solely dependent on gas composition; the position within the electrode region, particularly at the edges and the center, also has a pronounced impact. Under the current numerical modeling conditions, a mixture of 30% Cl₂ and 70% HBr was found to yield the highest BrCl ion density at the electrode center. The research provides baseline data for ideal industrial applications.

Data Availability Statement

Data will be made available on request.

Funding

This work was supported without any funding.

Conflicts of Interest

The authors declare no conflicts of interest.

Ethical Approval and Consent to Participate

Not applicable.

References

Flamm, D. L. (1990). Mechanisms of silicon etching in fluorine-and chlorine-containing plasmas. Pure and Applied Chemistry, 62(9), 1709-1720.
[CrossRef] [Google Scholar]
Aldao, C. M., & Weaver, J. H. (2001). Halogen etching of Si via atomic-scale processes. Progress in surface science, 68(4-6), 189-230.
[CrossRef] [Google Scholar]
Cunge, G., Kogelschatz, M., & Sadeghi, N. (2004). Influence of reactor walls on plasma chemistry and on silicon etch product densities during silicon etching processes in halogen-based plasmas. Plasma Sources Science and Technology, 13(3), 522.
[CrossRef] [Google Scholar]
Ekinci, H., Kuryatkov, V. V., Mauch, D. L., Dickens, J. C., & Nikishin, S. A. (2014). Effect of BCl3 in chlorine-based plasma on etching 4H-SiC for photoconductive semiconductor switch applications. Journal of Vacuum Science & Technology B, 32(5).
[CrossRef] [Google Scholar]
Li, C., Yang, Y., Qu, R., Cao, X., Liu, G., Jin, X., ... & Liu, Y. (2024). Recent Advances in Plasma Etching for Micro and Nano Fabrications of Silicon-based Materials: A Review. Journal of Materials Chemistry C.
[CrossRef] [Google Scholar]
Donnelly, V. M., & Kornblit, A. (2013). Plasma etching: Yesterday, today, and tomorrow. Journal of Vacuum Science & Technology A, 31(5).
[CrossRef] [Google Scholar]
Kushner, M. J. (2009). Hybrid modelling of low temperature plasmas for fundamental investigations and equipment design. Journal of Physics D: Applied Physics, 42(19), 194013.
[CrossRef] [Google Scholar]
Efremov, A., Kim, Y., Lee, H. W., & Kwon, K. H. (2011). A comparative study of HBr-Ar and HBr-Cl 2 plasma chemistries for dry etch applications. Plasma Chemistry and Plasma Processing, 31, 259-271.
[CrossRef] [Google Scholar]
Bouchoule, S., Vallier, L., Patriarche, G., Chevolleau, T., & Cardinaud, C. (2012). Effect of Cl2-and HBr-based inductively coupled plasma etching on InP surface composition analyzed using in situ x-ray photoelectron spectroscopy. Journal of Vacuum Science & Technology A, 30(3).
[CrossRef] [Google Scholar]
Wagner, M. L., & Nine, R. (2013). The use of HBr in polysilicon etching. Gases & Instrumentation International, 7(4), 1-7. https://www.pall.com/content/dam/pall/microelectronics/literature-library/non-gated/HBr_Polysilicon.pdf
[Google Scholar]
Cunge, G., Inglebert, R. L., Joubert, O., Vallier, L., & Sadeghi, N. (2002). Ion flux composition in HBr/Cl 2/O 2 and HBr/Cl 2/O 2/CF 4 chemistries during silicon etching in industrial high-density plasmas. Journal of Vacuum Science & Technology B: Microelectronics and Nanometer Structures Processing, Measurement, and Phenomena, 20(5), 2137-2148.
[CrossRef] [Google Scholar]
Ono, K., Ohta, H., & Eriguchi, K. (2010). Plasma–surface interactions for advanced plasma etching processes in nanoscale ULSI device fabrication: A numerical and experimental study. Thin Solid Films, 518(13), 3461-3468.
[CrossRef] [Google Scholar]
Majeed, M., Gul, B., & Zia, G. (2020). Numerical investigation of the effect of variation of gas mixture ratio on density distribution of etchant species (Br, Br+, Cl, Cl+, and H) in HBr/Cl 2/Ar plasma discharge. The European Physical Journal D, 74, 1-10.
[CrossRef] [Google Scholar]
Gul, B., Ahmad, I., & Zia, G. (2016). Numerical study of capacitive coupled HBr/Cl2 plasma discharge for dry etch applications. Physics of Plasmas, 23(9).
[CrossRef] [Google Scholar]

Cite This Article

APA Style

Shahzadi, I., & Ahmed, M. W. (2025). Numerical Analysis of HBr-Cl2 Capacitive Coupled Plasma Using a Two-Dimensional Fluid Model. ICCK Journal of Applied Mathematics, 1(1), 15–24. https://doi.org/10.62762/JAM.2025.440251

Article Metrics

Citations:

Google Scholar

Crossref

Scopus

Web of Science

Article Access Statistics:

PDF Downloads: 48

Publisher's Note

ICCK stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.

ICCK Journal of Applied Mathematics

ISSN: 3068-5656 (Online)

Email: [email protected]

Portico

All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/