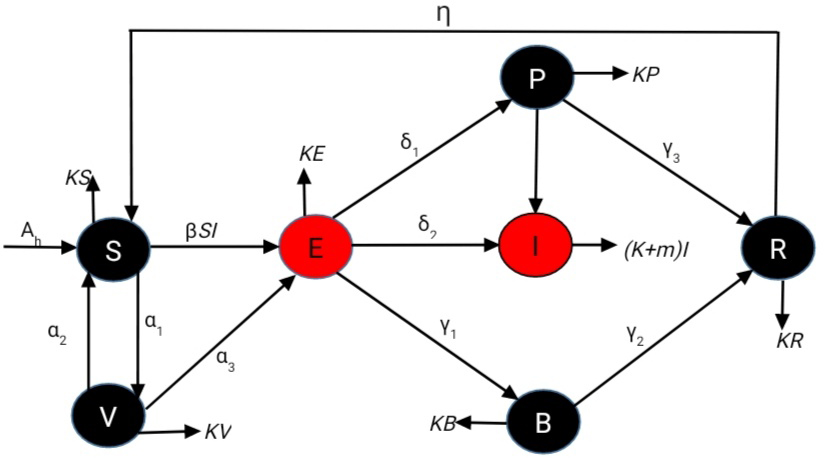
Rabies remains a serious public health concern, as dog bites account for the majority of human cases. In this study, we develop a comprehensive mathematical model to investigate the dynamics of rabies transmission by incorporating two key intervention strategies: an asymptotic class (\(P\)) and a booster vaccination class (\(B\)). The basic reproduction number (\(R_0\)) is derived as a threshold parameter that governs whether the disease spreads or dies out, based on a system of nonlinear differential equations. A sensitivity analysis of \(R_0\) is conducted to identify the most influential parameters affecting disease transmission. The results indicate that the transmission rate (\(\beta\))... More >

Despite extensive study of max--min problems, convergence analysis for the challenging nonconvex--nonconcave setting remains limited. This paper addresses the convergence analysis of nonconvex--nonconcave max--min problems. A novel analytical framework is developed by employing carefully constructed auxiliary functions and leveraging two-sided Polyak--Łojasiewicz (PL) and Quadratic Growth (QG) conditions to characterize the convergence behavior. Under these conditions, it is shown that the Stochastic Alternating Gradient Descent Ascent (SAGDA) algorithm achieves a convergence rate of $\mathcal{O}\left(1/K\right)$, where $K$ denotes the number of iterations. Notably, this result matches conv... More >

This study investigates two transitions in cosmology: radiation-matter and matter-dark energy. For each transition, a parameter $\chi$ is employed, representing the ratio of the two energy densities involved in the relevant transition. The focus on the second transition is motivated by the need to understand an accelerating universe. In examining potential cosmic acceleration due to dynamic dark energy, a dynamical equation of state for dark energy is considered in terms of the ratio $\chi$ and the deceleration parameter $q$. The resulting system of equations is analyzed by varying parameters to investigate their influence on the evolution of the universe. To achieve cosmic acceleration, the... More >

The objective of the research was to perform computer simulation of diffusion in a mixture of ideal gases considering the dependence of the diffusion coefficient on the entropy of mixing according to the proposed mathematical model. Computer simulation was carried out in one-dimensional and two-dimensional settings using finite element method and Python programming language with the use of NumPy and SciPy libraries. The obtained results show that the proposed mathematical model of diffusion in a mixture of ideal gases could be used to solve computer simulation tasks of gas diffusion satisfying the principle of mass conservation, because the entropy is considered via the chemical potential. More >

Binary functions have a wide range of applications in the fields of machine learning, statistical learning, and so on. In this paper, we investigate the exponential inequalities for the independent $V$-statistics of binary affine functions and obtain a universal inequality for $V$-statistics. Due to the typical characteristics of this kind of binary function, including symmetry and affinity, this work has great practical significance. Finally, we derive the corresponding inequalities in the context of specific similarity learning. More >