Computer Simulation of Diffusion in a Mixture of Ideal Gases Considering the Dependence of the Diffusion Coefficient on the Entropy of Mixing Using Finite Element Method

Pavel Shalkevich; Nikita Tsvikevich

doi:10.62762/JNSPM.2025.504999

CiteScore

Impact Factor

Volume 1, Issue 2, Journal of Numerical Simulations in Physics and Mathematics

Volume 1, Issue 2, 2025

Submit Manuscript Edit a Special Issue

Article QR Code

Scan the QR code for reading

Popular articles

Case Studies on Integrating Artificial Intelligence in Finance to Transform Decision Making and Risk Management for Enhanced Financial Outcomes Research on A Ship Trajectory Classification Method Based on Deep Learning Bridging Modalities: A Survey of Cross-Modal Image-Text Retrieval Enhancing Fake News Detection with a Hybrid NLP-Machine Learning Framework Reinforcement Learning for Prompt Optimization in Language Models: A Comprehensive Survey of Methods, Representations, and Evaluation Challenges Plant Disease Detection Using Deep Learning Techniques A Mimic Fusion Algorithm for Dual Channel Video Based on Possibility Distribution Synthesis Theory YOLOv7-Bw: A Dense Small Object Efficient Detector Based on Remote Sensing Image Deep Prediction Network Based on Covariance Intersection Fusion for Sensor Data Analyzing the Translation and Impact of Popular Science Literature in China: A Case Study Approach

Journal of Numerical Simulations in Physics and Mathematics, Volume 1, Issue 2, 2025: 60-66

Open Access | Research Article | 29 October 2024

Computer Simulation of Diffusion in a Mixture of Ideal Gases Considering the Dependence of the Diffusion Coefficient on the Entropy of Mixing Using Finite Element Method

Pavel Shalkevich 1 *

Nikita Tsvikevich 1

1 Chair of Information Technologies in Ecology and Medicine, International Sakharov Environmental Institute of Belarusian State University, Minsk 220070, Belarus

* Corresponding Author: Pavel Shalkevich, [email protected]

DOI: 10.62762/JNSPM.2025.504999

Received: 29 September 2025, Accepted: 12 October 2025, Published: 29 October 2024

PDF (1.83 MB)

Article Metrics Cite This Article

Abstract

The objective of the research was to perform computer simulation of diffusion in a mixture of ideal gases considering the dependence of the diffusion coefficient on the entropy of mixing according to the proposed mathematical model. Computer simulation was carried out in one-dimensional and two-dimensional settings using finite element method and Python programming language with the use of NumPy and SciPy libraries. The obtained results show that the proposed mathematical model of diffusion in a mixture of ideal gases could be used to solve computer simulation tasks of gas diffusion satisfying the principle of mass conservation, because the entropy is considered via the chemical potential.

Graphical Abstract

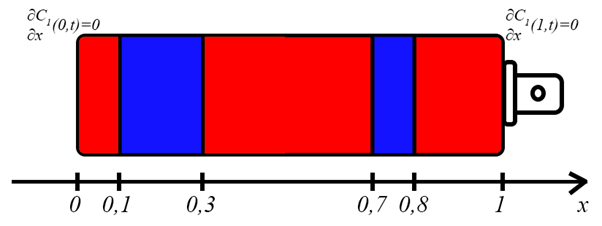
Computer Simulation of Diffusion in a Mixture of Ideal Gases Considering the Dependence of the Diffusion Coefficient on the Entropy of Mixing Using Finite Element Method

Keywords

computer modeling

mathematical modeling

gas diffusion

entropy of gas mixing

chemical potential

finite element method

numerical methods

Data Availability Statement

Data will be made available on request.

Funding

This work was supported without any funding.

Conflicts of Interest

The authors declare no conflicts of interest.

Ethical Approval and Consent to Participate

Not applicable.

References

Monteith, J., & Unsworth, M. (2013). Principles of environmental physics: plants, animals, and the atmosphere. Academic press.
[Google Scholar]
Plawsky, J. L. (2020). Transport phenomena fundamentals. CRC press.
[Google Scholar]
West, J. B. (2012). Respiratory physiology: the essentials. Lippincott Williams & Wilkins.
[Google Scholar]
Weibel, E. R. (1984). The pathway for oxygen: structure and function in the mammalian respiratory system. Harvard University Press.
[Google Scholar]
Vera, L., Campos Arias, D., Muylle, S., Stergiopulos, N., Segers, P., & van Loon, G. (2019). A 1D computer model of the arterial circulation in horses: An important resource for studying global interactions between heart and vessels under normal and pathological conditions. PloS one, 14(8), e0221425.
[CrossRef] [Google Scholar]
Gibbs, J. W. (1928). The Collected Works of J. Willard Gibbs...: Thermodynamics (Vol. 1). Longmans, Green and Company.
[Google Scholar]
Bose, S. N. (2009). Thermal Equilibrium in the Radiation Field in the. Satyendra Nath Bose: His Life and Times: Selected Works (with Commentary), 40.
[Google Scholar]
Elizarova, T. G., Khokhlov, A. A., & Montero, S. (2007). Numerical simulation of shock wave structure in nitrogen. Physics of Fluids, 19(6). [
[CrossRef] [Google Scholar]
Rój, E., & Dmoch, M. (2007). CFD study of gas mixing efficiency and comparisons with experimental data. In Computer Aided Chemical Engineering (Vol. 24, pp. 509-514). Elsevier. [
[CrossRef] [Google Scholar]
Fei, W. A. N. G., & Ziqing, P. A. N. (2016). Numerical simulation of chemical potential dominated fracturing fluid flowback in hydraulically fractured shale gas reservoirs. Petroleum Exploration and Development, 43(6), 1060-1066. [
[CrossRef] [Google Scholar]
Klevs, M., Zageris, G., Ziemelis, A. A., Dzelme, V., Geza, V., & Jakovics, A. (2023). Numerical insights into gas mixing system design for energy conversion processes. Latvian Journal of Physics and Technical Sciences, 60(s6), 44-59. [
[CrossRef] [Google Scholar]
Sato, N. (2004). Chemical energy and exergy: an introduction to chemical thermodynamics for engineers. Elsevier.
[Google Scholar]
Gjennestad, M. A., & Wilhelmsen, Ø. (2024). Thermodynamically consistent modeling of gas flow and adsorption in porous media. International Journal of Heat and Mass Transfer, 226, 125462. [
[CrossRef] [Google Scholar]
Shalkevich, P. K. (2021). Computer prediction of the spatial distribution of the Cs-137 concentration in soil. Doklady of the National Academy of Sciences of Belarus, 65(2), 139-145. [
[CrossRef] [Google Scholar]

Cite This Article

APA Style

Shalkevich, P., & Tsvikevich, N. (2025). Computer Simulation of Diffusion in a Mixture of Ideal Gases Considering the Dependence of the Diffusion Coefficient on the Entropy of Mixing Using Finite Element Method. Journal of Numerical Simulations in Physics and Mathematics, 1(2), 60–66. https://doi.org/10.62762/JNSPM.2025.504999

Article Metrics

Citations:

Google Scholar

Crossref

Scopus

Web of Science

Article Access Statistics:

PDF Downloads: 6

Publisher's Note

ICCK stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and Permissions

Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.

Journal of Numerical Simulations in Physics and Mathematics

ISSN: 3068-9082 (Online) | ISSN: 3068-9074 (Print)

Email: [email protected]

Portico

All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/

Google Scholar

Crossref

Scopus

Web of Science

We use cookies