Submit Manuscript
Edit a Special Issue
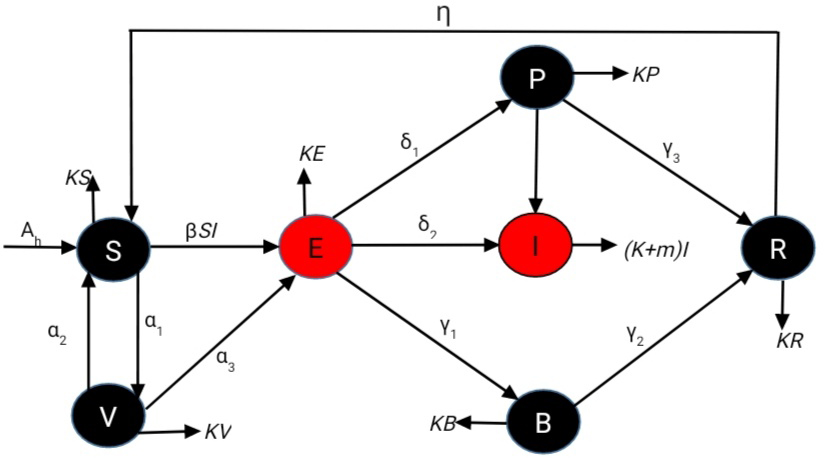
TY - JOUR AU - Ullah, Hanif AU - Ali, Amjid AU - Younas, Hazrat PY - 2025 DA - 2025/12/11 TI - Modeling the Impact of Vaccination and Post-Treatment on Rabies Transmission JO - Journal of Numerical Simulations in Physics and Mathematics T2 - Journal of Numerical Simulations in Physics and Mathematics JF - Journal of Numerical Simulations in Physics and Mathematics VL - 1 IS - 2 SP - 84 EP - 97 DO - 10.62762/JNSPM.2025.826101 UR - https://www.icck.org/article/abs/JNSPM.2025.826101 KW - rabies KW - mathematical model KW - stability KW - bifurcation KW - rabies model AB - Rabies remains a serious public health concern, as dog bites account for the majority of human cases. In this study, we develop a comprehensive mathematical model to investigate the dynamics of rabies transmission by incorporating two key intervention strategies: an asymptotic class (\(P\)) and a booster vaccination class (\(B\)). The basic reproduction number (\(R_0\)) is derived as a threshold parameter that governs whether the disease spreads or dies out, based on a system of nonlinear differential equations. A sensitivity analysis of \(R_0\) is conducted to identify the most influential parameters affecting disease transmission. The results indicate that the transmission rate (\(\beta\)) has a significant impact on \(R_0\), emphasizing the importance of reducing contact between susceptible and infected populations. Stability analysis of both the disease-free and endemic equilibria reveals that the disease can be eradicated when \(R_0 < 1\), whereas it persists when \(R_0 > 1\). Numerical simulations, performed using the classical Runge–Kutta method, illustrate the comparative effects of vaccination and treatment interventions. The results demonstrate that the inclusion of the booster vaccination class (\(B\)) substantially reduces the number of infected individuals compared to the scenario without vaccination. Moreover, the therapeutic class (\(P\)) further accelerates recovery and alleviates the overall disease burden. Analysis of varying transmission rates (\(\beta\)) shows that higher values lead to a rapid rise in infection levels, underscoring the necessity for effective intervention strategies in high-contact environments. Overall, the model highlights that integrating booster vaccination and treatment measures within rabies control programs can significantly decrease disease prevalence. The findings of this study provide valuable insights for public health authorities aiming to design efficient strategies for the control and eventual eradication of rabies. SN - 3068-9082 PB - Institute of Central Computation and Knowledge LA - English ER -
@article{Ullah2025Modeling,
author = {Hanif Ullah and Amjid Ali and Hazrat Younas},
title = {Modeling the Impact of Vaccination and Post-Treatment on Rabies Transmission},
journal = {Journal of Numerical Simulations in Physics and Mathematics},
year = {2025},
volume = {1},
number = {2},
pages = {84-97},
doi = {10.62762/JNSPM.2025.826101},
url = {https://www.icck.org/article/abs/JNSPM.2025.826101},
abstract = {Rabies remains a serious public health concern, as dog bites account for the majority of human cases. In this study, we develop a comprehensive mathematical model to investigate the dynamics of rabies transmission by incorporating two key intervention strategies: an asymptotic class (\(P\)) and a booster vaccination class (\(B\)). The basic reproduction number (\(R\_0\)) is derived as a threshold parameter that governs whether the disease spreads or dies out, based on a system of nonlinear differential equations. A sensitivity analysis of \(R\_0\) is conducted to identify the most influential parameters affecting disease transmission. The results indicate that the transmission rate (\(\beta\)) has a significant impact on \(R\_0\), emphasizing the importance of reducing contact between susceptible and infected populations. Stability analysis of both the disease-free and endemic equilibria reveals that the disease can be eradicated when \(R\_0 < 1\), whereas it persists when \(R\_0 > 1\). Numerical simulations, performed using the classical Runge–Kutta method, illustrate the comparative effects of vaccination and treatment interventions. The results demonstrate that the inclusion of the booster vaccination class (\(B\)) substantially reduces the number of infected individuals compared to the scenario without vaccination. Moreover, the therapeutic class (\(P\)) further accelerates recovery and alleviates the overall disease burden. Analysis of varying transmission rates (\(\beta\)) shows that higher values lead to a rapid rise in infection levels, underscoring the necessity for effective intervention strategies in high-contact environments. Overall, the model highlights that integrating booster vaccination and treatment measures within rabies control programs can significantly decrease disease prevalence. The findings of this study provide valuable insights for public health authorities aiming to design efficient strategies for the control and eventual eradication of rabies.},
keywords = {rabies, mathematical model, stability, bifurcation, rabies model},
issn = {3068-9082},
publisher = {Institute of Central Computation and Knowledge}
}
Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. 
Journal of Numerical Simulations in Physics and Mathematics
ISSN: 3068-9082 (Online) | ISSN: 3068-9074 (Print)
Email: [email protected]
Portico
All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/