On the Convergence of Nonconcave-Nonconvex Max-Min Optimization Problem

Xuelin Zhang

doi:10.62762/JNSPM.2025.112121

CiteScore

Impact Factor

Volume 1, Issue 2, Journal of Numerical Simulations in Physics and Mathematics

Volume 1, Issue 2, 2025

Submit Manuscript Edit a Special Issue

Article QR Code

Scan the QR code for reading

Popular articles

Case Studies on Integrating Artificial Intelligence in Finance to Transform Decision Making and Risk Management for Enhanced Financial Outcomes Reinforcement Learning for Prompt Optimization in Language Models: A Comprehensive Survey of Methods, Representations, and Evaluation Challenges AI and the Future of Education: Advancing Personalized Learning and Intelligent Tutoring Systems Plant Disease Detection Using Deep Learning Techniques Modeling Brain Functional Networks Using Graph Neural Networks: A Review and Clinical Application Bridging Modalities: A Survey of Cross-Modal Image-Text Retrieval Research on A Ship Trajectory Classification Method Based on Deep Learning Acrylamide in Food: Sources and Prevention Enhancing Fake News Detection with a Hybrid NLP-Machine Learning Framework Analyzing the Translation and Impact of Popular Science Literature in China: A Case Study Approach

Journal of Numerical Simulations in Physics and Mathematics, Volume 1, Issue 2, 2025: 76-83

Open Access | Research Article | 08 December 2025

On the Convergence of Nonconcave-Nonconvex Max-Min Optimization Problem

Xuelin Zhang 1 *

1 College of Informatics, Huazhong Agricultural University, Wuhan 430070, China

* Corresponding Author: Xuelin Zhang, [email protected]

DOI: 10.62762/JNSPM.2025.112121

Received: 14 October 2025, Accepted: 18 October 2025, Published: 08 December 2025

PDF (2.25 MB)

Article Metrics Cite This Article

Abstract

Despite extensive study of max--min problems, convergence analysis for the challenging nonconvex--nonconcave setting remains limited. This paper addresses the convergence analysis of nonconvex--nonconcave max--min problems. A novel analytical framework is developed by employing carefully constructed auxiliary functions and leveraging two-sided Polyak--Łojasiewicz (PL) and Quadratic Growth (QG) conditions to characterize the convergence behavior. Under these conditions, it is shown that the Stochastic Alternating Gradient Descent Ascent (SAGDA) algorithm achieves a convergence rate of $\mathcal{O}\left(1/K\right)$, where $K$ denotes the number of iterations. Notably, this result matches convergence rates typically obtained in (weakly) convex--concave minimax settings while requiring significantly milder geometric assumptions. The theoretical results are further validated through empirical experiments on realistic examples.

Graphical Abstract

Keywords

max-min optimization

convergence guarantee

nonconvex-nonconcave problems

two-sided polyak-lojasiewicz

quadratic growth

Data Availability Statement

Data will be made available on request.

Funding

This work was supported without any funding.

Conflicts of Interest

The author declares no conflicts of interest.

Ethical Approval and Consent to Participate

Not applicable.

References

Donoho, D. L., & Johnstone, I. M. (1996). Neo-classical minimax problems, thresholding and adaptive function estimation. Bernoulli, 2(1), 39-62.
[CrossRef] [Google Scholar]
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., ... & Bengio, Y. (2020). Generative adversarial networks. Communications of the ACM, 63(11), 139-144.
[CrossRef] [Google Scholar]
Gulrajani, I., Ahmed, F., Arjovsky, M., Dumoulin, V., & Courville, A. C. (2017). Improved training of wasserstein gans. Advances in neural information processing systems, 30.
[Google Scholar]
Heusel, M., Ramsauer, H., Unterthiner, T., Nessler, B., & Hochreiter, S. (2017). Gans trained by a two time-scale update rule converge to a local nash equilibrium. Advances in neural information processing systems, 30.
[Google Scholar]
Karimi, H., Nutini, J., & Schmidt, M. (2016, September). Linear convergence of gradient and proximal-gradient methods under the polyak-łojasiewicz condition. In Joint European conference on machine learning and knowledge discovery in databases (pp. 795-811). Cham: Springer International Publishing.
[CrossRef] [Google Scholar]
Lin, T., Jin, C., & Jordan, M. I. (2020, July). Near-optimal algorithms for minimax optimization. In Conference on learning theory (pp. 2738-2779). PMLR.
[Google Scholar]
Lin, T., Jin, C., & Jordan, M. I. (2025). Two-timescale gradient descent ascent algorithms for nonconvex minimax optimization. Journal of Machine Learning Research, 26(11), 1-45.
[Google Scholar]
Liu, M., Rafique, H., Lin, Q., & Yang, T. (2021). First-order convergence theory for weakly-convex-weakly-concave min-max problems. Journal of Machine Learning Research, 22(169), 1–34.
[Google Scholar]
Nouiehed, M., Sanjabi, M., Huang, T., Lee, J. D., & Razaviyayn, M. (2019). Solving a class of non-convex min-max games using iterative first order methods. Advances in Neural Information Processing Systems, 32.
[Google Scholar]
Palaniappan, B., & Bach, F. (2016). Stochastic variance reduction methods for saddle-point problems. Advances in Neural Information Processing Systems, 29.
[Google Scholar]
Razaviyayn, M., Huang, T., Lu, S., Nouiehed, M., Sanjabi, M., & Hong, M. (2020). Nonconvex min-max optimization: Applications, challenges, and recent theoretical advances. IEEE Signal Processing Magazine, 37(5), 55-66.
[CrossRef] [Google Scholar]
Sion, M. (1958). On general minimax theorems. Pacific Journal of Mathematics, 8(1), 171–176.
[CrossRef] [Google Scholar]
Yang, J., Kiyavash, N., & He, N. (2020). Global convergence and variance reduction for a class of nonconvex-nonconcave minimax problems. Advances in Neural Information Processing Systems, 33, 1153–1165.
[Google Scholar]
Yang, S., Li, X., & Lan, G. (2025). Data-driven minimax optimization with expectation constraints. Operations Research, 73(3), 1345–1365.
[CrossRef] [Google Scholar]
Zhang, X., Chen, H., Gu, B., Gong, T., & Zheng, F. (2024). Fine-grained analysis of stability and generalization for stochastic bilevel optimization. In Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence (pp. 5508–5516).
[CrossRef] [Google Scholar]
Jin, C., Netrapalli, P., & Jordan, M. (2020, November). What is local optimality in nonconvex-nonconcave minimax optimization?. In International conference on machine learning (pp. 4880-4889). PMLR.
[Google Scholar]
Barrett, D. G., & Dherin, B. (2020). Implicit gradient regularization. arXiv preprint arXiv:2009.11162.
[Google Scholar]

Cite This Article

APA Style

Zhang, X. (2025). On the Convergence of Nonconcave-Nonconvex Max-Min Optimization Problem. Journal of Numerical Simulations in Physics and Mathematics, 1(2), 76–83. https://doi.org/10.62762/JNSPM.2025.112121

Export Citation

RIS Format

Compatible with EndNote, Zotero, Mendeley, and other reference managers

RIS format data for reference managers

TY  - JOUR
AU  - Zhang, Xuelin
PY  - 2025
DA  - 2025/12/08
TI  - On the Convergence of Nonconcave-Nonconvex Max-Min Optimization Problem
JO  - Journal of Numerical Simulations in Physics and Mathematics
T2  - Journal of Numerical Simulations in Physics and Mathematics
JF  - Journal of Numerical Simulations in Physics and Mathematics
VL  - 1
IS  - 2
SP  - 76
EP  - 83
DO  - 10.62762/JNSPM.2025.112121
UR  - https://www.icck.org/article/abs/JNSPM.2025.112121
KW  - max-min optimization
KW  - convergence guarantee
KW  - nonconvex-nonconcave problems
KW  - two-sided polyak-lojasiewicz
KW  - quadratic growth
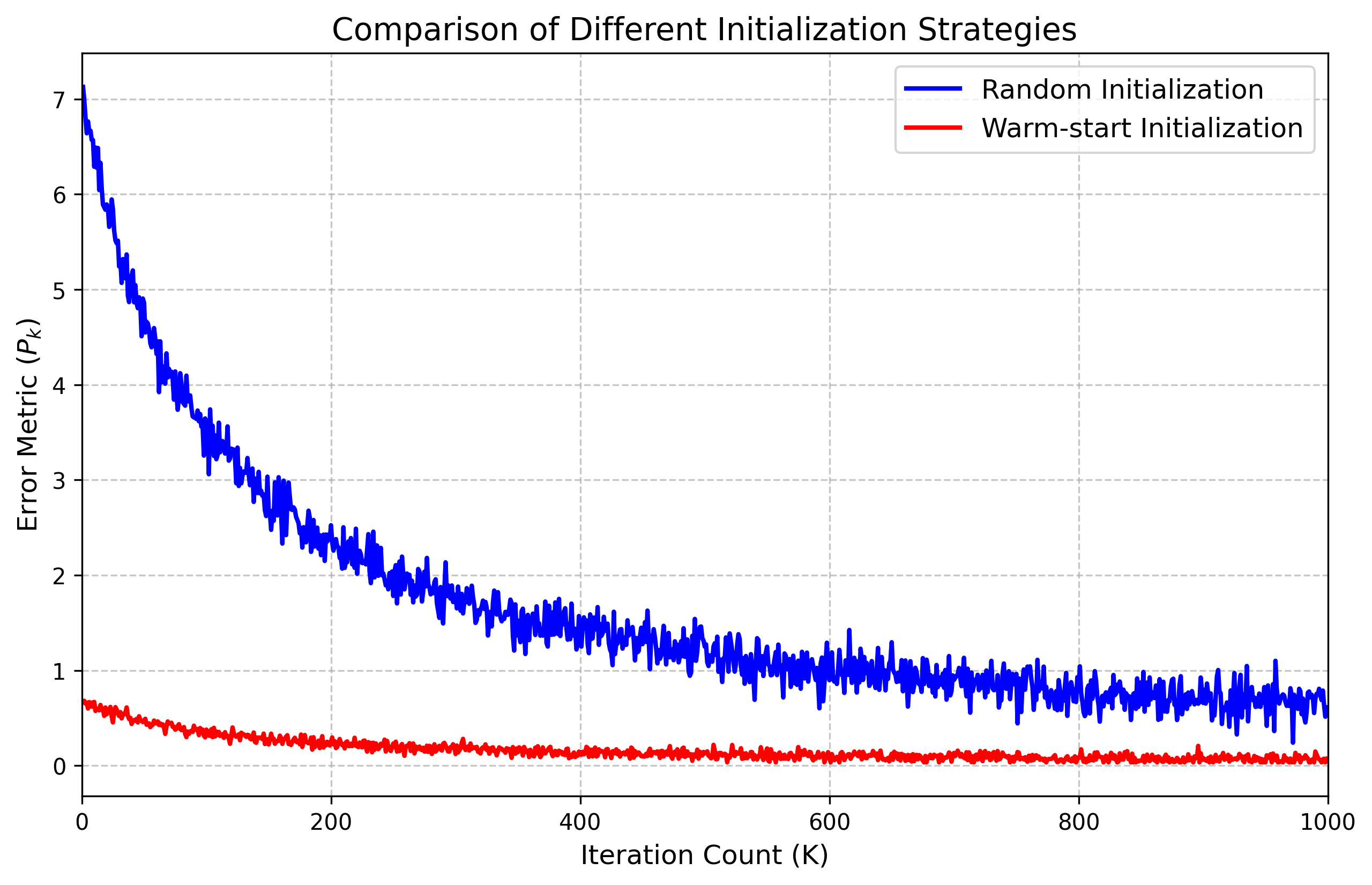
AB  - Despite extensive study of max--min problems, convergence analysis for the challenging nonconvex--nonconcave setting remains limited. This paper addresses the convergence analysis of nonconvex--nonconcave max--min problems. A novel analytical framework is developed by employing carefully constructed auxiliary functions and leveraging two-sided Polyak--Łojasiewicz (PL) and Quadratic Growth (QG) conditions to characterize the convergence behavior. Under these conditions, it is shown that the Stochastic Alternating Gradient Descent Ascent (SAGDA) algorithm achieves a convergence rate of $\mathcal{O}\left(1/K\right)$, where $K$ denotes the number of iterations. Notably, this result matches convergence rates typically obtained in (weakly) convex--concave minimax settings while requiring significantly milder geometric assumptions. The theoretical results are further validated through empirical experiments on realistic examples.
SN  - 3068-9082
PB  - Institute of Central Computation and Knowledge
LA  - English
ER  -

BibTeX Format

Compatible with LaTeX, BibTeX, and other reference managers

BibTeX format data for LaTeX and reference managers

@article{Zhang2025On,
  author = {Xuelin Zhang},
  title = {On the Convergence of Nonconcave-Nonconvex Max-Min Optimization Problem},
  journal = {Journal of Numerical Simulations in Physics and Mathematics},
  year = {2025},
  volume = {1},
  number = {2},
  pages = {76-83},
  doi = {10.62762/JNSPM.2025.112121},
  url = {https://www.icck.org/article/abs/JNSPM.2025.112121},
  abstract = {Despite extensive study of max--min problems, convergence analysis for the challenging nonconvex--nonconcave setting remains limited. This paper addresses the convergence analysis of nonconvex--nonconcave max--min problems. A novel analytical framework is developed by employing carefully constructed auxiliary functions and leveraging two-sided Polyak--Łojasiewicz (PL) and Quadratic Growth (QG) conditions to characterize the convergence behavior. Under these conditions, it is shown that the Stochastic Alternating Gradient Descent Ascent (SAGDA) algorithm achieves a convergence rate of \$\mathcal{O}\left(1/K\right)\$, where \$K\$ denotes the number of iterations. Notably, this result matches convergence rates typically obtained in (weakly) convex--concave minimax settings while requiring significantly milder geometric assumptions. The theoretical results are further validated through empirical experiments on realistic examples.},
  keywords = {max-min optimization, convergence guarantee, nonconvex-nonconcave problems, two-sided polyak-lojasiewicz, quadratic growth},
  issn = {3068-9082},
  publisher = {Institute of Central Computation and Knowledge}
}

Article Metrics

Citations:

Google Scholar

Crossref

Scopus

Web of Science

Article Access Statistics:

PDF Downloads: 15

Publisher's Note

ICCK stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and Permissions

Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.

Journal of Numerical Simulations in Physics and Mathematics

ISSN: 3068-9082 (Online) | ISSN: 3068-9074 (Print)

Email: [email protected]

Portico

All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/

Google Scholar

Crossref

Scopus

Web of Science

We use cookies