Computational Environmental Heat Transfer Home About Editors Current Issue
-
CiteScore
-
Impact Factor
  1. Home
  2. Journals
  3. Computational Environmental Heat Transfer
  4. Volume 1, Issue 1
Hybrid Nanofluid Heat Transfer Adjacent to Vertical Permeable Surface in the Presence of Thermal Boundary Slip
Research Article | Published: 21 June 2025
Computational Environmental Heat Transfer Volume 1, Issue 1, 2025: 39-50
Volume 1, Issue 1, Computational Environmental Heat Transfer
Volume 1, Issue 1, 2025
Submit Manuscript Edit a Special Issue
Article QR Code
Article QR Code
Scan the QR code for reading
Popular articles
Research on A Ship Trajectory Classification Method Based on Deep Learning Bridging Modalities: A Survey of Cross-Modal Image-Text Retrieval A Mimic Fusion Algorithm for Dual Channel Video Based on Possibility Distribution Synthesis Theory YOLOv7-Bw: A Dense Small Object Efficient Detector Based on Remote Sensing Image Deep Prediction Network Based on Covariance Intersection Fusion for Sensor Data Visual Feature Extraction and Tracking Method Based on Corner Flow Detection Inaugural Editorial of the Chinese Journal of Information Fusion YOLOv8-Lite: A Lightweight Object Detection Model for Real-time Autonomous Driving Systems Short and Long-Term Renewable Electricity Demand Forecasting Based on CNN-Bi-GRU Model Simultaneous Spatiotemporal Bias Compensation and Data Fusion for Asynchronous Multisensor Systems
Computational Environmental Heat Transfer, Volume 1, Issue 1, 2025: 39-50

Open Access | Research Article | 21 June 2025
Hybrid Nanofluid Heat Transfer Adjacent to Vertical Permeable Surface in the Presence of Thermal Boundary Slip
by
Uzma Ahmad Uzma Ahmad 1 *
Kainat Jafri Kainat Jafri 1
1 Department of Mathematics, Faculty of Science, University of Sargodha, Sargodha 40100, Pakistan
* Corresponding Author: Uzma Ahmad, [email protected]
DOI: 10.62762/CEHT.2025.611372
Received: 26 March 2025, Accepted: 07 May 2025, Published: 21 June 2025  
   PDF  (1.39 MB) Full-Text HTML XML
Article Metrics Cite This Article
Abstract
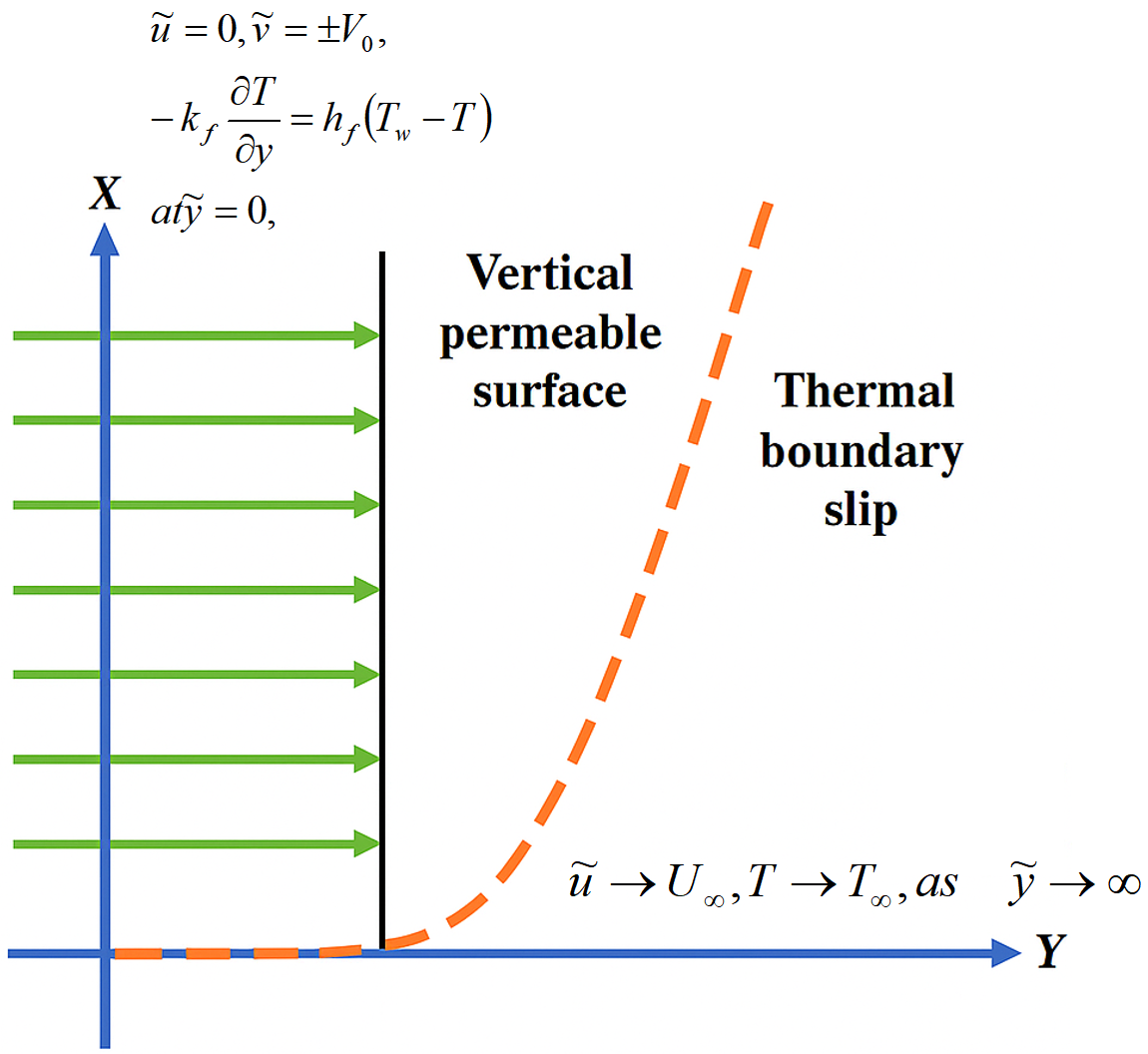
The class of fluid known as hybrid nanofluid has numerous engineering applications in the thermal industry. This study is focused on the heat transmission of the hybrid nanofluid adjacent to a vertical permeable surface by incorporating thermal boundary slip. To support this analysis, a mathematical framework has been established, presenting the problem in terms of coupled nonlinear partial differential equations. These equations have been transformed into a system of dimensionless partial differential equations using appropriate dimensionless variables. Furthermore, the finite difference technique has been employed to obtain the appropriate results. The effects of various dimensionless engineering physical parameters related to hybrid nanofluids have been examined in terms of heat transient rate, coefficient of skin friction, velocity, and temperature profiles. The findings are summarized in both graphical and tabular formats. It is keenly observed that, as the numeric values of transpiration parameter (xi_i) rise, the inclusion of thermal boundary slip leads to an augmentation of velocity and thermal profile at the surface under the effects of both suction and injection. However, an enhancement in the Prandtl number (P_r) results in a decline in velocity profile and an improvement in temperature distribution for both suction and injection.
Graphical Abstract
Hybrid Nanofluid Heat Transfer Adjacent to Vertical Permeable Surface in the Presence of Thermal Boundary Slip
Keywords
hybrid nanofluid
permeable surface
thermal boundary slip
finite difference technique
Data Availability Statement
Data will be made available on request.
Funding
This work was supported without any funding.
Conflicts of Interest
The authors declare no conflicts of interest.
Ethical Approval and Consent to Participate
Not applicable.
References
  1. Clarke, J. F. & Riley, N. (1975). Natural convection induced in a gas by the presence of a hot porous horizontal surface. The Quarterly Journal of Mechanics and Applied Mathematics, 28(4), 373-396.
    [CrossRef]   [Google Scholar]
  2. Schlichting, H., Kestin, J. & Street, R. L. (1980). Boundary-layer theory (7th ed.). McGraw-Hill.
    [Google Scholar]
  3. Roganov, P. S., Zabolotsky, V. P., Shishov, E. V. & Leontiev, A. I. (1984). Some aspects of turbulent heat transfer in accelerated flows on permeable surfaces. International Journal of Heat and Mass Transfer, 27(8), 1251-1259.
    [CrossRef]   [Google Scholar]
  4. Chaudhary, M. A., Merkin, J. H. & Pop, I. (1995). Similarity solutions in free convection boundary-layer flows adjacent to vertical permeable surfaces in porous media: II prescribed surface heat flux. Heat and Mass Transfer, 30(5), 341-347.
    [CrossRef]   [Google Scholar]
  5. Eastman, J. A. (1999). Novel thermal properties of nanostructured materials (Technical Report ANL/MSD/CP-96711). Argonne National Lab.
    [Google Scholar]
  6. Hussain, S., Hossain, M. A. & Wilson, M. (2000). Natural convection flow from a vertical permeable flat plate with variable surface temperature and species concentration. Engineering Computations, 17(7), 789-812.
    [CrossRef]   [Google Scholar]
  7. Yu, S. & Ameel, T. A. (2001). Slip-flow heat transfer in rectangular microchannels. International Journal of Heat and Mass Transfer, 44(22), 4225-4234.
    [CrossRef]   [Google Scholar]
  8. Ali, M. & Al-Yousef, F. (2002). Laminar mixed convection boundary layers induced by a linearly stretching permeable surface. International Journal of Heat and Mass Transfer, 45(21), 4241-4250.
    [CrossRef]   [Google Scholar]
  9. Andersson, H. I. (2002). Slip flow past a stretching surface. Acta Mechanica, 158(1-2), 121-125.
    [CrossRef]   [Google Scholar]
  10. Khanafer, K., Vafai, K. & Lightstone, M. (2003). Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. International Journal of Heat and Mass Transfer, 46(19), 3639-3653.
    [CrossRef]   [Google Scholar]
  11. Maiga, S. E. B., Palm, S. J., Nguyen, C. T., Roy, G. & Galanis, N. (2005). Heat transfer enhancement by using nanofluids in forced convection flows. International Journal of Heat and Fluid Flow, 26(4), 530-546.
    [CrossRef]   [Google Scholar]
  12. Martin, M. J. & Boyd, I. D. (2006). Momentum and heat transfer in a laminar boundary layer with slip flow. Journal of Thermophysics and Heat Transfer, 20(4), 710-719.
    [CrossRef]   [Google Scholar]
  13. Ariel, P. D., Hayat, T. & Asghar, S. (2006). The flow of an elastico-viscous fluid past a stretching sheet with partial slip. Acta Mechanica, 187(1-4), 29-35.
    [CrossRef]   [Google Scholar]
  14. Berg, S., Cense, A. W., Hofman, J. P. & Smits, R. M. M. (2008). Two-phase flow in porous media with slip boundary condition. Transport in Porous Media, 74, 275-292.
    [CrossRef]   [Google Scholar]
  15. Abu-Nada, E., Masoud, Z. & Hijazi, A. (2008). Natural convection heat transfer enhancement in horizontal concentric annuli using nanofluids. International Communications in Heat and Mass Transfer, 35(5), 657-665.
    [CrossRef]   [Google Scholar]
  16. Ishak, A., Nazar, R. & Pop, I. (2009). The effects of transpiration on the flow and heat transfer over a moving permeable surface in a parallel stream. Chemical Engineering Journal, 148(1), 63-67.
    [CrossRef]   [Google Scholar]
  17. Martin, M. J. & Boyd, I. D. (2010). Falkner-Skan flow over a wedge with slip boundary conditions. Journal of Thermophysics and Heat Transfer, 24(2), 263-270.
    [CrossRef]   [Google Scholar]
  18. Ishak, A. (2010). Similarity solutions for flow and heat transfer over a permeable surface with convective boundary condition. Applied Mathematics and Computation, 217(2), 837-842.
    [CrossRef]   [Google Scholar]
  19. Abu-Nada, E., Masoud, Z., Oztop, H. F. & Campo, A. (2010). Effect of nanofluid variable properties on natural convection in enclosures. International Journal of Thermal Sciences, 49(3), 479-491.
    [CrossRef]   [Google Scholar]
  20. Aziz, A. (2010). Hydrodynamic and thermal slip flow boundary layers over a flat plate with constant heat flux boundary condition. Communications in Nonlinear Science and Numerical Simulation, 15(3), 573-580.
    [CrossRef]   [Google Scholar]
  21. Rahman, M. M., Aziz, A. & Al-Lawatia, M. A. (2010). Heat transfer in micropolar fluid along an inclined permeable plate with variable fluid properties. International Journal of Thermal Sciences, 49(6), 993-1002.
    [CrossRef]   [Google Scholar]
  22. Ashraf, M., Asghar, S., & Hossain, M. A. (2010). Thermal radiation effects on hydromagnetic mixed convection flow along a magnetized vertical porous plate. Mathematical Problems in Engineering, 2010, 686594.
    [CrossRef]   [Google Scholar]
  23. Sheikhzadeh, G. A., Arefmanesh, A., Kheirkhah, M. H. & Abdollahi, R. (2011). Natural convection of Cu-water nanofluid in a cavity with partially active side walls. European Journal of Mechanics-B/Fluids, 30(2), 166-176.
    [CrossRef]   [Google Scholar]
  24. Khan, W. A. & Aziz, A. (2011). Natural convection flow of a nanofluid over a vertical plate with uniform surface heat flux. International Journal of Thermal Sciences, 50(7), 1207-1214.
    [CrossRef]   [Google Scholar]
  25. Su, X. H. & Zheng, L. C. (2011). Approximate solutions to MHD Falkner-Skan flow over permeable wall. Applied Mathematics and Mechanics, 32(4), 401-408.
    [CrossRef]   [Google Scholar]
  26. Suresh, S., Venkitaraj, K. P., Selvakumar, P., & Chandrasekar, M. (2012). Effect of Al2O3–Cu/water hybrid nanofluid in heat transfer. Experimental Thermal and Fluid Science, 38, 54-60.
    [CrossRef]   [Google Scholar]
  27. Cortell, R. (2012). Heat transfer in a fluid through a porous medium over a permeable stretching surface with thermal radiation and variable thermal conductivity. The Canadian Journal of Chemical Engineering, 90(5), 1347-1355.
    [CrossRef]   [Google Scholar]
  28. Alvarino, P. F., Jabardo, J. S., Arce, A. & Galdo, M. L. (2012). Heat transfer enhancement in nanofluids: A numerical approach. Journal of Physics: Conference Series, 395, 012116.
    [CrossRef]   [Google Scholar]
  29. Ashraf, M., Asghar, S. & Hossain, M. A. (2012). Computational study of combined effects of conduction-radiation and hydromagnetics on natural convection flow past magnetized permeable plate. Applied Mathematics and Mechanics, 33(6), 731-748.
    [CrossRef]   [Google Scholar]
  30. Huminic, G. & Huminic, A. (2012). Application of nanofluids in heat exchangers: A review. Renewable and Sustainable Energy Reviews, 16(8), 5625-5638.
    [CrossRef]   [Google Scholar]
  31. Noghrehabadi, A., Pourrajab, R. & Ghalambaz, M. (2012). Effect of partial slip boundary condition on the flow and heat transfer of nanofluids past stretching sheet prescribed constant wall temperature. International Journal of Thermal Sciences, 54, 253-261.
    [CrossRef]   [Google Scholar]
  32. Ibrahim, W. & Shankar, B. (2013). MHD boundary layer flow and heat transfer of a nanofluid past a permeable stretching sheet with velocity, thermal and solutal slip boundary conditions. Computers & Fluids, 75, 1-10.
    [CrossRef]   [Google Scholar]
  33. Labib, M. N., Nine, M. J., Afrianto, H., Chung, H. & Jeong, H. (2013). Numerical investigation on effect of base fluids and hybrid nanofluid in forced convective heat transfer. International Journal of Thermal Sciences, 71, 163-171.
    [CrossRef]   [Google Scholar]
  34. Abolbashari, M. H., Freidoonimehr, N., Nazari, F. & Rashidi, M. M. (2014). Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nano-fluid. Powder Technology, 267, 256-267.
    [CrossRef]   [Google Scholar]
  35. Mahdi, R. A., Mohammed, H. A., Munisamy, K. M. & Saeid, N. H. (2015). Review of convection heat transfer and fluid flow in porous media with nanofluid. Renewable and Sustainable Energy Reviews, 41, 715-734.
    [CrossRef]   [Google Scholar]
  36. Sarkar, J., Ghosh, P. & Adil, A. (2015). A review on hybrid nanofluids: Recent research, development and applications. Renewable and Sustainable Energy Reviews, 43, 164-177.
    [CrossRef]   [Google Scholar]
  37. Sidik, N. A. C., Adamu, I. M., Jamil, M. M., Kefayati, G. H. R., Mamat, R. & Najafi, G. (2016). Recent progress on hybrid nanofluids in heat transfer applications: A comprehensive review. International Communications in Heat and Mass Transfer, 78, 68-79.
    [CrossRef]   [Google Scholar]
  38. Hussain, A. M. (2017). Thermal performance and thermal properties of hybrid nanofluid laminar flow in a double pipe heat exchanger. Experimental Thermal and Fluid Science, 88, 37-45.
    [CrossRef]   [Google Scholar]
  39. Kasaeian, A., Daneshazarian, R., Mahian, O., Kolsi, L., Chamkha, A. J., Wongwises, S. & Pop, I. (2017). Nanofluid flow and heat transfer in porous media: A review of the latest developments. International Journal of Heat and Mass Transfer, 107, 778-791.
    [CrossRef]   [Google Scholar]
  40. Fakour, M., Ganji, D. D., Khalili, A. & Bakhshi, A. (2017). Heat transfer in nanofluid MHD flow in a channel with permeable walls. Heat Transfer Research, 48(3), 209-222.
    [CrossRef]   [Google Scholar]
  41. Sundar, L. S., Sharma, K. V., Singh, M. K. & Sousa, A. C. M. (2017). Hybrid nanofluids preparation, thermal properties, heat transfer and friction factor—A review. Renewable and Sustainable Energy Reviews, 68, 185-198.
    [CrossRef]   [Google Scholar]
  42. Yarmand, H., Zulkifli, N. W. B. M., Gharehkhani, S., Shirazi, S. F. S., Alrashed, A. A., Ali, M. A. B. & Kazi, S. N. (2017). Convective heat transfer enhancement with graphene nano platelet/platinum hybrid nanofluid. International Communications in Heat and Mass Transfer, 88, 120-125.
    [CrossRef]   [Google Scholar]
  43. Bhattad, A., Sarkar, J. & Ghosh, P. (2018). Discrete phase numerical model and experimental study of hybrid nanofluid heat transfer and pressure drop in plate heat exchanger. International Communications in Heat and Mass Transfer, 91, 262-273.
    [CrossRef]   [Google Scholar]
  44. Minea, A. A. & Moldoveanu, M. G. (2018). Overview of hybrid nanofluids development and benefits. Journal of Engineering Thermophysics, 27, 507-514.
    [CrossRef]   [Google Scholar]
  45. Aly, E. H. & Pop, I. (2019). MHD flow and heat transfer over a permeable stretching/shrinking sheet in a hybrid nanofluid with a convective boundary condition. International Journal of Numerical Methods for Heat & Fluid Flow, 29(9), 3012-3038.
    [CrossRef]   [Google Scholar]
  46. Kumar, K. A., Sugunamma, V., Sandeep, N. & Mustafa, M. (2019). Simultaneous solutions for first order and second order slips on micropolar fluid flow across a convective surface in the presence of Lorentz force and variable heat source/sink. Scientific Reports, 9(1), 14706.
    [CrossRef]   [Google Scholar]
  47. Sidik, N. A. C., Adamu, I. M. & Jamil, M. M. (2019). Preparation methods and thermal performance of hybrid nanofluids. Journal of Advanced Research in Materials Science, 56(1), 1-10.
    [Google Scholar]
  48. Babar, H. & Ali, H. M. (2019). Towards hybrid nanofluids: Preparation, thermophysical properties, applications, and challenges. Journal of Molecular Liquids, 281, 598-633.
    [CrossRef]   [Google Scholar]
  49. Manjunatha, S., Kuttan, B. A., Jayanthi, S., Chamkha, A. & Gireesha, B. J. (2019). Heat transfer enhancement in the boundary layer flow of hybrid nanofluids due to variable viscosity and natural convection. Heliyon, 5(4), e01469.
    [CrossRef]   [Google Scholar]
  50. Ashraf, M., Khan, A. & Gorla, R. S. R. (2019). Natural convection boundary layer flow of nanofluids around different stations of the sphere and into the plume above the sphere. Heat Transfer-Asian Research, 48(3), 1127-1148.
    [CrossRef]   [Google Scholar]
  51. Shafiq, A., Rasool, G. & Khalique, C. M. (2020). Significance of thermal slip and convective boundary conditions in three dimensional rotating Darcy-Forchheimer nanofluid flow. Symmetry, 12(5), 741.
    [CrossRef]   [Google Scholar]
  52. Roy, N. C. & Pop, I. (2020). Flow and heat transfer of a second-grade hybrid nanofluid over a permeable stretching/shrinking sheet. The European Physical Journal Plus, 135(9), 768.
    [CrossRef]   [Google Scholar]
  53. Waini, I., Ishak, A.& Pop, I. (2020). MHD flow and heat transfer of a hybrid nanofluid past a permeable stretching/shrinking wedge. Applied Mathematics and Mechanics, 41(3), 507-520.
    [CrossRef]   [Google Scholar]
  54. Jeelani, M. B. & Abbas, A. (2023). $Al_2O_3$-Cu ethylene glycol-based magnetohydrodynamic non-Newtonian Maxwell hybrid nano-fluid flow with suction effects in a porous space: Energy saving by solar radiation. Symmetry, 15(9), 1794.
    [CrossRef]   [Google Scholar]
  55. Bhattad, A., Atgur, V., Rao, B. N., Banapurmath, N. R., Khan, T. M. Y., Vadlamudi, C. & Ayachit, N. H. (2023). Review on Mono and Hybrid Nanofluids: Preparation, Properties, Investigation, and Applications in IC Engines and Heat Transfer. Energies, 16(7), 3189.
    [CrossRef]   [Google Scholar]
Cite This Article
APA Style
Ahmad, U., & Jafri, K. (2025). Hybrid Nanofluid Heat Transfer Adjacent to Vertical Permeable Surface in the Presence of Thermal Boundary Slip. Computational Environmental Heat Transfer, 1(1), 39–50. https://doi.org/10.62762/CEHT.2025.611372
Article Metrics
Citations:

Google Scholar
0

Crossref

0

Scopus

0

Web of Science

0
Article Access Statistics:
Views: 136
PDF Downloads: 39
Publisher's Note
ICCK stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and Permissions
CC BY Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
Computational Environmental Heat Transfer

Computational Environmental Heat Transfer

ISSN: 3068-5486 (Online)

Email: [email protected]

Portico

Portico

All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/