Multi-strategy Enhanced Grey Wolf Optimizer for Numerical Optimization and Its Application to Feature Selection

Wenmin Xu; Wen Long

doi:10.62762/JMIA.2025.522565

CiteScore

Impact Factor

Volume 1, Issue 1, Journal of Mathematics and Interdisciplinary Applications

Volume 1, Issue 1, 2025

Submit Manuscript Edit a Special Issue

Article QR Code

Scan the QR code for reading

Popular articles

Case Studies on Integrating Artificial Intelligence in Finance to Transform Decision Making and Risk Management for Enhanced Financial Outcomes Reinforcement Learning for Prompt Optimization in Language Models: A Comprehensive Survey of Methods, Representations, and Evaluation Challenges AI and the Future of Education: Advancing Personalized Learning and Intelligent Tutoring Systems Plant Disease Detection Using Deep Learning Techniques Modeling Brain Functional Networks Using Graph Neural Networks: A Review and Clinical Application Bridging Modalities: A Survey of Cross-Modal Image-Text Retrieval Research on A Ship Trajectory Classification Method Based on Deep Learning Enhancing Fake News Detection with a Hybrid NLP-Machine Learning Framework Acrylamide in Food: Sources and Prevention Analyzing the Translation and Impact of Popular Science Literature in China: A Case Study Approach

Journal of Mathematics and Interdisciplinary Applications, Volume 1, Issue 1, 2025: 51-71

Open Access | Research Article | 29 November 2025

Multi-strategy Enhanced Grey Wolf Optimizer for Numerical Optimization and Its Application to Feature Selection

Wenmin Xu 1

Wen Long 1 *

1 School of Mathematics and Statistics, Guizhou University of Finance and Economics, Guiyang 550025, China

* Corresponding Author: Wen Long, [email protected]

DOI: 10.62762/JMIA.2025.522565

Received: 02 September 2025, Accepted: 28 October 2025, Published: 29 November 2025

PDF (1.63 MB)

Article Metrics Cite This Article

Abstract

Grey wolf optimizer (GWO) is an effective meta-heuristic technique which has been widely utilized to solve numerical optimization as well as real-world applications. However, GWO has some shortcomings, i.e., low solution accuracy, slow convergence, and easy stagnation at local optima in solving complex problems. To tackle these shortcomings, an enhanced GWO called EGWO is developed in this study. This enhancement is achieved by embedding three novel strategies into the basic GWO to improve its performance. Firstly, a new transition mechanism is designed instead of the original strategy to obtain a good transition from the exploration to exploitation. Secondly, the cuckoo search algorithm is introduced for the decision layer individuals ($\alpha$, $\beta$, and $\delta$) to further improve the local search capability. Thirdly, an adaptive position search equation is proposed by using a dynamical parameter to generate new potential candidate position. The effectiveness of EGWO is verified on 25 classical benchmarks, three engineering problems, and 16 feature selection problems. The results show that EGWO performs better than the original GWO and other meta-heuristic methods in terms of solution accuracy and convergence speed.

Graphical Abstract

Keywords

grey wolf optimizer

cuckoo search

numerical optimization

Engineering optimization

feature selection

Data Availability Statement

Data will be made available on request.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grant 12361106; in part by the Guizhou Provincial Science and Technology Plan Key Projects of Qiankehe Jichu under Grant ZK[2023]003; in part by the Guizhou Provincial High Level Innovative Talent Training Plan Project of Qiankehe Platform Talent under Grant GCC[2023]006.

Conflicts of Interest

The authors declare no conflicts of interest.

Ethical Approval and Consent to Participate

Not applicable.

References

Gharehchopogh, F. S., Nadimi-Shahraki, M. H., Barshandeh, S., Abdollahzadeh, B., & Zamani, H. (2023). Cqffa: A chaotic quasi-oppositional farmland fertility algorithm for solving engineering optimization problems. Journal of Bionic Engineering, 20(1), 158-183.
[CrossRef] [Google Scholar]
Abualigah, L., Diabat, A., Svetinovic, D., & Elaziz, M. A. (2023). Boosted Harris Hawks gravitational force algorithm for global optimization and industrial engineering problems. Journal of Intelligent Manufacturing, 34(6), 2693-2728.
[CrossRef] [Google Scholar]
Mirjalili, S., Mirjalili, S. M., & Lewis, A. (2014). Grey wolf optimizer. Advances in Engineering Software, 69, 46–61.
[CrossRef] [Google Scholar]
Nadimi-Shahraki, M. H., Moeini, E., Taghian, S., & Mirjalili, S. (2023). Discrete improved grey wolf optimizer for community detection. Journal of Bionic Engineering, 20(5), 2331-2358.
[CrossRef] [Google Scholar]
Long, W., Cai, S., Jiao, J., Xu, M., & Wu, T. (2020). A hybrid algorithm based on grey wolf optimizer and cuckoo search for parameter extraction of solar photovoltaic models. Energy Conversion and Management, 203, 112243.
[CrossRef] [Google Scholar]
Nuaekaew, K., Artrit, P., Pholdee, N., & Bureerat, S. (2017). Optimal reactive power dispatch problem using a two-archive multi-objective grey wolf optimizer. Expert Systems with Applications, 87, 79–89.
[CrossRef] [Google Scholar]
Makhadmeh, S. N., Khader, A. T., Al-Betar, M. A., Naim, S., Abasi, A. K., & Alyasseri, Z. A. A. (2021). A hybrid grey wolf optimizer with min-conflict algorithm for power scheduling in a smart home. Swarm and Evolutionary Computation, 60, 100793.
[CrossRef] [Google Scholar]
Ahmadi, R., Ekbatanifard, G., & Bayat, P. (2021). A modified grey wolf optimizer-based data clustering algorithm. Applied Artificial Intelligence, 35(1), 63–79.
[CrossRef] [Google Scholar]
Nadimi-Shahraki, M. H., Taghian, S., & Mirjalili, S. (2021). An improved grey wolf optimizer for solving engineering problems. Expert Systems with Applications, 166, 113917.
[CrossRef] [Google Scholar]
Altan, A., Karasu, S., & Zio, E. (2021). A hybrid model for wind speed forecasting combining LSTM neural network, decomposition methods and grey wolf optimizer. Applied Soft Computing, 100, 106996.
[CrossRef] [Google Scholar]
Yu, X., & Wu, X. (2022). Ensemble grey wolf optimizer and its application for image segmentation. Expert Systems with Applications, 209, 118267.
[CrossRef] [Google Scholar]
Abualigah, L., Habash, M., Hanandeh, E. S., Hussein, A. M., Shinwan, M. A., Zitar, R. A., & Jia, H. (2023). Improved reptile search algorithm by salp swarm algorithm for medical image segmentation. Journal of bionic engineering, 20(4), 1766-1790.
[CrossRef] [Google Scholar]
Jia, Y., Qu, L., & Li, X. (2023). Automatic path planning of unmanned combat aerial vehicle based on double-layer coding method with enhanced grey wolf optimizer. Artificial Intelligence Review, 56(10), 12257-12314.
[CrossRef] [Google Scholar]
Manikandan, K. (2019). Diagnosis of diabetes diseases using optimized fuzzy rule set by grey wolf optimization. Pattern Recognition Letters, 125, 432-438.
[CrossRef] [Google Scholar]
Singh, D., & Dhillon, J. S. (2019). Ameliorated grey wolf optimizer for economic load dispatch problem. Energy, 169, 398–419.
[CrossRef] [Google Scholar]
Srikanth, K., Panwar, L. K., Panigrahi, B. K., Herrera-Viedma, E., Sangaiah, A. K., & Wang, G. (2018). Quantum-inspired binary grey wolf optimizer for unit commitment problem. Computers & Electrical Engineering, 70, 243–260.
[CrossRef] [Google Scholar]
Ebrahimi, S. M., Hasanzadeh, S., & Khatibi, S. (2023). Parameter identification of fuel cell using repairable grey wolf optimization algorithm. Applied Soft Computing, 147, 110791.
[CrossRef] [Google Scholar]
Gharehchopogh, F. S. (2022). An improved tunicate swarm algorithm with best-random mutation strategy for global optimization problems. Journal of Bionic Engineering, 19(4), 1177-1202.
[CrossRef] [Google Scholar]
Wang, Z., Shu, L., Yang, S., Zeng, Z., He, D., & Chan, S. (2025). Multi-population dynamic grey wolf optimizer based on dimension learning and Laplace Mutation for global optimization. Expert Systems with Applications, 265, 125863.
[CrossRef] [Google Scholar]
Heidari, A. A., & Pahlavani, P. (2017). Modified grey wolf optimizer with Lévy flight for optimization tasks. Applied Soft Computing, 60, 115–134.
[CrossRef] [Google Scholar]
Hu, P., Pan, J. S., & Chu, S. C. (2020). Improved binary grey wolf optimizer and its application for feature selection. Knowledge-Based Systems, 195, 105746.
[CrossRef] [Google Scholar]
Mittal, N., Singh, U., & Sohi, B. S. (2016). Modified grey wolf optimizer for global engineering optimization. Applied computational intelligence and soft computing, 2016(1), 7950348.
[CrossRef] [Google Scholar]
Singh, N. (2020). A modified variant of grey wolf optimizer. Scientia Iranica, 27(3), 1450-1466.
[CrossRef] [Google Scholar]
Rodríguez, L., Castillo, O., Soria, J., Melin, P., Valdez, F., Gonzalez, C. I., & Soto, J. (2017). Fuzzy hierarchical operator in grey wolf optimizer. Applied Soft Computing, 57, 315–328.
[CrossRef] [Google Scholar]
Daniel, E., Anitha, J., & Gnanaraj, J. (2017). Optimum laplacian wavelet mask based medical image using hybrid cuckoo search–grey wolf optimization algorithm. Knowledge-Based Systems, 131, 58-69.
[CrossRef] [Google Scholar]
Yu, X., Zhao, Q., Lin, Q., & Wang, T. (2023). A grey wolf optimizer-based chaotic gravitational search algorithm for global optimization. The Journal of Supercomputing, 79(3), 2691-2739.
[CrossRef] [Google Scholar]
Sundaramurthy, S., & Jayavel, P. (2020). A hybrid grey wolf optimization and particle swarm optimization with C4. 5 approach for prediction of rheumatoid arthritis. Applied Soft Computing, 94, 106500.
[CrossRef] [Google Scholar]
Singh, G., & Singh, U. (2023). Hybrid binary grey wolf naked mole-rat algorithm for fragment-type UWB antenna optimization using time-varying transfer functions. Expert Systems with Applications, 232, 120802.
[CrossRef] [Google Scholar]
Arora, S., Singh, H., Sharma, M., Sharma, S., & Anand, P. (2019). A new hybrid algorithm based on grey wolf optimization and crow search algorithm for unconstrained function optimization and feature selection. IEEE Access, 7, 26343-26361.
[CrossRef] [Google Scholar]
Zhou, J., Huang, S., Zhou, T., Armaghani, D. J., & Qiu, Y. (2022). Employing a genetic algorithm and grey wolf optimizer for optimizing RF models to evaluate soil liquefaction potential. Artificial intelligence review, 55(7), 5673-5705.
[CrossRef] [Google Scholar]
Shilaja, C., & Arunprasath, T. (2019). Internet of medical things-load optimization of power flow based on hybrid enhanced grey wolf optimization and dragonfly algorithm. Future Generation Computer Systems, 98, 319-330.
[CrossRef] [Google Scholar]
Hemalatha, S., Banu, G., & Indirajith, K. (2023). Design and investigation of PV string/central architecture for bayesian fusion technique using grey wolf optimization and flower pollination optimized algorithm. Energy Conversion and Management, 286, 117078.
[CrossRef] [Google Scholar]
Yang, Q., Liu, J., Wu, Z., & He, S. (2023). A fusion algorithm based on whale and grey wolf optimization algorithm for solving real-world optimization problems. Applied Soft Computing, 146, 110701.
[CrossRef] [Google Scholar]
Karakoyun, M., Ozkis, A., & Kodaz, H. (2020). A new algorithm based on gray wolf optimizer and shuffled frog leaping algorithm to solve the multi-objective optimization problems. Applied Soft Computing, 96, 106560.
[CrossRef] [Google Scholar]
Makhadmeh, S. N., Abasi, A. K., & Al-Betar, M. A. (2022). Hybrid multi-verse optimizer with grey wolf optimizer for power scheduling problem in smart home using IoT. The Journal of Supercomputing, 78(9), 11794-11829.
[CrossRef] [Google Scholar]
Dhargupta, S., Ghosh, M., Mirjalili, S., & Sarkar, R. (2020). Selective opposition-based grey wolf optimizer. Expert Systems with Applications, 151, 113389.
[CrossRef] [Google Scholar]
Khanum, R. A., Jan, M. A., Aldegheishem, A., Mehmood, A., Alrajeh, N., & Khanan, A. (2019). Two new improved variants of grey wolf optimizer for unconstrained optimization. IEEE Access, 8, 30805-30825.
[CrossRef] [Google Scholar]
Gupta, S., & Deep, K. (2019). A novel random walk grey wolf optimizer. Swarm and evolutionary computation, 44, 101-112.
[CrossRef] [Google Scholar]
Abdel-Basset, M., El-Shahat, D., El-Henawy, I., De Albuquerque, V. H. C., & Mirjalili, S. (2020). A new fusion of grey wolf optimizer algorithm with a two-phase mutation for feature selection. Expert Systems with Applications, 139, 112824.
[CrossRef] [Google Scholar]
Ahmed, R., Rangaiah, G. P., Mahadzir, S., Mirjalili, S., Hassan, M. H., & Kamel, S. (2023). Memory, evolutionary operator, and local search based improved Grey Wolf Optimizer with linear population size reduction technique. Knowledge-Based Systems, 264, 110297.
[CrossRef] [Google Scholar]
Kumar, V., & Kumar, D. (2017). An astrophysics-inspired grey wolf algorithm for numerical optimization and its application to engineering design problems. Advances in Engineering Software, 112, 231-254.
[CrossRef] [Google Scholar]
Rodríguez, A., Camarena, O., Cuevas, E., Aranguren, I., Valdivia-G, A., Morales-Castañeda, B., ... & Pérez-Cisneros, M. (2021). Group-based synchronous-asynchronous grey wolf optimizer. Applied Mathematical Modelling, 93, 226-243.
[CrossRef] [Google Scholar]
Seyyedabbasi, A., & Kiani, F. (2021). I-GWO and Ex-GWO: improved algorithms of the Grey Wolf Optimizer to solve global optimization problems. Engineering with Computers, 37(1), 509-532.
[CrossRef] [Google Scholar]
Sang-To, T., Le-Minh, H., Mirjalili, S., Wahab, M. A., & Cuong-Le, T. (2022). A new movement strategy of grey wolf optimizer for optimization problems and structural damage identification. Advances in Engineering Software, 173, 103276.
[CrossRef] [Google Scholar]
Yang, X. S., & Deb, S. (2010). Engineering optimisation by cuckoo search. International Journal of Mathematical Modelling and Numerical Optimisation, 1(4), 330-343.
[CrossRef] [Google Scholar]
Yang, X. S., & Deb, S. (2013). Multiobjective cuckoo search for design optimization. Computers & Operations Research, 40(6), 1616-1624.
[CrossRef] [Google Scholar]
Nickabadi, A., Ebadzadeh, M. M., & Safabakhsh, R. (2011). A novel particle swarm optimization algorithm with adaptive inertia weight. Applied soft computing, 11(4), 3658-3670.
[CrossRef] [Google Scholar]
Hansen, N., & Ostermeier, A. (2001). Completely derandomized self-adaptation in evolution strategies. Evolutionary computation, 9(2), 159-195.
[CrossRef] [Google Scholar]
Rahnamayan, S., Tizhoosh, H. R., & Salama, M. M. (2008). Opposition-based differential evolution. IEEE Transactions on Evolutionary computation, 12(1), 64-79.
[CrossRef] [Google Scholar]
Mirjalili, S., & Lewis, A. (2016). The whale optimization algorithm. Advances in engineering software, 95, 51-67.
[CrossRef] [Google Scholar]
Heidari, A. A., Mirjalili, S., Faris, H., Aljarah, I., Mafarja, M., & Chen, H. (2019). Harris hawks optimization: Algorithm and applications. Future generation computer systems, 97, 849-872.
[CrossRef] [Google Scholar]
Lu, C., Gao, L., Li, X., Hu, C., Yan, X., & Gong, W. (2020). Chaotic-based grey wolf optimizer for numerical and engineering optimization problems. Memetic Computing, 12(4), 371–398.
[CrossRef] [Google Scholar]
Deb, K. (2000). An efficient constraint handling method for genetic algorithms. Computer methods in applied mechanics and engineering, 186(2-4), 311-338.
[CrossRef] [Google Scholar]
Zhang, J., & Sanderson, A. C. (2009). JADE: adaptive differential evolution with optional external archive. IEEE Transactions on evolutionary computation, 13(5), 945-958.
[CrossRef] [Google Scholar]
He, Q., & Wang, L. (2007). An effective co-evolutionary particle swarm optimization for constrained engineering design problems. Engineering applications of artificial intelligence, 20(1), 89-99.
[CrossRef] [Google Scholar]
Long, W., Wu, T., Liang, X., & Xu, S. (2019). Solving high-dimensional global optimization problems using an improved sine cosine algorithm. Expert systems with applications, 123, 108-126.
[CrossRef] [Google Scholar]
Gao, W., Liu, S., & Huang, L. (2012). A global best artificial bee colony algorithm for global optimization. Journal of Computational and Applied Mathematics, 236(11), 2741-2753.
[CrossRef] [Google Scholar]
Arora, S., & Anand, P. (2019). Binary butterfly optimization approaches for feature selection. Expert Systems with Applications, 116, 147-160.
[CrossRef] [Google Scholar]
Gharehchopogh, F. S. (2023). An improved Harris Hawks optimization algorithm with multi-strategy for community detection in social network. Journal of Bionic Engineering, 20(3), 1175-1197.
[CrossRef] [Google Scholar]
Long, W., Jiao, J., Liang, X., Wu, T., Xu, M., & Cai, S. (2021). Pinhole-imaging-based learning butterfly optimization algorithm for global optimization and feature selection. Applied Soft Computing, 103, 107146.
[CrossRef] [Google Scholar]
Abualigah, L., & Dulaimi, A. J. (2021). A novel feature selection method for data mining tasks using hybrid sine cosine algorithm and genetic algorithm. Cluster Computing, 24(3), 2161-2176.
[CrossRef] [Google Scholar]
Emary, E., Zawbaa, H. M., & Hassanien, A. E. (2016). Binary ant lion approaches for feature selection. Neurocomputing, 213, 54-65.
[CrossRef] [Google Scholar]
Askarzadeh, A. (2016). A novel metaheuristic method for solving constrained engineering optimization problems: crow search algorithm. Computers & structures, 169, 1-12.
[CrossRef] [Google Scholar]
Shi, Y., & Eberhart, R. (1998, May). A modified particle swarm optimizer. In 1998 IEEE international conference on evolutionary computation proceedings. IEEE world congress on computational intelligence (Cat. No. 98TH8360) (pp. 69-73). IEEE.
[CrossRef] [Google Scholar]
Qais, M. H., Hasanien, H. M., & Alghuwainem, S. (2018). Augmented grey wolf optimizer for grid-connected PMSG-based wind energy conversion systems. Applied Soft Computing, 69, 504-515.
[CrossRef] [Google Scholar]
Joshi, H., & Arora, S. (2017). Enhanced grey wolf optimization algorithm for global optimization. Fundamenta Informaticae, 153(3), 235-264.
[CrossRef] [Google Scholar]

Cite This Article

APA Style

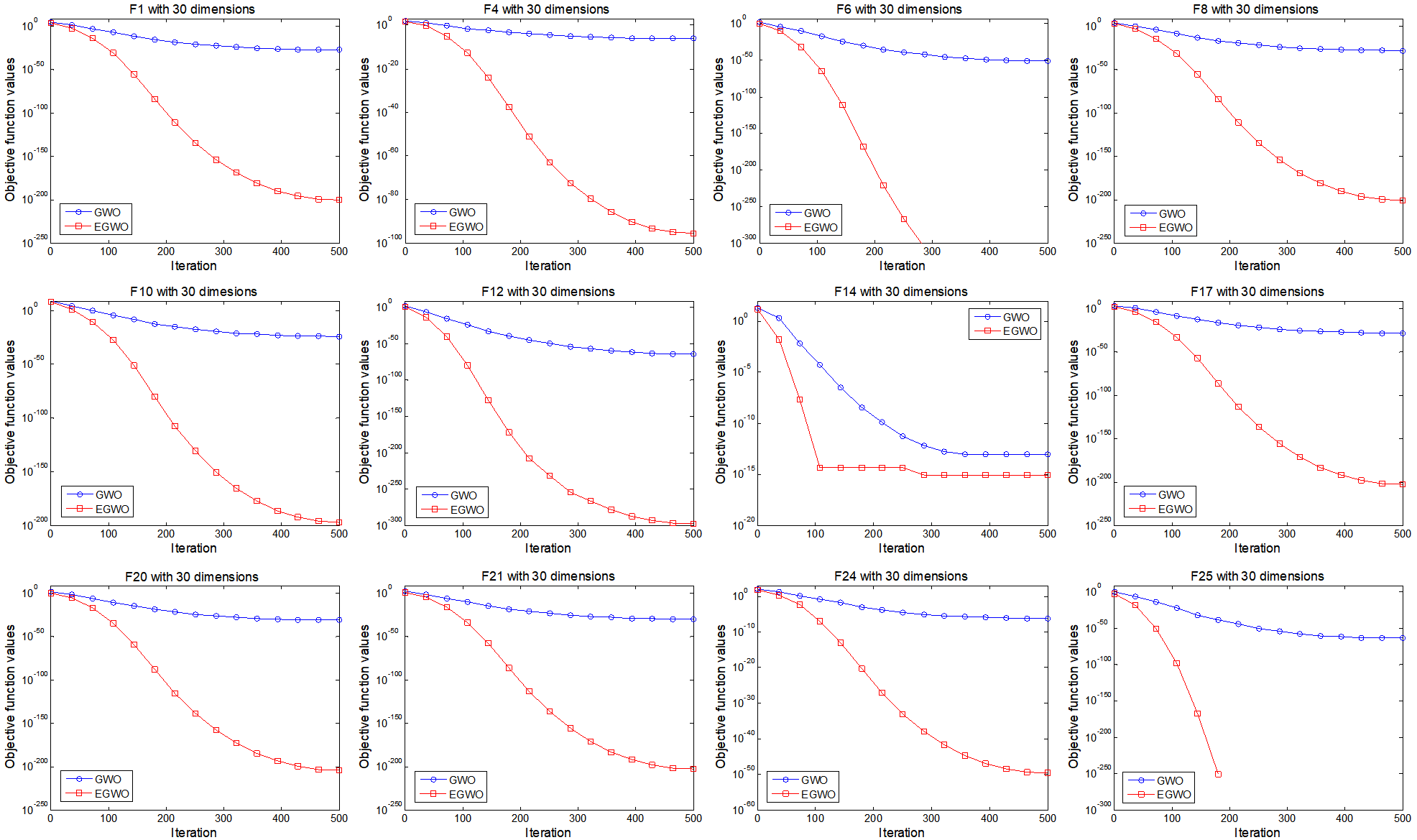
Xu, W., & Long, W. (2025). Multi-strategy Enhanced Grey Wolf Optimizer for Numerical Optimization and Its Application to Feature Selection. Journal of Mathematics and Interdisciplinary Applications, 1(1), 51–71. https://doi.org/10.62762/JMIA.2025.522565

Export Citation

RIS Format

Compatible with EndNote, Zotero, Mendeley, and other reference managers

RIS format data for reference managers

TY  - JOUR
AU  - Xu, Wenmin
AU  - Long, Wen
PY  - 2025
DA  - 2025/11/29
TI  - Multi-strategy Enhanced Grey Wolf Optimizer for Numerical Optimization and Its Application to Feature Selection
JO  - Journal of Mathematics and Interdisciplinary Applications
T2  - Journal of Mathematics and Interdisciplinary Applications
JF  - Journal of Mathematics and Interdisciplinary Applications
VL  - 1
IS  - 1
SP  - 51
EP  - 71
DO  - 10.62762/JMIA.2025.522565
UR  - https://www.icck.org/article/abs/JMIA.2025.522565
KW  - grey wolf optimizer
KW  - cuckoo search
KW  - numerical optimization
KW  - Engineering optimization
KW  - feature selection
AB  - Grey wolf optimizer (GWO) is an effective meta-heuristic technique which has been widely utilized to solve numerical optimization as well as real-world applications. However, GWO has some shortcomings, i.e., low solution accuracy, slow convergence, and easy stagnation at local optima in solving complex problems. To tackle these shortcomings, an enhanced GWO called EGWO is developed in this study. This enhancement is achieved by embedding three novel strategies into the basic GWO to improve its performance. Firstly, a new transition mechanism is designed instead of the original strategy to obtain a good transition from the exploration to exploitation. Secondly, the cuckoo search algorithm is introduced for the decision layer individuals ($\alpha$, $\beta$, and $\delta$) to further improve the local search capability. Thirdly, an adaptive position search equation is proposed by using a dynamical parameter to generate new potential candidate position. The effectiveness of EGWO is verified on 25 classical benchmarks, three engineering problems, and 16 feature selection problems. The results show that EGWO performs better than the original GWO and other meta-heuristic methods in terms of solution accuracy and convergence speed.
SN  - pending
PB  - Institute of Central Computation and Knowledge
LA  - English
ER  -

BibTeX Format

Compatible with LaTeX, BibTeX, and other reference managers

BibTeX format data for LaTeX and reference managers

@article{Xu2025Multistrat,
  author = {Wenmin Xu and Wen Long},
  title = {Multi-strategy Enhanced Grey Wolf Optimizer for Numerical Optimization and Its Application to Feature Selection},
  journal = {Journal of Mathematics and Interdisciplinary Applications},
  year = {2025},
  volume = {1},
  number = {1},
  pages = {51-71},
  doi = {10.62762/JMIA.2025.522565},
  url = {https://www.icck.org/article/abs/JMIA.2025.522565},
  abstract = {Grey wolf optimizer (GWO) is an effective meta-heuristic technique which has been widely utilized to solve numerical optimization as well as real-world applications. However, GWO has some shortcomings, i.e., low solution accuracy, slow convergence, and easy stagnation at local optima in solving complex problems. To tackle these shortcomings, an enhanced GWO called EGWO is developed in this study. This enhancement is achieved by embedding three novel strategies into the basic GWO to improve its performance. Firstly, a new transition mechanism is designed instead of the original strategy to obtain a good transition from the exploration to exploitation. Secondly, the cuckoo search algorithm is introduced for the decision layer individuals (\$\alpha\$, \$\beta\$, and \$\delta\$) to further improve the local search capability. Thirdly, an adaptive position search equation is proposed by using a dynamical parameter to generate new potential candidate position. The effectiveness of EGWO is verified on 25 classical benchmarks, three engineering problems, and 16 feature selection problems. The results show that EGWO performs better than the original GWO and other meta-heuristic methods in terms of solution accuracy and convergence speed.},
  keywords = {grey wolf optimizer, cuckoo search, numerical optimization, Engineering optimization, feature selection},
  issn = {pending},
  publisher = {Institute of Central Computation and Knowledge}
}

Article Metrics

Citations:

Google Scholar

Crossref

Scopus

Web of Science

Article Access Statistics:

PDF Downloads: 33

Publisher's Note

ICCK stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and Permissions

Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.

Journal of Mathematics and Interdisciplinary Applications

ISSN: pending (Online)

Email: [email protected]

Portico

All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/

Google Scholar

Crossref

Scopus

Web of Science

We use cookies