Advances in the Mathematical Theory of WPAA Dynamics for Impulsive High Order Neural Systems in Clifford Algebras

Chaouki Aouiti; Farah Dridi

doi:10.62762/JNDA.2025.838385

Volume 2, Issue 1, Journal of Nonlinear Dynamics and Applications

Volume 2, Issue 1, 2026

Submit Manuscript Edit a Special Issue

Article QR Code

Scan the QR code for reading

Popular articles

Case Studies on Integrating Artificial Intelligence in Finance to Transform Decision Making and Risk Management for Enhanced Financial Outcomes Reservoir Science: A Multi-Coupling Communication Platform to Promote Energy Transformation, Climate Change and Environmental Protection Reinforcement Learning for Prompt Optimization in Language Models: A Comprehensive Survey of Methods, Representations, and Evaluation Challenges From CO$_2$ Sequestration to Hydrogen Storage: Further Utilization of Depleted Gas Reservoirs AI and the Future of Education: Advancing Personalized Learning and Intelligent Tutoring Systems Effects of Crosslinking Agents and Reservoir Conditions on the Propagation of Fractures in Coal Reservoirs During Hydraulic Fracturing The Influence of Geological Factors and Transmission Fluids on the Exploitation of Reservoir Geothermal Resources: Factor Discussion and Mechanism Analysis YOLOv8-Lite: A Lightweight Object Detection Model for Real-time Autonomous Driving Systems Plant Disease Detection Using Deep Learning Techniques Modeling Brain Functional Networks Using Graph Neural Networks: A Review and Clinical Application

Journal of Nonlinear Dynamics and Applications, Volume 2, Issue 1, 2026: 1-12

Free to Read | Research Article | 21 January 2026

Advances in the Mathematical Theory of WPAA Dynamics for Impulsive High Order Neural Systems in Clifford Algebras

Chaouki Aouiti 1 *

Farah Dridi 1

1 GAMA Laboratory (LR21ES10), Department of Mathematics, Faculty of Sciences of Bizerte, University of Carthage, Bizerte 7021, Tunisia

* Corresponding Author: Chaouki Aouiti, [email protected]

DOI: 10.62762/JNDA.2025.838385

ARK: ark:/57805/jnda.2025.838385

Received: 23 October 2025, Accepted: 09 January 2026, Published: 21 January 2026

PDF (889.47 KB)

Article Metrics Cite This Article

Abstract

The primary objective of this work is to establish the existence, uniqueness, and exponential stability of piecewise weighted pseudo–almost automorphic solutions for impulsive high-order Hopfield neural networks formulated within Clifford algebras. Using the Banach fixed-point principle together with a suitably adapted Gronwall–Bellman inequality, we derive novel and verifiable sufficient conditions that ensure these qualitative properties. The main contributions are as follows: (i) this study is the first to analyze weighted pseudo–almost automorphic (WPAA) dynamics for impulsive high-order Hopfield neural networks directly in the Clifford algebra setting, without reducing the model to real-valued components; (ii) it offers a unified framework that accommodates both first- and second-order synaptic interactions under impulsive perturbations and mixed delays; and (iii) the resulting conditions explicitly capture the geometric structure of Clifford-valued states, providing a broader and algebraically consistent formulation compared to real or quaternion-valued models. The theoretical findings are further supported by a numerical example demonstrating their applicability and effectiveness.

Graphical Abstract

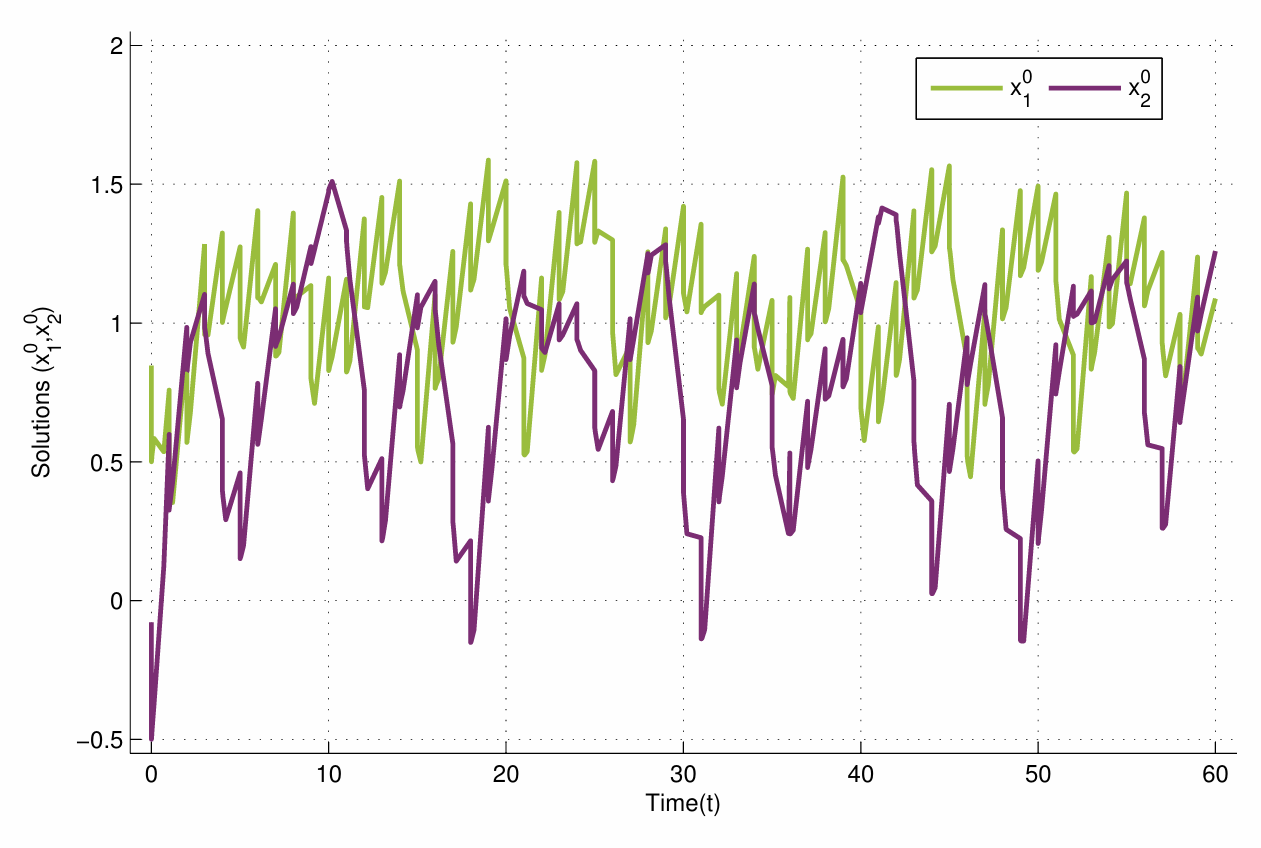
Advances in the Mathematical Theory of WPAA Dynamics for Impulsive High Order Neural Systems in Clifford Algebras

Keywords

impulsive systems

WPAA-functions

HOHNNs

Gronwall–Bellman inequality

exponential stability

clifford algebra

Data Availability Statement

No datasets were generated or analyzed during the current study.

Funding

This work was supported without any funding.

Conflicts of Interest

The authors declare no conflicts of interest.

AI Use Statement

The authors declare that no generative AI was used in the preparation of this manuscript.

Ethical Approval and Consent to Participate

Not applicable.

References

Bohner, M., Stamov, G. T., & Stamova, I. M. (2020). Almost periodic solutions of Cohen–Grossberg neural networks with time-varying delay and variable impulsive perturbations. Communications in nonlinear science and numerical simulation, 80, 104952.
[CrossRef] [Google Scholar]
Huo, N., Li, B., & Li, Y. (2019). Existence and exponential stability of anti-periodic solutions for inertial quaternion-valued high-order Hopfield neural networks with state-dependent delays. IEEE Access, 7, 60010-60019.
[CrossRef] [Google Scholar]
Li, Y., & Xiang, J. (2020). Existence and global exponential stability of anti-periodic solutions for quaternion-valued cellular neural networks with time-varying delays. Advances in Difference Equations, 2020(1), 47.
[CrossRef] [Google Scholar]
Xiong, W. (2015). New result on convergence for HCNNs with time-varying leakage delays. Neural Computing and Applications, 26(2), 485-491.
[CrossRef] [Google Scholar]
Xu, C. J., & Li, P. L. (2017). New stability criteria for high-order neural networks with proportional delays. Communications in Theoretical Physics, 67(3), 235.
[CrossRef] [Google Scholar]
Li, Y., Wang, H., & Meng, X. (2019). Almost automorphic synchronization of quaternion-valued high-order Hopfield neural networks with time-varying and distributed delays. IMA Journal of Mathematical Control and Information, 36(3), 983-1013.
[CrossRef] [Google Scholar]
Li, Y., & Xiang, J. (2019). Existence and global exponential stability of anti-periodic solution for Clifford-valued inertial Cohen–Grossberg neural networks with delays. Neurocomputing, 332, 259-269.
[CrossRef] [Google Scholar]
Shen, W., Zhang, X., & Wang, Y. (2020). Stability analysis of high order neural networks with proportional delays. Neurocomputing, 372, 33-39.
[CrossRef] [Google Scholar]
Li, Y., & Xiang, J. (2019). Global asymptotic almost periodic synchronization of Clifford‐valued CNNs with discrete delays. Complexity, 2019(1), 6982109.
[CrossRef] [Google Scholar]
Aouiti, C., M’hamdi, M. S., & Chérif, F. (2017). New results for impulsive recurrent neural networks with time-varying coefficients and mixed delays. Neural Processing Letters, 46(2), 487-506.
[CrossRef] [Google Scholar]
Aouiti, C., & Dridi, F. (2019). Piecewise asymptotically almost automorphic solutions for impulsive non-autonomous high-order Hopfield neural networks with mixed delays. Neural Computing and Applications, 31(9), 5527-5545.
[CrossRef] [Google Scholar]
Brahmi, H., Ammar, B., Alimi, A. M., & Chérif, F. (2016, July). Pseudo almost periodic solutions of impulsive recurrent neural networks with mixed delays. In 2016 international joint conference on neural networks (IJCNN) (pp. 464-470). IEEE.
[CrossRef] [Google Scholar]
Blot, J., Mophou, G. M., N’guérékata, G. M., & Pennequin, D. (2009). Weighted pseudo almost automorphic functions and applications to abstract differential equations. Nonlinear Analysis: Theory, Methods & Applications, 71(3-4), 903-909.
[CrossRef] [Google Scholar]
Diagana, T. (2013). Almost automorphic type and almost periodic type functions in abstract spaces.
[CrossRef] [Google Scholar]
Dong, Y., Zhao, J., Miao, X., & Kang, M. (2023). Piecewise pseudo almost periodic solutions of interval general BAM neural networks with mixed time-varying delays and impulsive perturbations. AIMS Mathematics, 8(9), 21828-21855.
[CrossRef] [Google Scholar]
Li, Y., Xiang, J., & Li, B. (2019). Globally asymptotic almost automorphic synchronization of Clifford-valued RNNs with delays. IEEE Access, 7, 54946-54957.
[CrossRef] [Google Scholar]
Huo, N., & Li, Y. (2024). B‐almost periodic solutions in finite‐dimensional distributions for octonion‐valued stochastic shunting inhibitory cellular neural networks. Mathematical Methods in the Applied Sciences, 47(6), 5136-5160.
[CrossRef] [Google Scholar]
Wang, C., & Agarwal, R. P. (2014). Weighted piecewise pseudo almost automorphic functions with applications to abstract impulsive$\delta$-dynamic equations on time scales. Advances in Difference Equations, 2014(1), 153.
[CrossRef] [Google Scholar]
Zhu, J., & Sun, J. (2016). Global exponential stability of Clifford-valued recurrent neural networks. Neurocomputing, 173, 685-689.
[CrossRef] [Google Scholar]
Luo, D., & Qiu, Y. Anti-Periodic Solutions on Clifford-Valued High-Order Cohen--Grossberg Neural Networks with Multi-Proportional Delays. Available at SSRN 4710728. https://dx.doi.org/10.2139/ssrn.4710728
[Google Scholar]

Cite This Article

APA Style

Aouiti, C.& Dridi, F. (2025). Advances in the Mathematical Theory of WPAA Dynamics for Impulsive High Order Neural Systems in Clifford Algebras. Journal of Nonlinear Dynamics and Applications, 2(1), 1–12. https://doi.org/10.62762/JNDA.2025.838385

Export Citation

RIS Format

Compatible with EndNote, Zotero, Mendeley, and other reference managers

RIS format data for reference managers

TY  - JOUR
AU  - Aouiti, Chaouki
AU  - Dridi, Farah
PY  - 2026
DA  - 2026/01/21
TI  - Advances in the Mathematical Theory of WPAA Dynamics for Impulsive High Order Neural Systems in Clifford Algebras
JO  - Journal of Nonlinear Dynamics and Applications
T2  - Journal of Nonlinear Dynamics and Applications
JF  - Journal of Nonlinear Dynamics and Applications
VL  - 2
IS  - 1
SP  - 1
EP  - 12
DO  - 10.62762/JNDA.2025.838385
UR  - https://www.icck.org/article/abs/JNDA.2025.838385
KW  - impulsive systems
KW  - WPAA-functions
KW  - HOHNNs
KW  - Gronwall–Bellman inequality
KW  - exponential stability
KW  - clifford algebra
AB  - The primary objective of this work is to establish the existence, uniqueness, and exponential stability of piecewise weighted pseudo–almost automorphic solutions for impulsive high-order Hopfield neural networks formulated within Clifford algebras. Using the Banach fixed-point principle together with a suitably adapted Gronwall–Bellman inequality, we derive novel and verifiable sufficient conditions that ensure these qualitative properties. The main contributions are as follows: (i) this study is the first to analyze weighted pseudo–almost automorphic (WPAA) dynamics for impulsive high-order Hopfield neural networks directly in the Clifford algebra setting, without reducing the model to real-valued components; (ii) it offers a unified framework that accommodates both first- and second-order synaptic interactions under impulsive perturbations and mixed delays; and (iii) the resulting conditions explicitly capture the geometric structure of Clifford-valued states, providing a broader and algebraically consistent formulation compared to real or quaternion-valued models. The theoretical findings are further supported by a numerical example demonstrating their applicability and effectiveness.
SN  - 3069-6313
PB  - Institute of Central Computation and Knowledge
LA  - English
ER  -

BibTeX Format

Compatible with LaTeX, BibTeX, and other reference managers

BibTeX format data for LaTeX and reference managers

@article{Aouiti2026Advances,
  author = {Chaouki Aouiti and Farah Dridi},
  title = {Advances in the Mathematical Theory of WPAA Dynamics for Impulsive High Order Neural Systems in Clifford Algebras},
  journal = {Journal of Nonlinear Dynamics and Applications},
  year = {2026},
  volume = {2},
  number = {1},
  pages = {1-12},
  doi = {10.62762/JNDA.2025.838385},
  url = {https://www.icck.org/article/abs/JNDA.2025.838385},
  abstract = {The primary objective of this work is to establish the existence, uniqueness, and exponential stability of piecewise weighted pseudo–almost automorphic solutions for impulsive high-order Hopfield neural networks formulated within Clifford algebras. Using the Banach fixed-point principle together with a suitably adapted Gronwall–Bellman inequality, we derive novel and verifiable sufficient conditions that ensure these qualitative properties. The main contributions are as follows: (i) this study is the first to analyze weighted pseudo–almost automorphic (WPAA) dynamics for impulsive high-order Hopfield neural networks directly in the Clifford algebra setting, without reducing the model to real-valued components; (ii) it offers a unified framework that accommodates both first- and second-order synaptic interactions under impulsive perturbations and mixed delays; and (iii) the resulting conditions explicitly capture the geometric structure of Clifford-valued states, providing a broader and algebraically consistent formulation compared to real or quaternion-valued models. The theoretical findings are further supported by a numerical example demonstrating their applicability and effectiveness.},
  keywords = {impulsive systems, WPAA-functions, HOHNNs, Gronwall–Bellman inequality, exponential stability, clifford algebra},
  issn = {3069-6313},
  publisher = {Institute of Central Computation and Knowledge}
}

Article Metrics

Citations:

Google Scholar

Crossref

Scopus

Web of Science

Article Access Statistics:

PDF Downloads: 32

Publisher's Note

ICCK stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and Permissions

Institute of Central Computation and Knowledge (ICCK) or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Journal of Nonlinear Dynamics and Applications

ISSN: 3069-6313 (Online)

Email: [email protected]

Portico

All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/

User

Unlimited Downloads

Complete Library Access

Membership Eligibility

Community Leadership Opportunities

Google Scholar

Crossref

Scopus

Web of Science