Analytical Kinematic Modeling and Simulation Verification of a Three-Link Planar Manipulator

Nuoyu Jiang

doi:10.62762/TICPS.2026.746937

Volume 1, Issue 1, ICCK Transactions on Intelligent Cyber-Physical Systems

Volume 1, Issue 1, 2025

Submit Manuscript Edit a Special Issue

Article QR Code

Scan the QR code for reading

Popular articles

Case Studies on Integrating Artificial Intelligence in Finance to Transform Decision Making and Risk Management for Enhanced Financial Outcomes Reservoir Science: A Multi-Coupling Communication Platform to Promote Energy Transformation, Climate Change and Environmental Protection Reinforcement Learning for Prompt Optimization in Language Models: A Comprehensive Survey of Methods, Representations, and Evaluation Challenges AI and the Future of Education: Advancing Personalized Learning and Intelligent Tutoring Systems From CO$_2$ Sequestration to Hydrogen Storage: Further Utilization of Depleted Gas Reservoirs Effects of Crosslinking Agents and Reservoir Conditions on the Propagation of Fractures in Coal Reservoirs During Hydraulic Fracturing The Influence of Geological Factors and Transmission Fluids on the Exploitation of Reservoir Geothermal Resources: Factor Discussion and Mechanism Analysis Plant Disease Detection Using Deep Learning Techniques Modeling Brain Functional Networks Using Graph Neural Networks: A Review and Clinical Application YOLOv8-Lite: A Lightweight Object Detection Model for Real-time Autonomous Driving Systems

ICCK Transactions on Intelligent Cyber-Physical Systems, Volume 1, Issue 1, 2025: 26-37

Free to Read | Research Article | 13 February 2026

Analytical Kinematic Modeling and Simulation Verification of a Three-Link Planar Manipulator

Nuoyu Jiang 1 *

1 School of Electrical Engineering, Yancheng Institute of Technology, Yancheng 224051, China

* Corresponding Author: Nuoyu Jiang, [email protected]

DOI: 10.62762/TICPS.2026.746937

ARK: ark:/57805/ticps.2026.746937

Received: 06 January 2026, Accepted: 03 February 2026, Published: 13 February 2026

PDF (1.55 MB)

Article Metrics Cite This Article

Abstract

This paper establishes an analytical kinematic model for a three-degree-of-freedom planar manipulator with three serial links, and validates it through MATLAB numerical simulations and SolidWorks-ADAMS co-simulation. Based on the mechanism topology and the Denavit-Hartenberg (D-H) parameter method, coordinate frames are assigned, and homogeneous transformation modeling is performed, leading to a closed-form forward kinematics expression for the end-effector pose. By combining wrist-point decomposition, geometric approaches, and the law of cosines, an analytical inverse kinematics solution is derived, and the characteristics of multiple solution configurations are discussed. The simulation results show that the analytical forward and inverse kinematics are consistent with the numerical outputs from the Robotics Toolbox, and the inverse solution can reliably recover the joint angles. In the ADAMS simulation, joint responses follow a sinusoidal driving law, and the end-effector trajectory is continuous and smooth, satisfying the motion characteristics of planar mechanisms. These results confirm the correctness and engineering applicability of the proposed model.

Graphical Abstract

Keywords

three-link planar manipulator

D-H parameter method

forward kinematics

analytical inverse kinematics

MATLAB and ADAMS simulation validation

Data Availability Statement

Data will be made available on request.

Funding

This work was supported without any funding.

Conflicts of Interest

The author declares no conflicts of interest.

AI Use Statement

The author declares that no generative AI was used in the preparation of this manuscript.

Ethical Approval and Consent to Participate

Not applicable.

References

Craig, J. J. (2009). Introduction to robotics: mechanics and control, 3/E. Pearson Education India.
[Google Scholar]
Bartoš, M., Bulej, V., Bohušík, M., Stanček, J., Ivanov, V., & Macek, P. (2021). An overview of robot applications in automotive industry. Transportation Research Procedia, 55, 837–844.
[CrossRef] [Google Scholar]
Siciliano, B., Khatib, O., & Kröger, T. (Eds.). (2008). Springer handbook of robotics (Vol. 200, p. 1). Berlin: springer.
[CrossRef] [Google Scholar]
Corke, P. I., Jachimczyk, W., & Pillat, R. (2011). Robotics, vision and control: fundamental algorithms in MATLAB (Vol. 73, p. 2). Berlin: Springer.
[CrossRef] [Google Scholar]
Spong, M. W., Hutchinson, S., & Vidyasagar, M. (2020). Robot modeling and control. John Wiley & amp.
[CrossRef] [Google Scholar]
Lynch, K. M., & Park, F. C. (2017). Modern Robotics: Mechanics, Planning, and Control. Cambridge University Press.
[CrossRef] [Google Scholar]
Angeles, J. (Ed.). (2003). Fundamentals of robotic mechanical systems: theory, methods, and algorithms. New York, NY: Springer New York.
[CrossRef] [Google Scholar]
Khalil, W., & Dombre, E. (2002). Modeling, Identification and Control of Robots. Butterworth-Heinemann.
[Google Scholar]
Kucuk, S., & Bingul, Z. (2006). Robot Kinematics: Forward and Inverse Kinematics. In Industrial Robotics: Theory, Modelling and Control. IntechOpen.
[CrossRef] [Google Scholar]
Urrea, C., & Kern, J. (2025). Recent Advances and Challenges in Industrial Robotics: A Systematic Review of Technological Trends and Emerging Applications. Processes, 13(3), 832.
[CrossRef] [Google Scholar]
Paul, R. P. (1981). Robot Manipulators: Mathematics, Programming, and Control. MIT Press.
[Google Scholar]
Waseem, S., Adnan, M., Iqbal, M. S., Amin, A. A., Shah, A., & Tariq, M. (2025). From classical to intelligent control: Evolving trends in robotic manipulator technology. Computers and Electrical Engineering, 127, 110559.
[CrossRef] [Google Scholar]
Pieper, D. L. (1969). The kinematics of manipulators under computer control. Stanford University.
[Google Scholar]
Featherstone, R. (2008). Rigid Body Dynamics Algorithms. Springer.
[CrossRef] [Google Scholar]
Tinoco, V., Silva, M. F., Santos, F. N., Morais, R., Magalhães, S. A., & Oliveira, P. M. (2025). A review of advanced controller methodologies for robotic manipulators. International Journal of Dynamics and Control, 13(1), 36.
[CrossRef] [Google Scholar]
Tsai, L. W. (1999). Robot analysis: the mechanics of serial and parallel manipulators. John Wiley & Sons.
[Google Scholar]
Selig, J. M. (2005). Geometric fundamentals of robotics. New York, NY: Springer New York.
[CrossRef] [Google Scholar]
Zhang, W., Chen, R., Chen, H., You, Z., & Zhao, Y. (2025). Research on a New Pre-defined Time Sliding Mode Control Method for Nonlinear Systems. IAENG International Journal of Applied Mathematics, 55(8), 2482–2488.
[Google Scholar]
Manocha, D., & Canny, J. F. (1994). Efficient inverse kinematics for general 6R manipulators. IEEE Transactions on Robotics and Automation, 10(5), 648–657.
[CrossRef] [Google Scholar]
Jazar, R. N. (2010). Theory of Applied Robotics: Kinematics, Dynamics, and Control (2nd ed.). Springer.
[CrossRef] [Google Scholar]
Merlet, J. P. (2006). Parallel robots. Dordrecht: Springer Netherlands.
[CrossRef] [Google Scholar]
Sciavicco, L., & Siciliano, B. (2012). Modelling and Control of Robot Manipulators (2nd ed.). Springer.
[CrossRef] [Google Scholar]
Murray, R. M., Li, Z., & Sastry, S. S. (1994). A Mathematical Introduction to Robotic Manipulation. CRC Press.
[CrossRef] [Google Scholar]
Siciliano, B., & Khatib, O. (2016). Robotics and the handbook. In Springer Handbook of Robotics (pp. 1-6). Cham: Springer International Publishing.
[CrossRef] [Google Scholar]
Mason, M. T. (2001). Mechanics of Robotic Manipulation. MIT Press.
[CrossRef] [Google Scholar]
Ghosal, A. (2006). Robotics: Fundamental Concepts and Analysis. Oxford University Press.
[Google Scholar]
Sharkawy, A. N., & Khairullah, S. S. (2023). Forward and Inverse Kinematics Solution of A 3-DOF Articulated Robotic Manipulator Using Artificial Neural Network. International Journal of Robotics & Control Systems, 3(2), 340–357. http://dx.doi.org/10.31763/ijrcs.v3i2.1017
[Google Scholar]
Zaplana, I., Hadfield, H., & Lasenby, J. (2022). Closed-form solutions for the inverse kinematics of serial robots using conformal geometric algebra. Mechanism and Machine Theory, 173, 104835.
[CrossRef] [Google Scholar]
Denavit, J., & Hartenberg, R. S. (1955). A kinematic notation for lower-pair mechanisms based on matrices. Journal of Applied Mechanics, 22(2), 215–221.
[CrossRef] [Google Scholar]
Kucuk, S., & Bingul, Z. (2014). Inverse kinematics solutions for industrial robot manipulators with offset wrists. Applied Mathematical Modelling, 38(7–8), 1983–1999.
[CrossRef] [Google Scholar]

Cite This Article

APA Style

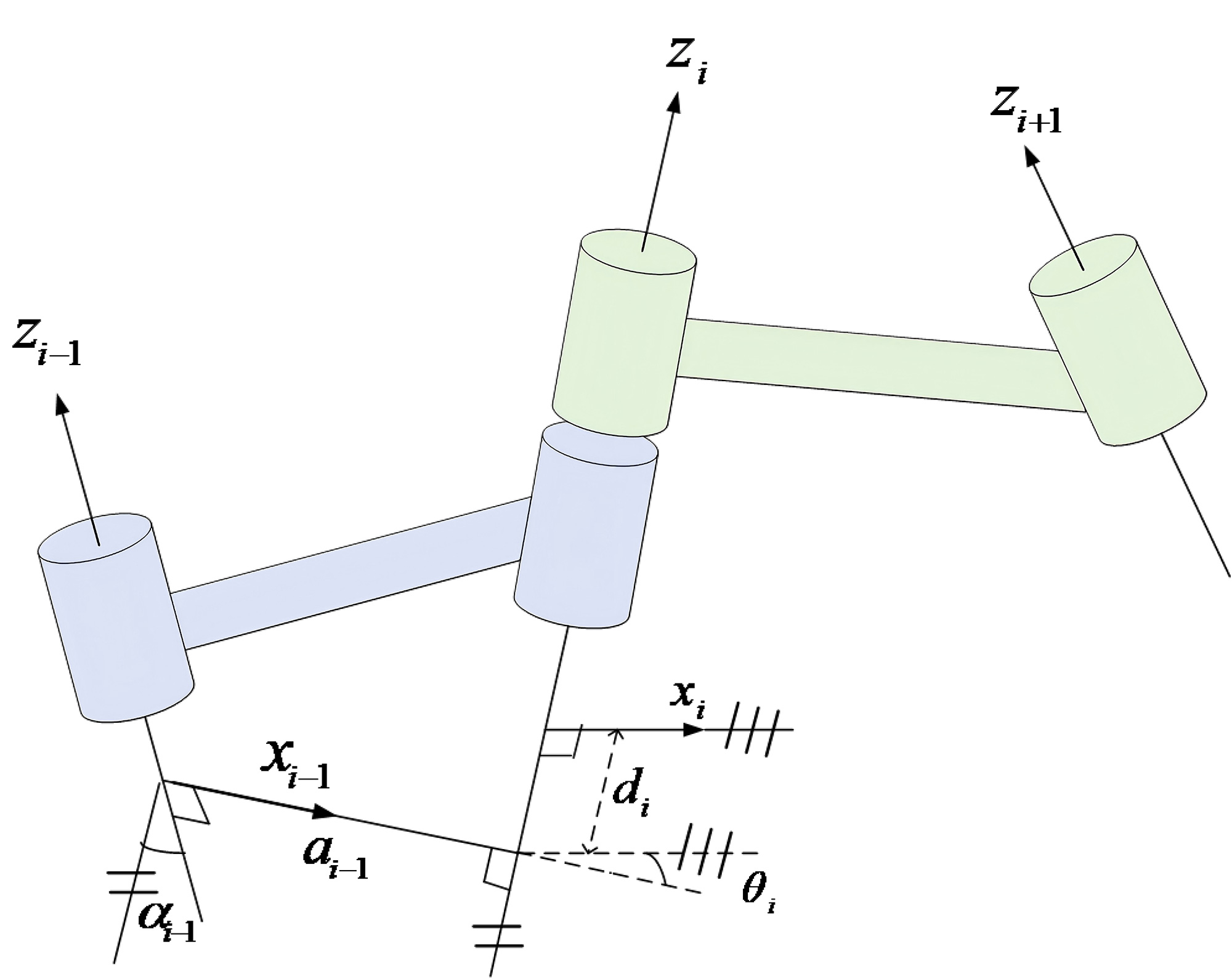
Jiang, N. (2026). Analytical Kinematic Modeling and Simulation Verification of a Three-Link Planar Manipulator. ICCK Transactions on Intelligent Cyber-Physical Systems, 1(1), 26–37. https://doi.org/10.62762/TICPS.2026.746937

Export Citation

RIS Format

Compatible with EndNote, Zotero, Mendeley, and other reference managers

RIS format data for reference managers

TY  - JOUR
AU  - Jiang, Nuoyu
PY  - 2026
DA  - 2026/02/13
TI  - Analytical Kinematic Modeling and Simulation Verification of a Three-Link Planar Manipulator
JO  - ICCK Transactions on Intelligent Cyber-Physical Systems
T2  - ICCK Transactions on Intelligent Cyber-Physical Systems
JF  - ICCK Transactions on Intelligent Cyber-Physical Systems
VL  - 1
IS  - 1
SP  - 26
EP  - 37
DO  - 10.62762/TICPS.2026.746937
UR  - https://www.icck.org/article/abs/TICPS.2026.746937
KW  - three-link planar manipulator
KW  - D-H parameter method
KW  - forward kinematics
KW  - analytical inverse kinematics
KW  - MATLAB and ADAMS simulation validation
AB  - This paper establishes an analytical kinematic model for a three-degree-of-freedom planar manipulator with three serial links, and validates it through MATLAB numerical simulations and SolidWorks-ADAMS co-simulation. Based on the mechanism topology and the Denavit-Hartenberg (D-H) parameter method, coordinate frames are assigned, and homogeneous transformation modeling is performed, leading to a closed-form forward kinematics expression for the end-effector pose. By combining wrist-point decomposition, geometric approaches, and the law of cosines, an analytical inverse kinematics solution is derived, and the characteristics of multiple solution configurations are discussed. The simulation results show that the analytical forward and inverse kinematics are consistent with the numerical outputs from the Robotics Toolbox, and the inverse solution can reliably recover the joint angles. In the ADAMS simulation, joint responses follow a sinusoidal driving law, and the end-effector trajectory is continuous and smooth, satisfying the motion characteristics of planar mechanisms. These results confirm the correctness and engineering applicability of the proposed model.
SN  - pending
PB  - Institute of Central Computation and Knowledge
LA  - English
ER  -

BibTeX Format

Compatible with LaTeX, BibTeX, and other reference managers

BibTeX format data for LaTeX and reference managers

@article{Jiang2026Analytical,
  author = {Nuoyu Jiang},
  title = {Analytical Kinematic Modeling and Simulation Verification of a Three-Link Planar Manipulator},
  journal = {ICCK Transactions on Intelligent Cyber-Physical Systems},
  year = {2026},
  volume = {1},
  number = {1},
  pages = {26-37},
  doi = {10.62762/TICPS.2026.746937},
  url = {https://www.icck.org/article/abs/TICPS.2026.746937},
  abstract = {This paper establishes an analytical kinematic model for a three-degree-of-freedom planar manipulator with three serial links, and validates it through MATLAB numerical simulations and SolidWorks-ADAMS co-simulation. Based on the mechanism topology and the Denavit-Hartenberg (D-H) parameter method, coordinate frames are assigned, and homogeneous transformation modeling is performed, leading to a closed-form forward kinematics expression for the end-effector pose. By combining wrist-point decomposition, geometric approaches, and the law of cosines, an analytical inverse kinematics solution is derived, and the characteristics of multiple solution configurations are discussed. The simulation results show that the analytical forward and inverse kinematics are consistent with the numerical outputs from the Robotics Toolbox, and the inverse solution can reliably recover the joint angles. In the ADAMS simulation, joint responses follow a sinusoidal driving law, and the end-effector trajectory is continuous and smooth, satisfying the motion characteristics of planar mechanisms. These results confirm the correctness and engineering applicability of the proposed model.},
  keywords = {three-link planar manipulator, D-H parameter method, forward kinematics, analytical inverse kinematics, MATLAB and ADAMS simulation validation},
  issn = {pending},
  publisher = {Institute of Central Computation and Knowledge}
}

Article Metrics

Citations:

Google Scholar

Crossref

Scopus

Web of Science

Article Access Statistics:

PDF Downloads: 5

Publisher's Note

ICCK stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and Permissions

Institute of Central Computation and Knowledge (ICCK) or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

ICCK Transactions on Intelligent Cyber-Physical Systems

ISSN: pending (Online)

Email: [email protected]

Portico

All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/

User

Unlimited Downloads

Complete Library Access

Membership Eligibility

Community Leadership Opportunities

Google Scholar

Crossref

Scopus

Web of Science