International Journal of Thermo-Fluid Systems and Sustainable Energy Home About Editors Current Issue
  1. Home
  2. Journals
  3. International Journal of Thermo-Fluid Systems and Sustainable Energy
  4. Volume 1, Issue 2
Thermal and Chemical Dynamics in Magnetohydrodynamic Williamson Fluid Flow over a Stretching Cylinder under Heat/Mass Flux Effects Using Optimal Homotopy Analysis Method
Research Article | Published: 22 November 2025
International Journal of Thermo-Fluid Systems and Sustainable Energy Volume 1, Issue 2, 2025: 46-63
Volume 1, Issue 2, International Journal of Thermo-Fluid Systems and Sustainable Energy
Volume 1, Issue 2, 2025
Submit Manuscript Edit a Special Issue
Article QR Code
Article QR Code
Scan the QR code for reading
Popular articles
Case Studies on Integrating Artificial Intelligence in Finance to Transform Decision Making and Risk Management for Enhanced Financial Outcomes Reservoir Science: A Multi-Coupling Communication Platform to Promote Energy Transformation, Climate Change and Environmental Protection Reinforcement Learning for Prompt Optimization in Language Models: A Comprehensive Survey of Methods, Representations, and Evaluation Challenges From CO$_2$ Sequestration to Hydrogen Storage: Further Utilization of Depleted Gas Reservoirs AI and the Future of Education: Advancing Personalized Learning and Intelligent Tutoring Systems Effects of Crosslinking Agents and Reservoir Conditions on the Propagation of Fractures in Coal Reservoirs During Hydraulic Fracturing The Influence of Geological Factors and Transmission Fluids on the Exploitation of Reservoir Geothermal Resources: Factor Discussion and Mechanism Analysis YOLOv8-Lite: A Lightweight Object Detection Model for Real-time Autonomous Driving Systems Plant Disease Detection Using Deep Learning Techniques Modeling Brain Functional Networks Using Graph Neural Networks: A Review and Clinical Application
International Journal of Thermo-Fluid Systems and Sustainable Energy, Volume 1, Issue 2, 2025: 46-63

Open Access | Research Article | 22 November 2025
Thermal and Chemical Dynamics in Magnetohydrodynamic Williamson Fluid Flow over a Stretching Cylinder under Heat/Mass Flux Effects Using Optimal Homotopy Analysis Method
by
Nimra Riaz Nimra Riaz 1
Muhammad Sohail Muhammad Sohail 1 *
1 Institute of Mathematics, Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan 64200, Pakistan
* Corresponding Author: Muhammad Sohail, [email protected]
DOI: 10.62762/IJTSSE.2025.383195
ARK: ark:/57805/ijtsse.2025.383195
Received: 19 July 2025, Accepted: 30 August 2025, Published: 22 November 2025  
   PDF  (2.62 MB)
Article Metrics Cite This Article
Abstract
The knowledge on understanding non-Newtonian fluid dynamics influences and behaviors in magnetic and nanoscale effects of transport is also important to the advanced processes of engineering. The current paper examines MHD flow and heat transfer of a Williamson nanofluid across a stretching cylindrical surface, taking into consideration Hall current and chemical reaction and non-Fourier heat and mass flux that is described by the Cattaneo Christov theory. The transport of Nanoparticles is explained in terms of Buongiorno model of thermophoresis and Brownian movement. Similarity variables are used to transform the governing nonlinear equations and then analytically solved via Optimal Homotopy Analysis Method. The parametric study of parameters like $M = 0.5 - 2.0$, $\gamma = 0.1 - 5.0$, $Nt = 0.1 - 0.5$, $Nb = 0.1 - 0.3$, $\delta t = \delta c = 0.1 - 0.5$, and $Kr = 0.1 - 1.0$ indicates that the values of the magnetic field, relaxation times, Hall currents, and diffusion of nanoparticles have a considerable effect on the flow, thermal, and concentration fields. The results have interesting applications in polymer extrusion, thermal control of nano-devices, magnetic drug delivery, and manufacturing smart materials.
Graphical Abstract
Thermal and Chemical Dynamics in Magnetohydrodynamic Williamson Fluid Flow over a Stretching Cylinder under Heat/Mass Flux Effects Using Optimal Homotopy Analysis Method
Keywords
williamson fluid
Magnetohydrodynamics (MHD)
hall effect
buongiorno model
cattaneo-christov flux
chemical reaction
nanofluid
stretched cylinder
optimal homotopy analysis method
Data Availability Statement
Data will be made available on request.
Funding
This work was supported without any funding.
Conflicts of Interest
The authors declare no conflicts of interest.
Ethical Approval and Consent to Participate
Not applicable.
References
  1. Das, S. K., Choi, S. U., Yu, W., & Pradeep, T. (2007). Nanofluids: science and technology. John Wiley & Sons.
    [Google Scholar]
  2. Böhme, G. (2012). Non-Newtonian fluid mechanics (Vol. 31). Elsevier.
    [Google Scholar]
  3. Makkar, V., Poply, V., & Sharma, N. (2023). Three dimensional modelling of magnetohydrodynamic bio-convective Casson nanofluid flow with buoyancy effects over exponential stretching sheet along with heat source & gyrotactic micro-organisms. Journal of Nanofluids, 12(2), 535-547.
    [CrossRef]   [Google Scholar]
  4. Turkyilmazoglu, M., & Pop, I. (2024). Flow and heat transfer in annuli owing to inner shrinking and outer stationary cylinder. Chinese Journal of Physics, 89, 1899-1907.
    [CrossRef]   [Google Scholar]
  5. Hamid, A., Muhammad, T., & Irfan, M. (2024). Diffusions of nanoparticles and existence of multiple solutions for MHD Williamson nanofluid with slip mechanism. Scientia Iranica.
    [CrossRef]   [Google Scholar]
  6. Harfouf, A. E., Mounir, S. H., Mejdal, M., Mes-Adi, H., Herbazi, R., Rasool, G., ... & Nfaoui, M. (2024, October). Analysis of Magnetohydrodynamics Williamson Fluid’s Thermal Radiation and Ohmic Heating Effects via an Inclined Channel. In International Conference Interdisciplinarity in Engineering (pp. 382-401). Cham: Springer Nature Switzerland.
    [CrossRef]   [Google Scholar]
  7. Khan, S. U., Riaz, A., & Ramesh, K. (2025). ACCELERATING BIOCONVECTIVE FLOW OF MICROPOLAR NANOFLUID DUE TO POROUS OSCILLATORY SURFACE WITH NONLINEAR THERMAL RADIATION, VISCOUS DISSIPATION AND SUCTION EFFECTS. Journal of Porous Media, 28.
    [CrossRef]   [Google Scholar]
  8. Ramzan, M., Bilal, M., & Chung, J. D. (2017). Radiative Williamson nanofluid flow over a convectively heated Riga plate with chemical reaction-A numerical approach. Chinese Journal of Physics, 55(4), 1663-1673.
    [CrossRef]   [Google Scholar]
  9. Nadeem, S., Ishtiaq, B., Alzabut, J., & Ghazwani, H. A. (2024). Entropy generation for exact irreversibility analysis in the MHD channel flow of Williamson fluid with combined convective-radiative boundary conditions. Heliyon, 10(4).
    [CrossRef]   [Google Scholar]
  10. Ahmad, S., Ahammad, N. A., Khan, M. N., Algehyne, E. A., Tag-Eldin, E., Gepreel, K. A., ... & Galal, A. M. (2022). Thermal and solutal energy transport analysis in entropy generation of hybrid nanofluid flow over a vertically rotating cylinder. Frontiers in Physics, 10, 988407.
    [CrossRef]   [Google Scholar]
  11. Turkyilmazoglu, M. (2021). Exact solutions concerning momentum and thermal fields induced by a long circular cylinder. The European Physical Journal Plus, 136(5), 1-10.
    [CrossRef]   [Google Scholar]
  12. Shah, Z., Alzahrani, E. O., Alghamdi, W., & Ullah, M. Z. (2020). Influences of electrical MHD and Hall current on squeezing nanofluid flow inside rotating porous plates with viscous and joule dissipation effects. Journal of Thermal Analysis and Calorimetry, 140(3), 1215-1227.
    [CrossRef]   [Google Scholar]
  13. Turkyilmazoglu, M. (2024). Evidence of stretching/moving sheet-triggered nonlinear similarity flows: atomization and electrospinning with/without air resistance. International Journal of Numerical Methods for Heat & Fluid Flow, 34(9), 3598-3614.
    [CrossRef]   [Google Scholar]
  14. Cattaneo, C. (1948). Sulla conduzione del calore. Atti Sem. Mat. Fis. Univ. Modena, 3, 83-101.
    [CrossRef]   [Google Scholar]
  15. Ván, P., & Fülöp, T. (2012). Universality in heat conduction theory: weakly nonlocal thermodynamics. Annalen der Physik, 524(8), 470-478.
    [CrossRef]   [Google Scholar]
  16. Ali, A., Khatoon, R., Ashraf, M., & Awais, M. (2022). Cattaneo–Christov heat flux on MHD flow of hybrid nanofluid across stretched cylinder with radiations and Joule heating effects. Waves in Random and Complex Media, 1-18.
    [CrossRef]   [Google Scholar]
  17. Khan, M., Shahid, A., Salahuddin, T., Malik, M. Y., & Hussain, A. (2020). Analysis of two dimensional Carreau fluid flow due to normal surface condition: A generalized Fourier’s and Fick’s laws. Physica A: Statistical Mechanics and its Applications, 540, 123024.
    [CrossRef]   [Google Scholar]
  18. Sohail, M., & Nazir, U. (2023). Numerical computation of thermal and mass transportation in Williamson material utilizing modified fluxes via optimal homotopy analysis procedure. Waves in Random and Complex Media, 1-22.
    [CrossRef]   [Google Scholar]
  19. Nadeem, S., Ahmad, S., & Muhammad, N. (2017). Cattaneo-Christov flux in the flow of a viscoelastic fluid in the presence of Newtonian heating. Journal of Molecular liquids, 237, 180-184.
    [CrossRef]   [Google Scholar]
  20. Li, X., Abbasi, A., Al-Khaled, K., Ameen, H. F. M., Khan, S. U., Khan, M. I., ... & Guedri, K. (2023). Thermal performance of iron oxide and copper (Fe3O4, Cu) in hybrid nanofluid flow of Casson material with Hall current via complex wavy channel. Materials Science and Engineering: B, 289, 116250.
    [CrossRef]   [Google Scholar]
  21. Shafiq, A., Khan, I., Rasool, G., Seikh, A. H., & Sherif, E. S. M. (2019). Significance of double stratification in stagnation point flow of third-grade fluid towards a radiative stretching cylinder. Mathematics, 7(11), 1103.
    [CrossRef]   [Google Scholar]
  22. Khan, M. N., Alhuthali, A. M., Amjad, A., Saqlain, M., Yar, M., Alshammry, N., & Elkotb, M. A. (2024). Numerical investigation of mixed convective flow of micropolar Casson fluid with Cattaneo–Christov heat flux model on an inclined vertical stretching surface. Journal of Computational Design and Engineering, 11(3), 174-184.
    [CrossRef]   [Google Scholar]
  23. Ali, F., Padmavathi, T., & Hemalatha, B. (2025). Entropy minimization in Darcy Forchheimer on Sutterby nanofluid past a stretching surface with swimming of gyrotactic microorganisms. Waves in Random and Complex Media, 35(5), 10333-10356.
    [CrossRef]   [Google Scholar]
  24. Khan, N. S., Gul, T., Islam, S., Khan, A., & Shah, Z. (2017). Brownian motion and thermophoresis effects on MHD mixed convective thin film second-grade nanofluid flow with Hall effect and heat transfer past a stretching sheet. Journal of Nanofluids, 6(5), 812-829.
    [CrossRef]   [Google Scholar]
  25. Sohail, M., Rafique, E., & Abodayeh, K. (2024). Boundary layer analysis on magnetohydrodynamic dissipative Williamson nanofluid past over an exponentially stretched porous sheet by engaging OHAM. Multidiscipline Modeling in Materials and Structures, 20(6), 973-994.
    [CrossRef]   [Google Scholar]
  26. Hussain Shah, S. Z., Ayub, A., Khan, U., Darvesh, A., Sherif, E. S. M., & Pop, I. (2024). Thermal transport exploration of ternary hybrid nanofluid flow in a non-Newtonian model with homogeneous-heterogeneous chemical reactions induced by vertical cylinder. Advances in mechanical engineering, 16(5), 16878132241252229.
    [CrossRef]   [Google Scholar]
  27. Abbas, Z., Naveed, M., & Sajid, M. (2013). Heat transfer analysis for stretching flow over a curved surface with magnetic field. Journal of Engineering Thermophysics, 22(4), 337-345.
    [CrossRef]   [Google Scholar]
  28. Zaman, S. U., Aslam, M. N., Riaz, M. B., Akgul, A., & Hussan, A. (2024). Williamson MHD nanofluid flow with radiation effects through slender cylinder. Results in Engineering, 22, 101966.
    [CrossRef]   [Google Scholar]
  29. Rauf, A., Faisal, Shah, N. A., & Botmart, T. (2022). Hall current and morphological effects on MHD micropolar non-Newtonian tri-hybrid nanofluid flow between two parallel surfaces. Scientific Reports, 12(1), 16608.
    [CrossRef]   [Google Scholar]
  30. Rasheed, H. U., Khan, Z., El-Zahar, E. R., Shah, N. A., Islam, S., & Abbas, T. (2025). Homotopic solutions of an unsteady magnetohydrodynamic flow of Casson nanofluid flow by a vertical cylinder with Brownian and viscous dissipation effects. Waves in Random and Complex Media, 35(5), 9457-9470.
    [CrossRef]   [Google Scholar]
  31. Krishna, M. V., Bharathi, K., & Chamkha, A. J. (2018). Hall effects on MHD peristaltic flow of Jeffrey fluid through porous medium in a vertical stratum. Interfacial Phenomena and Heat Transfer, 6(3).
    [CrossRef]   [Google Scholar]
  32. Elsaid, E. M., Abd El-Aziz, M., Aly, A. M., Alruwaili, A. S., & Eid, M. R. (2024). Physical analysis and thermal case of magnetized fluid flow and heat transfer via stretchable cylinder: Hall impact and entropy generation. Modern Physics Letters B, 38(36), 2450371.
    [CrossRef]   [Google Scholar]
  33. Gul, T., Khan, A. S., Islam, S., Alqahtani, A. M., Khan, I., Alshomrani, A. S., ... & Muradullah. (2017). Heat transfer investigation of the unsteady thin film flow of Williamson fluid past an inclined and oscillating moving plate. Applied Sciences, 7(4), 369.
    [CrossRef]   [Google Scholar]
  34. Khan, W., Gul, T., Idrees, M., Islam, S., Khan, I., & Dennis, L. C. C. (2016). Thin film Williamson nanofluid flow with varying viscosity and thermal conductivity on a time-dependent stretching sheet. Applied Sciences, 6(11), 334.
    [CrossRef]   [Google Scholar]
  35. Awwad, F. A., Ismail, E. A., Khan, W., Gul, T., & Khan, A. S. (2023). Comparative numerical analysis for the error estimation of the fluid flow over an inclined axisymmetric cylinder with a gyrotactic microbe. Symmetry, 15(10), 1811.
    [CrossRef]   [Google Scholar]
  36. Gul, T., & Afridi, S. (2018). The heat and mass transfer analysis during bunch coating of a stretching cylinder by Casson fluid. In Fluid Flow Problems. IntechOpen.
    [CrossRef]   [Google Scholar]
  37. Nadeem, S., Hussain, S. T., & Lee, C. (2013). Flow of a Williamson fluid over a stretching sheet. Brazilian journal of chemical engineering, 30, 619-625.
    [CrossRef]   [Google Scholar]
  38. Malik, M. Y., Bibi, M., Khan, F., & Salahuddin, T. (2016). Numerical solution of Williamson fluid flow past a stretching cylinder and heat transfer with variable thermal conductivity and heat generation/absorption. AIP Advances, 6(3).
    [CrossRef]   [Google Scholar]
  39. Bilal, M., Sagheer, M., & Hussain, S. (2018). Numerical study of magnetohydrodynamics and thermal radiation on Williamson nanofluid flow over a stretching cylinder with variable thermal conductivity. Alexandria engineering journal, 57(4), 3281-3289.
    [CrossRef]   [Google Scholar]
  40. Jakhar, A., Sukariya, V. K., Kumar, S., Kumar, A., & Anurag. (2024). Study of MHD Williamson fluid flow over a stretched cylinder with Hall, thermal dynamics, and chemical reactions effects. Journal of Thermal Analysis and Calorimetry, 1-18.
    [CrossRef]   [Google Scholar]
  41. Sohail, M., Rafique, E., Mahariq, I., & Qureshi, I. H. (2024). Analytical investigation via OHAM on thermally magnetized non-Newtonian Williamson fluid with heat generation and thermal radiation effects. Proceedings of the Institution of Mechanical Engineers, Part N: Journal of Nanomaterials, Nanoengineering and Nanosystems, 23977914251338150.
    [CrossRef]   [Google Scholar]
  42. Omar, H. A. (2021). An integrated genetic algorithm and homotopy analysis method to solve nonlinear equation systems. Mathematical Problems in Engineering, 2021(1), 5589322.
    [CrossRef]   [Google Scholar]
  43. Pathak, S., & Singh, T. (2015). Optimal homotopy analysis methods for solving the linear and nonlinear fokker-planck equations. British Journal of Mathematics & Computer Science, SCIENCEDOMAIN international, 7(3), 209-217.
    [Google Scholar]
  44. Jasim, M., Anakira, N., Kamel, L., Amourah, A., Fareed, A., & Al Kalbani, K. S. (2024). Improved solutions of oham approximate procedure for classes of nonlinear odes. Contemporary Mathematics, 5(3), 4115.
    [CrossRef]   [Google Scholar]
  45. Anakira, N. R., Alomari, A. K., Jameel, A. F., & Hashim, I. (2017). Multistage optimal homotopy asymptotic method for solving boundary value problems with robin boundary conditions. Far East Journal of Mathematical Sciences, 102(8), 1727-1744. http://dx.doi.org/10.17654/MS102081727
    [Google Scholar]
  46. Bahia, G., Ouannas, A., Batiha, I. M., & Odibat, Z. (2021). The optimal homotopy analysis method applied on nonlinear time‐fractional hyperbolic partial differential equation s. Numerical Methods for Partial Differential Equations, 37(3), 2008-2022.
    [CrossRef]   [Google Scholar]
Cite This Article
APA Style
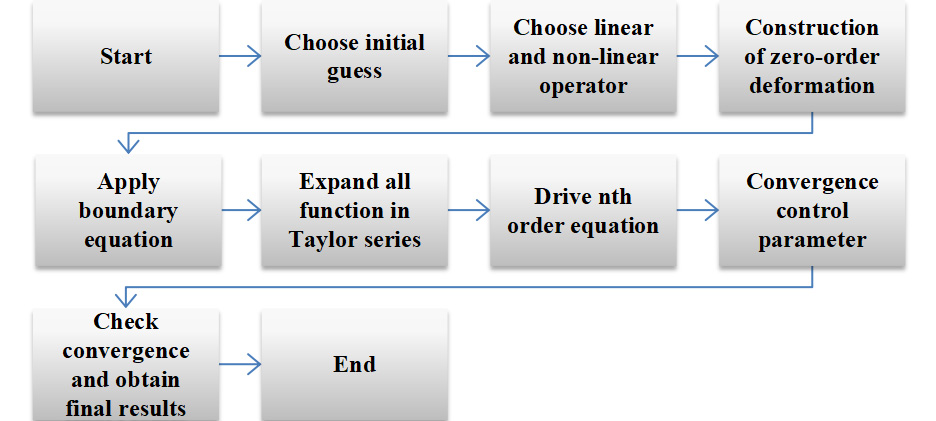
Riaz, N., & Sohail, M. (2025). Thermal and Chemical Dynamics in Magnetohydrodynamic Williamson Fluid Flow over a Stretching Cylinder under Heat/Mass Flux Effects Using Optimal Homotopy Analysis Method. International Journal of Thermo-Fluid Systems and Sustainable Energy, 1(2), 46–63. https://doi.org/10.62762/IJTSSE.2025.383195
Export Citation
RIS Format
Compatible with EndNote, Zotero, Mendeley, and other reference managers
RIS format data for reference managers
TY  - JOUR
AU  - Riaz, Nimra
AU  - Sohail, Muhammad
PY  - 2025
DA  - 2025/11/22
TI  - Thermal and Chemical Dynamics in Magnetohydrodynamic Williamson Fluid Flow over a Stretching Cylinder under Heat/Mass Flux Effects Using Optimal Homotopy Analysis Method
JO  - International Journal of Thermo-Fluid Systems and Sustainable Energy
T2  - International Journal of Thermo-Fluid Systems and Sustainable Energy
JF  - International Journal of Thermo-Fluid Systems and Sustainable Energy
VL  - 1
IS  - 2
SP  - 46
EP  - 63
DO  - 10.62762/IJTSSE.2025.383195
UR  - https://www.icck.org/article/abs/IJTSSE.2025.383195
KW  - williamson fluid
KW  - Magnetohydrodynamics (MHD)
KW  - hall effect
KW  - buongiorno model
KW  - cattaneo-christov flux
KW  - chemical reaction
KW  - nanofluid
KW  - stretched cylinder
KW  - optimal homotopy analysis method
AB  - The knowledge on understanding non-Newtonian fluid dynamics influences and behaviors in magnetic and nanoscale effects of transport is also important to the advanced processes of engineering. The current paper examines MHD flow and heat transfer of a Williamson nanofluid across a stretching cylindrical surface, taking into consideration Hall current and chemical reaction and non-Fourier heat and mass flux that is described by the Cattaneo Christov theory. The transport of Nanoparticles is explained in terms of Buongiorno model of thermophoresis and Brownian movement. Similarity variables are used to transform the governing nonlinear equations and then analytically solved via Optimal Homotopy Analysis Method. The parametric study of parameters like $M = 0.5 - 2.0$, $\gamma = 0.1 - 5.0$, $Nt = 0.1 - 0.5$, $Nb = 0.1 - 0.3$, $\delta t = \delta c = 0.1 - 0.5$, and $Kr = 0.1 - 1.0$ indicates that the values of the magnetic field, relaxation times, Hall currents, and diffusion of nanoparticles have a considerable effect on the flow, thermal, and concentration fields. The results have interesting applications in polymer extrusion, thermal control of nano-devices, magnetic drug delivery, and manufacturing smart materials.
SN  - 3069-1877
PB  - Institute of Central Computation and Knowledge
LA  - English
ER  -
BibTeX Format
Compatible with LaTeX, BibTeX, and other reference managers
BibTeX format data for LaTeX and reference managers
@article{Riaz2025Thermal,
  author = {Nimra Riaz and Muhammad Sohail},
  title = {Thermal and Chemical Dynamics in Magnetohydrodynamic Williamson Fluid Flow over a Stretching Cylinder under Heat/Mass Flux Effects Using Optimal Homotopy Analysis Method},
  journal = {International Journal of Thermo-Fluid Systems and Sustainable Energy},
  year = {2025},
  volume = {1},
  number = {2},
  pages = {46-63},
  doi = {10.62762/IJTSSE.2025.383195},
  url = {https://www.icck.org/article/abs/IJTSSE.2025.383195},
  abstract = {The knowledge on understanding non-Newtonian fluid dynamics influences and behaviors in magnetic and nanoscale effects of transport is also important to the advanced processes of engineering. The current paper examines MHD flow and heat transfer of a Williamson nanofluid across a stretching cylindrical surface, taking into consideration Hall current and chemical reaction and non-Fourier heat and mass flux that is described by the Cattaneo Christov theory. The transport of Nanoparticles is explained in terms of Buongiorno model of thermophoresis and Brownian movement. Similarity variables are used to transform the governing nonlinear equations and then analytically solved via Optimal Homotopy Analysis Method. The parametric study of parameters like \$M = 0.5 - 2.0\$, \$\gamma = 0.1 - 5.0\$, \$Nt = 0.1 - 0.5\$, \$Nb = 0.1 - 0.3\$, \$\delta t = \delta c = 0.1 - 0.5\$, and \$Kr = 0.1 - 1.0\$ indicates that the values of the magnetic field, relaxation times, Hall currents, and diffusion of nanoparticles have a considerable effect on the flow, thermal, and concentration fields. The results have interesting applications in polymer extrusion, thermal control of nano-devices, magnetic drug delivery, and manufacturing smart materials.},
  keywords = {williamson fluid, Magnetohydrodynamics (MHD), hall effect, buongiorno model, cattaneo-christov flux, chemical reaction, nanofluid, stretched cylinder, optimal homotopy analysis method},
  issn = {3069-1877},
  publisher = {Institute of Central Computation and Knowledge}
}
Article Metrics
Citations:

Google Scholar
0

Crossref

0

Scopus

0

Web of Science

0
Article Access Statistics:
Views: 139
PDF Downloads: 80
Publisher's Note
ICCK stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and Permissions
CC BY Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
International Journal of Thermo-Fluid Systems and Sustainable Energy

International Journal of Thermo-Fluid Systems and Sustainable Energy

ISSN: 3069-1877 (Online)

Email: [email protected]

Portico

Portico

All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/