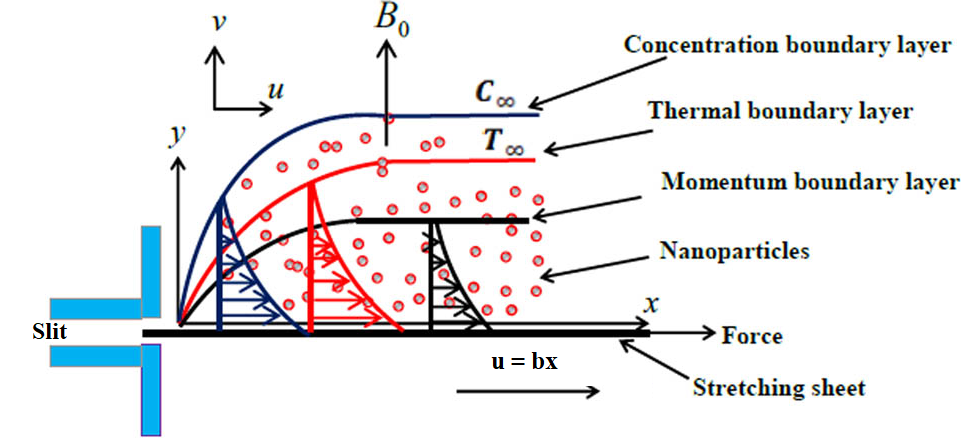
This study presents the application of the Artificial Neural Network Backpropagation Levenberg-Marquardt (ANN-BLMS) model for solving the nonlinear system of equations governing the flow of Casson-Williamson nanofluid under the influence of a magnetic field, Brownian motion, and thermophoresis effects. The model was trained using MATLAB's "bvp4c" solver to generate a reference dataset for various flow scenarios. Graphs having significant interest such as Nusselt Number are plotted and performance evaluation was carried out across multiple scenarios, which included variations in parameters such as Prandtl number, Weissenberg number, and Brownian motion coefficient. The results demonstrate that the ANN-BLMS model effectively minimizes the Mean Squared Error (MSE), achieving high accuracy across all cases. The model achieved an MSE as low as 5.36e-09, indicating strong performance in predicting the behaviour of the nanofluid. The model exhibited good generalization with minimal differences between training, validation, and testing errors, confirming its robustness. Additionally, the ANN-BLMS model showed efficient convergence, with fast computational times and the ability to handle complex flow dynamics involving magnetic field effects. These findings highlight the potential of using ANN for solving complex fluid dynamics problems in nanofluid systems, offering a reliable tool for practical applications in engineering and thermal management.