A Comparison of Evolutionary Computation Techniques for Parameter Estimation of Chaotic Systems

Jorge Gálvez; Gustavo R. Hernández; Omar Avalos; Angel Casas-Ordaz; Marco Perez-Cinseros; Diego Oliva

doi:10.62762/TSEL.2025.913117

CiteScore

Impact Factor

Volume 1, Issue 2, ICCK Transactions on Swarm and Evolutionary Learning

Volume 1, Issue 2, 2025

Submit Manuscript Edit a Special Issue

Article QR Code

Scan the QR code for reading

Popular articles

Case Studies on Integrating Artificial Intelligence in Finance to Transform Decision Making and Risk Management for Enhanced Financial Outcomes Reinforcement Learning for Prompt Optimization in Language Models: A Comprehensive Survey of Methods, Representations, and Evaluation Challenges AI and the Future of Education: Advancing Personalized Learning and Intelligent Tutoring Systems Plant Disease Detection Using Deep Learning Techniques Modeling Brain Functional Networks Using Graph Neural Networks: A Review and Clinical Application Bridging Modalities: A Survey of Cross-Modal Image-Text Retrieval Acrylamide in Food: Sources and Prevention Enhancing Fake News Detection with a Hybrid NLP-Machine Learning Framework Research on A Ship Trajectory Classification Method Based on Deep Learning Analyzing the Translation and Impact of Popular Science Literature in China: A Case Study Approach

ICCK Transactions on Swarm and Evolutionary Learning, Volume 1, Issue 2, 2025: 83-93

Free to Read | Research Article | 20 December 2025

A Comparison of Evolutionary Computation Techniques for Parameter Estimation of Chaotic Systems

Jorge Gálvez 1

Gustavo R. Hernández 1

Omar Avalos 1

Angel Casas-Ordaz 1 *

Marco Perez-Cinseros 1

Diego Oliva 1

1 Departamento de Ingeniería Electro-Fotónica, Centro Universitario de Ciencias Exactas e Ingenierías (CUCEI), Universidad de Guadalajara, Guadalajara, Jalisco 44430, México

* Corresponding Author: Angel Casas-Ordaz, [email protected]

DOI: 10.62762/TSEL.2025.913117

Received: 21 August 2025, Accepted: 28 November 2025, Published: 20 December 2025

PDF (3.19 MB)

Article Metrics Cite This Article

Abstract

In recent years, Parameter Estimation (PE) has become a topic of growing interest due to its broad applications in science and engineering. An important application is the identification of Chaotic Systems (CS), which enables synchronization and control of chaotic behavior. However, the parameter estimation of CS is a highly nonlinear and multidimensional optimization problem where traditional approaches are often unsuitable. To overcome these limitations, Evolutionary Computation Techniques (ECT) have been widely adopted to tackle complex nonlinear optimization tasks. Recently, classical and modern ECT methods have been proposed for estimating the parameters of chaotic systems. However, most reported studies rely exclusively on cost function values, overlooking the quality and consistency of the solutions obtained. This paper presents a comparative study of representative evolutionary techniques for estimating the parameters of chaotic systems. The study assesses the performance of the techniques and the homogeneity of the solutions through statistical analysis. Experimental results on the Lorenz and Chen systems are examined and validated using nonparametric tests.

Graphical Abstract

Keywords

evolutionary computation

chaotic systems

lorenz system

chen system

Data Availability Statement

Data will be made available on request.

Funding

This work was supported without any funding.

Conflicts of Interest

The authors declare no conflicts of interest.

Ethical Approval and Consent to Participate

Not applicable.

References

Zhou, X., Yang, C., & Gui, W. (2014). Nonlinear system identification and control using state transition algorithm. Applied mathematics and computation, 226, 169-179.
[CrossRef] [Google Scholar]
Ljung, L. (1999). System identification: theory for the user. Upper Saddle River, N.
[Google Scholar]
Pai, P. F., Nguyen, B. A., & Sundaresan, M. J. (2013). Nonlinearity identification by time-domain-only signal processing. International Journal of Non-Linear Mechanics, 54, 85-98.
[CrossRef] [Google Scholar]
Yang, S. K., Chen, C. L., & Yau, H. T. (2002). Control of chaos in Lorenz system. Chaos, Solitons & Fractals, 13(4), 767-780.
[CrossRef] [Google Scholar]
Yassen, M. T. (2003). Chaos control of Chen chaotic dynamical system. Chaos, Solitons and Fractals, 15(2), 271–283.
[CrossRef] [Google Scholar]
Kennedy, J., & Eberhart, R. (1995, November). Particle swarm optimization. In Proceedings of ICNN'95-international conference on neural networks (Vol. 4, pp. 1942-1948). IEEE.
[CrossRef] [Google Scholar]
Karaboga, D. (2005). An idea based on honey bee swarm for numerical optimization (Technical Report No. TR06). Department of Computer Engineering, Engineering Faculty, Erciyes University.
[Google Scholar]
Geem, Z. W., Kim, J. H., & Loganathan, G. V. (2001). A new heuristic optimization algorithm: harmony search. simulation, 76(2), 60-68.
[CrossRef] [Google Scholar]
Storn, R., & Price, K. (1997). Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. Journal of global optimization, 11(4), 341-359.
[CrossRef] [Google Scholar]
Yang, X. S., & Deb, S. (2009, December). Cuckoo search via Lévy flights. In 2009 World congress on nature & biologically inspired computing (NaBIC) (pp. 210-214). IEEE.
[CrossRef] [Google Scholar]
Rashedi, E., Nezamabadi-Pour, H., & Saryazdi, S. (2009). GSA: a gravitational search algorithm. Information sciences, 179(13), 2232-2248.
[CrossRef] [Google Scholar]
Cuevas, E., Gálvez, J., Hinojosa, S., Avalos, O., Zaldívar, D., & Pérez-Cisneros, M. (2014). A comparison of evolutionary computation techniques for IIR model identification. Journal of Applied Mathematics, 2014(1), 827206.
[CrossRef] [Google Scholar]
Wolpert, D. H., & Macready, W. G. (1997). No free lunch theorems for optimization. IEEE transactions on evolutionary computation, 1(1), 67-82.
[CrossRef] [Google Scholar]
Ahn, C. W. (2006). Advances in evolutionary algorithms: theory, design and practice. Berlin, Heidelberg: Springer Berlin Heidelberg.
[CrossRef] [Google Scholar]
Chiong, R., & Weise, T. (2012). Variants of evolutionary algorithms for real-world applications (Vol. 2). Z. Michalewicz (Ed.). Berlin: Springer.
[CrossRef] [Google Scholar]
Oltean, M. (2007). Evolving evolutionary algorithms with patterns. Soft Computing, 11(6), 503-518.
[CrossRef] [Google Scholar]
Lin, Y. L., Chang, W. D., & Hsieh, J. G. (2008). A particle swarm optimization approach to nonlinear rational filter modeling. Expert Systems with Applications, 34(2), 1194-1199.
[CrossRef] [Google Scholar]
Pavlyukevich, I. (2007). Lévy flights, non-local search and simulated annealing. Journal of Computational Physics, 226(2), 1830--1844.
[CrossRef] [Google Scholar]
Mantegna, R. N. (1994). Fast, accurate algorithm for numerical simulation of Levy stable stochastic processes. Physical Review E, 49(5), 4677.
[CrossRef] [Google Scholar]
De Jong, K. (1988). Learning with genetic algorithms: An overview. Machine Learning, 3, 121–138.
[CrossRef] [Google Scholar]
Hegazi, A. S., Ahmed, E., & Matouk, A. E. (2011). The effect of fractional order on synchronization of two fractional order chaotic and hyperchaotic systems. Journal of Fractional Calculus and Applications, 1(3), 1-15.
[Google Scholar]
Huang, L., Feng, R., & Wang, M. (2004). Synchronization of chaotic systems via nonlinear control. Physics Letters A, 320(4), 271–275.
[CrossRef] [Google Scholar]
He, Q., Wang, L., & Liu, B. (2007). Parameter estimation for chaotic systems by particle swarm optimization. Chaos, Solitons and Fractals, 34(2), 654–661.
[CrossRef] [Google Scholar]
Patwardhan, A. P., Patidar, R., & George, N. V. (2014). On a cuckoo search optimization approach towards feedback system identification. Digital Signal Processing, 32, 156-163.
[CrossRef] [Google Scholar]
García, S., Molina, D., Lozano, M., & Herrera, F. (2009). A study on the use of non-parametric tests for analyzing the evolutionary algorithms’ behaviour: a case study on the CEC’2005 special session on real parameter optimization. Journal of Heuristics, 15(6), 617-644.
[CrossRef] [Google Scholar]
Shilane, D., Martikainen, J., Dudoit, S., & Ovaska, S. J. (2008). A general framework for statistical performance comparison of evolutionary computation algorithms. Information Sciences, 178(14), 2870-2879.
[CrossRef] [Google Scholar]
Bonferroni, C. E. (1935). Il calcolo delle assicurazioni su gruppi di teste. Studi in Onore del Professor Salvatore Ortu Carboni, 13–60.
[Google Scholar]

Cite This Article

APA Style

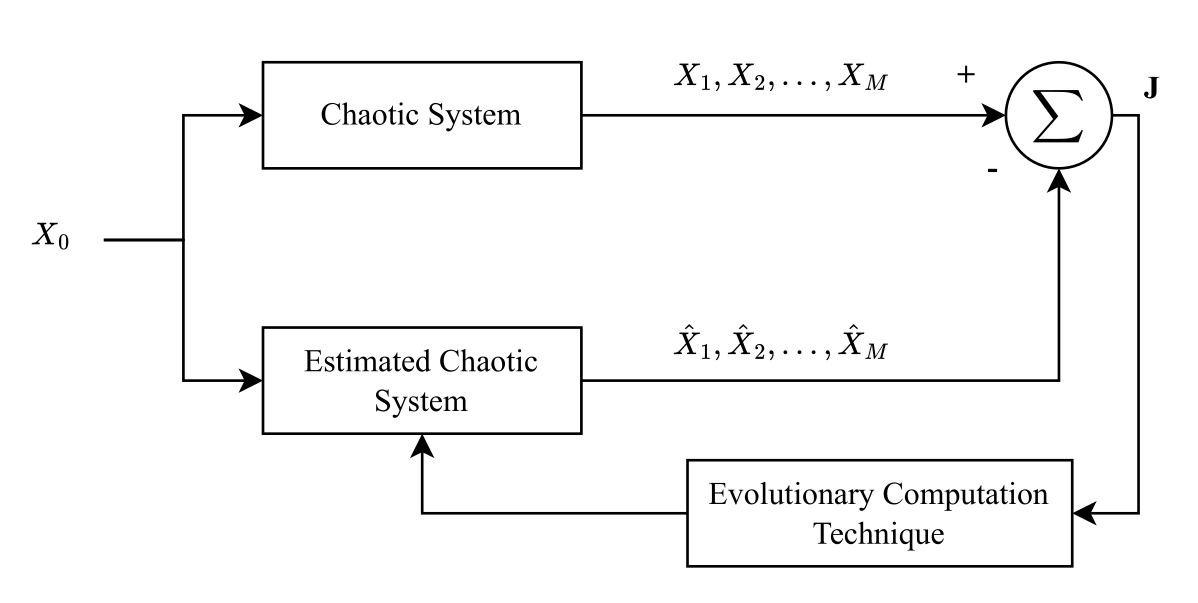
Gálvez, J., Hernández, G. R., Avalos, O., Casas-Ordaz, A., Perez-Cinseros, M., & Oliva, D. (2025). A Comparison of Evolutionary Computation Techniques for Parameter Estimation of Chaotic Systems. ICCK Transactions on Swarm and Evolutionary Learning, 1(2), 83–93. https://doi.org/10.62762/TSEL.2025.913117

Export Citation

RIS Format

Compatible with EndNote, Zotero, Mendeley, and other reference managers

RIS format data for reference managers

TY - JOUR
AU - Gálvez, Jorge
AU - Hernández, Gustavo R.
AU - Avalos, Omar
AU - Casas-Ordaz, Angel
AU - Perez-Cinseros, Marco
AU - Oliva, Diego
PY - 2025
DA - 2025/12/20
TI - A Comparison of Evolutionary Computation Techniques for Parameter Estimation of Chaotic Systems
JO - ICCK Transactions on Swarm and Evolutionary Learning
T2 - ICCK Transactions on Swarm and Evolutionary Learning
JF - ICCK Transactions on Swarm and Evolutionary Learning
VL - 1
IS - 2
SP - 83
EP - 93
DO - 10.62762/TSEL.2025.913117
UR - https://www.icck.org/article/abs/TSEL.2025.913117
KW - evolutionary computation
KW - chaotic systems
KW - lorenz system
KW - chen system
AB - In recent years, Parameter Estimation (PE) has become a topic of growing interest due to its broad applications in science and engineering. An important application is the identification of Chaotic Systems (CS), which enables synchronization and control of chaotic behavior. However, the parameter estimation of CS is a highly nonlinear and multidimensional optimization problem where traditional approaches are often unsuitable. To overcome these limitations, Evolutionary Computation Techniques (ECT) have been widely adopted to tackle complex nonlinear optimization tasks. Recently, classical and modern ECT methods have been proposed for estimating the parameters of chaotic systems. However, most reported studies rely exclusively on cost function values, overlooking the quality and consistency of the solutions obtained. This paper presents a comparative study of representative evolutionary techniques for estimating the parameters of chaotic systems. The study assesses the performance of the techniques and the homogeneity of the solutions through statistical analysis. Experimental results on the Lorenz and Chen systems are examined and validated using nonparametric tests.
SN - 3069-2962
PB - Institute of Central Computation and Knowledge
LA - English
ER -

BibTeX Format

Compatible with LaTeX, BibTeX, and other reference managers

BibTeX format data for LaTeX and reference managers

@article{Glvez2025A,
  author = {Jorge Gálvez and Gustavo R. Hernández and Omar Avalos and Angel Casas-Ordaz and Marco Perez-Cinseros and Diego Oliva},
  title = {A Comparison of Evolutionary Computation Techniques for Parameter Estimation of Chaotic Systems},
  journal = {ICCK Transactions on Swarm and Evolutionary Learning},
  year = {2025},
  volume = {1},
  number = {2},
  pages = {83-93},
  doi = {10.62762/TSEL.2025.913117},
  url = {https://www.icck.org/article/abs/TSEL.2025.913117},
  abstract = {In recent years, Parameter Estimation (PE) has become a topic of growing interest due to its broad applications in science and engineering. An important application is the identification of Chaotic Systems (CS), which enables synchronization and control of chaotic behavior. However, the parameter estimation of CS is a highly nonlinear and multidimensional optimization problem where traditional approaches are often unsuitable. To overcome these limitations, Evolutionary Computation Techniques (ECT) have been widely adopted to tackle complex nonlinear optimization tasks. Recently, classical and modern ECT methods have been proposed for estimating the parameters of chaotic systems. However, most reported studies rely exclusively on cost function values, overlooking the quality and consistency of the solutions obtained. This paper presents a comparative study of representative evolutionary techniques for estimating the parameters of chaotic systems. The study assesses the performance of the techniques and the homogeneity of the solutions through statistical analysis. Experimental results on the Lorenz and Chen systems are examined and validated using nonparametric tests.},
  keywords = {evolutionary computation, chaotic systems, lorenz system, chen system},
  issn = {3069-2962},
  publisher = {Institute of Central Computation and Knowledge}
}

Article Metrics

Citations:

Google Scholar

Crossref

Scopus

Web of Science

Article Access Statistics:

PDF Downloads: 8

Publisher's Note

ICCK stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and Permissions

Institute of Central Computation and Knowledge (ICCK) or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

ICCK Transactions on Swarm and Evolutionary Learning

ISSN: 3069-2962 (Online)

Email: [email protected]

Portico

All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/