ICCK Transactions on Systems Safety and Reliability
ISSN: 3069-1087 (Online)
Email: [email protected]
 Submit Manuscript
Edit a Special Issue
Submit Manuscript
Edit a Special Issue
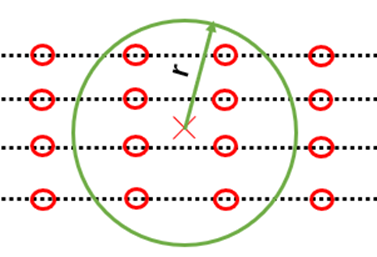
TY - JOUR AU - Hou, Chenglong AU - Zha, Yuhao AU - Yang, Jun AU - Wang, Ning PY - 2026 DA - 2026/02/03 TI - Distribution Field Construction and Prediction Method for Gas Leakage based on Kriging model and Gaussian Process JO - ICCK Transactions on Systems Safety and Reliability T2 - ICCK Transactions on Systems Safety and Reliability JF - ICCK Transactions on Systems Safety and Reliability VL - 2 IS - 1 SP - 11 EP - 25 DO - 10.62762/TSSR.2025.861997 UR - https://www.icck.org/article/abs/TSSR.2025.861997 KW - gas leakage KW - field prediction KW - kriging model KW - markov random field KW - neighborhood structure KW - gaussian process AB - Gas leakage poses a significant hazard in chemical industry operations, where failure to respond rapidly to gas diffusion can lead to poisoning, fire, or explosion. Timely and accurate prediction of gas dispersion is therefore essential for emergency decision-making and operational safety. While existing methods such as computational fluid dynamics, spatiotemporal statistics, and surrogate models emphasize prediction accuracy, they often suffer from excessive computational delays—especially critical in leak scenarios where casualties can occur within minutes. To address this gap, this paper introduces a Gaussian process-Markov random field-Kriging (GP-MRF-K) model for fast and reliable prediction of gas concentration fields. The approach integrates Markov random field (MRF) neighborhood structures into Kriging-based spatial interpolation, reducing computational complexity from O(n³) to O(n·m³), where n is the total grid points and m is the average neighbor count. Gas concentration time series are forecasted using Gaussian process regression (GPR), and the MRF-Kriging framework rapidly reconstructs the full concentration field. Validation with real ammonia concentration data from a warehouse-scale experimental setup confirms the feasibility and superiority of GP-MRF-K. With 150 training points and 10 prediction steps, the model achieves an MSE of 4660 and RMSE of 68.26, improving MSE by 67% over GPR-K (MSE=14003) and 87% over LSTM-K (MSE=36172), while attaining an R² of 0.9847. Computation time is reduced to 39.04 seconds, a 21.5% gain over GPR-K (49.72s) and a 98% reduction compared to LSTM-K (1990.85s), thereby meeting real-time emergency response requirements. SN - 3069-1087 PB - Institute of Central Computation and Knowledge LA - English ER -
@article{Hou2026Distributi,
author = {Chenglong Hou and Yuhao Zha and Jun Yang and Ning Wang},
title = {Distribution Field Construction and Prediction Method for Gas Leakage based on Kriging model and Gaussian Process},
journal = {ICCK Transactions on Systems Safety and Reliability},
year = {2026},
volume = {2},
number = {1},
pages = {11-25},
doi = {10.62762/TSSR.2025.861997},
url = {https://www.icck.org/article/abs/TSSR.2025.861997},
abstract = {Gas leakage poses a significant hazard in chemical industry operations, where failure to respond rapidly to gas diffusion can lead to poisoning, fire, or explosion. Timely and accurate prediction of gas dispersion is therefore essential for emergency decision-making and operational safety. While existing methods such as computational fluid dynamics, spatiotemporal statistics, and surrogate models emphasize prediction accuracy, they often suffer from excessive computational delays—especially critical in leak scenarios where casualties can occur within minutes. To address this gap, this paper introduces a Gaussian process-Markov random field-Kriging (GP-MRF-K) model for fast and reliable prediction of gas concentration fields. The approach integrates Markov random field (MRF) neighborhood structures into Kriging-based spatial interpolation, reducing computational complexity from O(n³) to O(n·m³), where n is the total grid points and m is the average neighbor count. Gas concentration time series are forecasted using Gaussian process regression (GPR), and the MRF-Kriging framework rapidly reconstructs the full concentration field. Validation with real ammonia concentration data from a warehouse-scale experimental setup confirms the feasibility and superiority of GP-MRF-K. With 150 training points and 10 prediction steps, the model achieves an MSE of 4660 and RMSE of 68.26, improving MSE by 67\% over GPR-K (MSE=14003) and 87\% over LSTM-K (MSE=36172), while attaining an R² of 0.9847. Computation time is reduced to 39.04 seconds, a 21.5\% gain over GPR-K (49.72s) and a 98\% reduction compared to LSTM-K (1990.85s), thereby meeting real-time emergency response requirements.},
keywords = {gas leakage, field prediction, kriging model, markov random field, neighborhood structure, gaussian process},
issn = {3069-1087},
publisher = {Institute of Central Computation and Knowledge}
}
ICCK Transactions on Systems Safety and Reliability
ISSN: 3069-1087 (Online)
Email: [email protected]

Portico
All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/