International Journal of Thermo-Fluid Systems and Sustainable Energy Home About Editors Current Issue
  1. Home
  2. Journals
  3. International Journal of Thermo-Fluid Systems and Sustainable Energy
  4. Volume 1, Issue 2
Thermal Cooling and System Irreversibilities of A Divergent/Convergent Channel with The Bioconvection Flow of Non-Newtonian Nanofluid
Research Article | Published: 22 December 2025
International Journal of Thermo-Fluid Systems and Sustainable Energy Volume 1, Issue 2, 2025: 83-95
Volume 1, Issue 2, International Journal of Thermo-Fluid Systems and Sustainable Energy
Volume 1, Issue 2, 2025
Submit Manuscript Edit a Special Issue
Article QR Code
Article QR Code
Scan the QR code for reading
Popular articles
Case Studies on Integrating Artificial Intelligence in Finance to Transform Decision Making and Risk Management for Enhanced Financial Outcomes Reservoir Science: A Multi-Coupling Communication Platform to Promote Energy Transformation, Climate Change and Environmental Protection Reinforcement Learning for Prompt Optimization in Language Models: A Comprehensive Survey of Methods, Representations, and Evaluation Challenges From CO$_2$ Sequestration to Hydrogen Storage: Further Utilization of Depleted Gas Reservoirs AI and the Future of Education: Advancing Personalized Learning and Intelligent Tutoring Systems Effects of Crosslinking Agents and Reservoir Conditions on the Propagation of Fractures in Coal Reservoirs During Hydraulic Fracturing The Influence of Geological Factors and Transmission Fluids on the Exploitation of Reservoir Geothermal Resources: Factor Discussion and Mechanism Analysis YOLOv8-Lite: A Lightweight Object Detection Model for Real-time Autonomous Driving Systems Plant Disease Detection Using Deep Learning Techniques Modeling Brain Functional Networks Using Graph Neural Networks: A Review and Clinical Application
International Journal of Thermo-Fluid Systems and Sustainable Energy, Volume 1, Issue 2, 2025: 83-95

Open Access | Research Article | 22 December 2025
Thermal Cooling and System Irreversibilities of A Divergent/Convergent Channel with The Bioconvection Flow of Non-Newtonian Nanofluid
by
Muhammad Eisa Muhammad Eisa 1
Sohail Rehman Sohail Rehman 2 *
Yasir Khan Yasir Khan 2
Maryam Maryam 2
Gulzar Ali Khan Gulzar Ali Khan 2
1 Department of Statistics, University of Peshawar, Peshawar 25000, Khyber Pakhtunkhwa, Pakistan
2 Department of Physical and Numerical Sciences, Qurtuba University of Science and Information Technology, Peshawar 25000, Khyber Pakhtunkhwa, Pakistan
* Corresponding Author: Sohail Rehman, [email protected]
DOI: 10.62762/IJTSSE.2025.318713
ARK: ark:/57805/ijtsse.2025.318713
Received: 01 December 2025, Accepted: 17 December 2025, Published: 22 December 2025  
   PDF  (3.06 MB)
Article Metrics Cite This Article
Abstract
The laminar bioconvection flow of a nanofluid in a convergent/divergent channel is computationally analyzed. The channel features impervious, adiabatic walls. A physics-based model couples the mass, momentum, and energy conservation equations. A thermal-hydraulic and entropy production analysis is performed using the first and second laws of thermodynamics to identify ideal parameters that maximize thermal performance while minimizing system irreversibility. Fluid flow, heat-mass transfer, motile microorganism density, and system entropy are investigated as functions of the channel angle. The governing equations are reduced via scaling and solved numerically using the Keller-Box method. Results indicate that higher Reynolds numbers and cross-viscosity reduce frictional drag, while motile density decreases with the Péclet number. Heat and mass transfer rates decline with increased Brownian motion, whereas thermophoresis shows opposing effects. Nanoparticle diffusion mitigates channel overheating, aiding thermal cooling. System irreversibilities dominate in narrower sections, and entropy generation near the wall increases with thermophoresis.
Graphical Abstract
Thermal Cooling and System Irreversibilities of A Divergent/Convergent Channel with The Bioconvection Flow of Non-Newtonian Nanofluid
Keywords
non-Newtonian fluid
converging/diverging flow
frictional drag
thermodynamic analysis
keller-Box approach
thermal cooling
Data Availability Statement
Data will be made available on request.
Funding
This work was supported without any funding.
Conflicts of Interest
The authors declare no conflicts of interest.
Ethical Approval and Consent to Participate
Not applicable.
References
  1. Abegunrin, O. A., Animasaun, I. L., & Sandeep, N. (2018). Insight into the boundary layer flow of non-Newtonian Eyring-Powell fluid due to catalytic surface reaction on an upper horizontal surface of a paraboloid of revolution. Alexandria Engineering Journal, 57(3), 2051–2060.
    [CrossRef]   [Google Scholar]
  2. Adesanya, S. O., & Makinde, O. D. (2015). Irreversibility analysis in a couple stress film flow along an inclined heated plate with adiabatic free surface. Physica A: Statistical Mechanics and its Applications, 432, 222–229.
    [CrossRef]   [Google Scholar]
  3. Puneeth, V., Narayan, S. S., Manjunatha, S., & Makinde, O. D. (2022). Numerical simulation of Jeffrey–Hamel flow of nanofluid in the presence of gyrotactic microorganisms. International Journal of Ambient Energy, 43(1), 6095-6107.
    [CrossRef]   [Google Scholar]
  4. Avramenko, A. A., Kovetska, Y. Y., & Shevchuk, I. V. (2023). Lorenz approach for analysis of bioconvection instability of gyrotactic motile microorganisms. Chaos, Solitons & Fractals, 166, 112957.
    [CrossRef]   [Google Scholar]
  5. Banerjee, A., Mahato, S. K., Bhattacharyya, K., & Chamkha, A. J. (2021). Divergent channel flow of Casson fluid and heat transfer with suction/blowing and viscous dissipation: Existence of boundary layer. Partial Differential Equations in Applied Mathematics, 4, 100172.
    [CrossRef]   [Google Scholar]
  6. Barzegar Gerdroodbary, M., Rahimi Takami, M., & Ganji, D. D. (2015). Investigation of thermal radiation on traditional Jeffery–Hamel flow to stretchable convergent/divergent channels. Case Studies in Thermal Engineering, 6, 28–39.
    [CrossRef]   [Google Scholar]
  7. Bejan, A. (1979). A Study of Entropy Generation in Fundamental Convective Heat Transfer. Journal of Heat Transfer, 101(4), 718–725.
    [CrossRef]   [Google Scholar]
  8. Boudjemline, A., Ahmad, I., Rehman, S., Hashim, & Khedher, N. B. (2023). Jeffery-Hamel flow extension and thermal analysis of Oldroyd-B NF in expanding channel. Journal of Non-Equilibrium Thermodynamics, 48(1), 75–90.
    [CrossRef]   [Google Scholar]
  9. Boujelbene, M., Rehman, S., Alqahtani, S., & Alshehery, S. (2023). Second law assessment of injected nanoparticles to blood flow with thermal radiation and magnetic field in conduit artery. Journal of the Taiwan Institute of Chemical Engineers, 150, 105074.
    [CrossRef]   [Google Scholar]
  10. Arain, M. B., Bhatti, M. M., Zeeshan, A., & Alzahrani, F. S. (2021). Bioconvection Reiner-Rivlin nanofluid flow between rotating circular plates with induced magnetic effects, activation energy and squeezing phenomena. Mathematics, 9(17), 2139.
    [CrossRef]   [Google Scholar]
  11. Bouzidi, M., Maleki, H., Ambreen, T., Gholami, M., Tlili, I., & Khan, M. I. (2025). Exploring Darcy-Brinkman model and magnetic dipole impact on heat and mass transfer of Stefan blowing slip flow of ferromagnetic Prandtl NF. Case Studies in Thermal Engineering, 75, 106999.
    [CrossRef]   [Google Scholar]
  12. Cebeci, T., & Bradshaw, P. (2012). Physical and Computational Aspects of Convective Heat Transfer. Springer Science & Business Media.
    [Google Scholar]
  13. Chu, Y. M., Ahmad, F., Khan, M. I., Nazeer, M., Hussain, F., Khan, N. B., ... & Mei, L. (2021). Numerical and scale analysis of non-Newtonian fluid (Eyring-Powell) through pseudo-spectral collocation method (PSCM) towards a magnetized stretchable Riga surface. Alexandria Engineering Journal, 60(2), 2127-2137.
    [CrossRef]   [Google Scholar]
  14. Sparrow, E. M., Abraham, J. P., & Minkowycz, W. J. (2009). Flow separation in a diverging conical duct: Effect of Reynolds number and divergence angle. International Journal of Heat and Mass Transfer, 52(13-14), 3079-3083.
    [CrossRef]   [Google Scholar]
  15. Gamaoun, F., Ullah, Z., Ahammad, N. A., Fadhl, B. M., Makhdoum, B. M., & Khan, A. A. (2023). Effects of thermal radiation and variable density of NF heat transfer along a stretching sheet by using Keller Box approach under magnetic field. Thermal Science and Engineering Progress, 41, 101815.
    [CrossRef]   [Google Scholar]
  16. Garimella, S. M., Anand, M., & Rajagopal, K. R. (2022). Jeffery–Hamel flow of a shear-thinning fluid that mimics the response of viscoplastic materials. International Journal of Non-Linear Mechanics, 144, 104084.
    [CrossRef]   [Google Scholar]
  17. Haines, P. E., Hewitt, R. E., & Hazel, A. L. (2011). The Jeffery–Hamel similarity solution and its relation to flow in a diverging channel. Journal of Fluid Mechanics, 687, 404–430.
    [CrossRef]   [Google Scholar]
  18. Hamel, G. (1917). Spiralförmige Bewegungen zäher Flüssigkeiten. Jahresbericht der Deutschen Mathematiker-Vereinigung, 25, 34–60.
    [Google Scholar]
  19. Harley, C., Momoniat, E., & Rajagopal, K. R. (2018). Reversal of flow of a non-Newtonian fluid in an expanding channel. International Journal of Non-Linear Mechanics, 101, 44–55.
    [CrossRef]   [Google Scholar]
  20. Upreti, H., Pandey, A. K., Kumar, M., & Makinde, O. D. (2020). Ohmic heating and non-uniform heat source/sink roles on 3D Darcy–Forchheimer flow of CNTs nanofluids over a stretching surface. Arabian Journal for Science and Engineering, 45(9), 7705-7717.
    [CrossRef]   [Google Scholar]
  21. Jalili, B., Ganji, A. D., Jalili, P., Salman Nourazar, S., & Ganji, D. D. (2022). Thermal analysis of Williamson fluid flow with Lorentz force on the stretching plate. Case Studies in Thermal Engineering, 39, 102374.
    [CrossRef]   [Google Scholar]
  22. Jeffery, G. B. (1915). L. The two-dimensional steady motion of a viscous fluid. The London, Edinburgh, and Dublin philosophical magazine and journal of science, 29(172), 455-465.
    [CrossRef]   [Google Scholar]
  23. Jotkar, M. R., & Govindarajan, R. (2017). Non-modal stability of Jeffery-Hamel flow. Physics of Fluids, 29(6), 064107.
    [CrossRef]   [Google Scholar]
  24. Khan, S. A., Hayat, T., & Alsaedi, A. (2023). Bioconvection entropy optimized flow of Reiner-Rivlin nanoliquid with motile microorganisms. Alexandria Engineering Journal, 79, 81–92.
    [CrossRef]   [Google Scholar]
  25. Khan, U., Sikandar, W., Ahmed, N., & Mohyud-Din, S. T. (2016). Effects of Velocity Slip on MHD Flow of a Non-Newtonian Fluid in Converging and Diverging Channels. International Journal of Applied and Computational Mathematics, 2(4), 469–483.
    [CrossRef]   [Google Scholar]
  26. Torabi, M., Zhang, K., Karimi, N., & Peterson, G. P. (2016). Entropy generation in thermal systems with solid structures–a concise review. International Journal of Heat and Mass Transfer, 97, 917-931.
    [CrossRef]   [Google Scholar]
  27. Kumar, D., Ramesh, K., & Chandok, S. (2020). Mathematical modeling and simulation for the flow of magneto-Powell-Eyring fluid in an annulus with concentric rotating cylinders. Chinese Journal of Physics, 65, 187–197.
    [CrossRef]   [Google Scholar]
  28. Mahian, O., Kianifar, A., Sahin, A. Z., & Wongwises, S. (2014). Entropy generation during Al2O3/water NF flow in a solar collector: Effects of tube roughness, nanoparticle size, and different thermophysical models. International Journal of Heat and Mass Transfer, 78, 64–75.
    [CrossRef]   [Google Scholar]
  29. Mahian, O., Mahmud, S., & Heris, S. Z. (2012). Effect of Uncertainties in Physical Properties on Entropy Generation Between Two Rotating Cylinders With NF. Journal of Heat Transfer, 134(10), 101704.
    [CrossRef]   [Google Scholar]
  30. Mandal, S., Shit, G. C., Shaw, S., & Makinde, O. D. (2022). Entropy analysis of thermo-solutal stratification of NF flow containing gyrotactic microorganisms over an inclined radiative stretching cylinder. Thermal Science and Engineering Progress, 34, 101379.
    [CrossRef]   [Google Scholar]
  31. Mustafa, M., Ahmad Khan, J., Hayat, T., & Alsaedi, A. (2015). Analytical and numerical solutions for axisymmetric flow of NF due to non-linearly stretching sheet. International Journal of Non-Linear Mechanics, 71, 22–29.
    [CrossRef]   [Google Scholar]
  32. Nayak, M. K., Shaw, S., Ijaz Khan, M., Makinde, O. D., Chu, Y.-M., & Khan, S. U. (2021). Interfacial layer and shape effects of modified Hamilton’s Crosser model in entropy optimized Darcy-Forchheimer flow. Alexandria Engineering Journal, 60(4), 4067–4083.
    [CrossRef]   [Google Scholar]
  33. Nazeer, M., Khan, M. I., Rafiq, M. U., & Khan, N. B. (2020). Numerical and scale analysis of Eyring-Powell NF towards a magnetized stretched Riga surface with entropy generation and internal resistance. International Communications in Heat and Mass Transfer, 119, 104968.
    [CrossRef]   [Google Scholar]
  34. Nazeer, M., Hussain, F., Khan, M. I., Kadry, S., Chu, Y.-M., & Khan, S. U. (2019). Effects of Constant and Space-Dependent Viscosity on Eyring–Powell Fluid in a Pipe: Comparison of the Perturbation and Explicit Finite Difference Methods. Zeitschrift für Naturforschung A, 74(11), 961–969.
    [CrossRef]   [Google Scholar]
  35. Ojiambo, V., Kinyanjui, M., & Kimathi, M. (2018). A study of two-phase Jeffery Hamel flow in a geothermal pipe.
    [Google Scholar]
  36. Powell, R. E., & Eyring, H. (1944). Mechanisms for the Relaxation Theory of Viscosity. Nature, 154(3909), 427–428.
    [CrossRef]   [Google Scholar]
  37. Ullah, K., Fiza, M., Ullah, H., Jan, A. U., Akgül, A., Hendy, A., ... & Khan, I. (2025). Deep learning investigation of ternary hybrid nanofluid flow with nonlinear heat source-sink and Cattaneo-Christov heat flux model with Joule effect. Proceedings of the Institution of Mechanical Engineers, Part N: Journal of Nanomaterials, Nanoengineering and Nanosystems, 23977914251343344.
    [CrossRef]   [Google Scholar]
  38. Rehman, S., & NASR, S. (2025). Optimization of MHD Jeffrey-Hamel flow in convergent–divergent channels with slip and viscous-dissipation: vorticity–stream-function analysis of flow reversal and heat transfer. Journal of Taibah University for Science, 19(1), 2548630.
    [CrossRef]   [Google Scholar]
  39. Rehman, S., Almubaddel, F. S., Mahrous, Y. M., Alsadoun, F. A., Abouzied, A. S., & Hashim. (2023). A generalization of Jeffrey-Hamel problem to Reiner-Rivlin model for energy and thermodynamic analysis using Keller-Box computational framework. Case Studies in Thermal Engineering, 50, 103462.
    [CrossRef]   [Google Scholar]
  40. Rehman, S., Alqahtani, S., Hashim, & Alshehery, S. (2023). On the thermal performance during flow dynamics of viscoelastic fluid in a channel: Jaffrey–Hamel extension. Neural Computing and Applications, 35(29), 21949–21965.
    [CrossRef]   [Google Scholar]
  41. Rehman, S., Hashim, Alqahtani, S., Hadj Hassine, S. B., & Eldin, S. M. (2023). Thermohydraulic and irreversibility assessment of Power-law fluid flow within wedge shape channel. Arabian Journal of Chemistry, 16(3), 104475.
    [CrossRef]   [Google Scholar]
  42. Rehman, S., Al-Yarimi, F. A., Alqahtani, S., & Awad, M. (2023). Dissipative flow features of Carreau nanofluid with thermal radiation inside plane wall channel: Jeffery-Hamel analysis. Propulsion and Power Research, 12(2), 253-272.
    [CrossRef]   [Google Scholar]
  43. Sadeghy, K., Khabazi, N., & Taghavi, S.-M. (2007). Magnetohydrodynamic (MHD) flows of viscoelastic fluids in converging/diverging channels. International Journal of Engineering Science, 45(11), 923–938.
    [CrossRef]   [Google Scholar]
  44. Sahoo, B., & Shevchuk, I. V. (2019). Heat transfer due to revolving flow of Reiner-Rivlin fluid over a stretchable surface. Thermal Science and Engineering Progress, 10, 327–336.
    [CrossRef]   [Google Scholar]
  45. Salahuddin, T. (2020). Carreau fluid model towards a stretching cylinder: Using Keller box and shooting method. Ain Shams Engineering Journal, 11(2), 495–500.
    [CrossRef]   [Google Scholar]
  46. Salawu, S. O., Kareem, R. A., & Shonola, S. A. (2019). Radiative thermal criticality and entropy generation of hydromagnetic reactive Powell–Eyring fluid in saturated porous media with variable conductivity. Energy Reports, 5, 480–488.
    [CrossRef]   [Google Scholar]
  47. Sari, M. R., Kezzar, M., & Adjabi, R. (2016). Heat transfer of copper/water NF flow through converging-diverging channel. Journal of Central South University, 23(2), 484–496.
    [CrossRef]   [Google Scholar]
  48. Shah, S. O., Rehman, S., Osman, M., Afridi, S., Ben Hadj Hassine, S., & Ullah, U. (2024). Optimum thermal design for heat and mass transfer of non-Newtonian liquid within converging conduit with thermal jump and zero-mass flux. Case Studies in Thermal Engineering, 53, 103817.
    [CrossRef]   [Google Scholar]
  49. Shukla, N., Rana, P., & Pop, I. (2020). Second law thermodynamic analysis of thermo-magnetic Jeffery–Hamel dissipative radiative hybrid nanofluid slip flow: existence of multiple solutions. The European Physical Journal Plus, 135(10), 1-24.
    [CrossRef]   [Google Scholar]
  50. Shaw, S., Patra, A., Misra, A., & Nayak, M. K. (2022). Assisting/opposing/forced convection flow on entropy-optimized MHD NF with variable viscosity: Interfacial layer and shape effects. Heat Transfer, 51(1), 578–603.
    [CrossRef]   [Google Scholar]
  51. Shaw, S., Shit, G. C., & Tripathi, D. (2022). Impact of drug carrier shape, size, porosity and blood rheology on magnetic nanoparticle-based drug delivery in a microvessel. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 639, 128370.
    [CrossRef]   [Google Scholar]
  52. Sheikholeslami, M., Ganji, D. D., Ashorynejad, H. R., & Rokni, H. B. (2012). Analytical investigation of Jeffery-Hamel flow with high magnetic field and nanoparticle by Adomian decomposition method. Applied Mathematics and Mechanics (English Edition), 33(1), 25–36.
    [CrossRef]   [Google Scholar]
  53. Tadesse, F. B., Makinde, O. D., & Enyadene, L. G. (2021). Hydromagnetic stagnation point flow of a magnetite ferrofluid past a convectively heated permeable stretching/shrinking sheet in a Darcy–Forchheimer porous medium. Sādhanā, 46(3), 115.
    [CrossRef]   [Google Scholar]
  54. Verma, L., Meher, R., Hammouch, Z., & Baskonus, H. M. (2022). Effect of heat transfer on hybrid nanofluid flow in converging/diverging channel using fuzzy volume fraction. Scientific Reports, 12(1), 20845.
    [CrossRef]   [Google Scholar]
  55. Usman Rashid, M., & Mustafa, M. (2021). A study of heat transfer and entropy generation in von Kármán flow of Reiner-Rivlin fluid due to a stretchable disk. Ain Shams Engineering Journal, 12(1), 875–883.
    [CrossRef]   [Google Scholar]
Cite This Article
APA Style
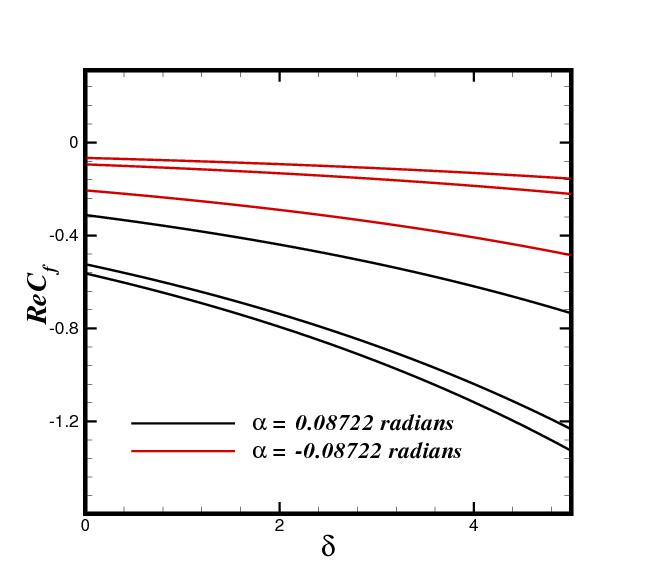
Eisa, M., Rehman, S., Khan, Y., Maryam, & Khan, G. A. (2025). Thermal Cooling and System Irreversibilities of A Divergent/Convergent Channel with The Bioconvection Flow of Non-Newtonian Nanofluid. International Journal of Thermo-Fluid Systems and Sustainable Energy, 1(2), 83–95. https://doi.org/10.62762/IJTSSE.2025.318713
Export Citation
RIS Format
Compatible with EndNote, Zotero, Mendeley, and other reference managers
RIS format data for reference managers
TY  - JOUR
AU  - Eisa, Muhammad
AU  - Rehman, Sohail
AU  - Khan, Yasir
AU  - Maryam
AU  - Khan, Gulzar Ali
PY  - 2025
DA  - 2025/12/22
TI  - Thermal Cooling and System Irreversibilities of A Divergent/Convergent Channel with The Bioconvection Flow of Non-Newtonian Nanofluid
JO  - International Journal of Thermo-Fluid Systems and Sustainable Energy
T2  - International Journal of Thermo-Fluid Systems and Sustainable Energy
JF  - International Journal of Thermo-Fluid Systems and Sustainable Energy
VL  - 1
IS  - 2
SP  - 83
EP  - 95
DO  - 10.62762/IJTSSE.2025.318713
UR  - https://www.icck.org/article/abs/IJTSSE.2025.318713
KW  - non-Newtonian fluid
KW  - converging/diverging flow
KW  - frictional drag
KW  - thermodynamic analysis
KW  - keller-Box approach
KW  - thermal cooling
AB  - The laminar bioconvection flow of a nanofluid in a convergent/divergent channel is computationally analyzed. The channel features impervious, adiabatic walls. A physics-based model couples the mass, momentum, and energy conservation equations. A thermal-hydraulic and entropy production analysis is performed using the first and second laws of thermodynamics to identify ideal parameters that maximize thermal performance while minimizing system irreversibility. Fluid flow, heat-mass transfer, motile microorganism density, and system entropy are investigated as functions of the channel angle. The governing equations are reduced via scaling and solved numerically using the Keller-Box method. Results indicate that higher Reynolds numbers and cross-viscosity reduce frictional drag, while motile density decreases with the Péclet number. Heat and mass transfer rates decline with increased Brownian motion, whereas thermophoresis shows opposing effects. Nanoparticle diffusion mitigates channel overheating, aiding thermal cooling. System irreversibilities dominate in narrower sections, and entropy generation near the wall increases with thermophoresis.
SN  - 3069-1877
PB  - Institute of Central Computation and Knowledge
LA  - English
ER  -
BibTeX Format
Compatible with LaTeX, BibTeX, and other reference managers
BibTeX format data for LaTeX and reference managers
@article{Eisa2025Thermal,
  author = {Muhammad Eisa and Sohail Rehman and Yasir Khan and Maryam and Gulzar Ali Khan},
  title = {Thermal Cooling and System Irreversibilities of A Divergent/Convergent Channel with The Bioconvection Flow of Non-Newtonian Nanofluid},
  journal = {International Journal of Thermo-Fluid Systems and Sustainable Energy},
  year = {2025},
  volume = {1},
  number = {2},
  pages = {83-95},
  doi = {10.62762/IJTSSE.2025.318713},
  url = {https://www.icck.org/article/abs/IJTSSE.2025.318713},
  abstract = {The laminar bioconvection flow of a nanofluid in a convergent/divergent channel is computationally analyzed. The channel features impervious, adiabatic walls. A physics-based model couples the mass, momentum, and energy conservation equations. A thermal-hydraulic and entropy production analysis is performed using the first and second laws of thermodynamics to identify ideal parameters that maximize thermal performance while minimizing system irreversibility. Fluid flow, heat-mass transfer, motile microorganism density, and system entropy are investigated as functions of the channel angle. The governing equations are reduced via scaling and solved numerically using the Keller-Box method. Results indicate that higher Reynolds numbers and cross-viscosity reduce frictional drag, while motile density decreases with the Péclet number. Heat and mass transfer rates decline with increased Brownian motion, whereas thermophoresis shows opposing effects. Nanoparticle diffusion mitigates channel overheating, aiding thermal cooling. System irreversibilities dominate in narrower sections, and entropy generation near the wall increases with thermophoresis.},
  keywords = {non-Newtonian fluid, converging/diverging flow, frictional drag, thermodynamic analysis, keller-Box approach, thermal cooling},
  issn = {3069-1877},
  publisher = {Institute of Central Computation and Knowledge}
}
Article Metrics
Citations:

Google Scholar
0

Crossref

0

Scopus

0

Web of Science

0
Article Access Statistics:
Views: 144
PDF Downloads: 72
Publisher's Note
ICCK stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and Permissions
CC BY Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
International Journal of Thermo-Fluid Systems and Sustainable Energy

International Journal of Thermo-Fluid Systems and Sustainable Energy

ISSN: 3069-1877 (Online)

Email: [email protected]

Portico

Portico

All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/