ICCK Journal of Applied Mathematics Home About Editors Current Issue
  1. Home
  2. Journals
  3. ICCK Journal of Applied Mathematics
  4. Volume 2, Issue 1
Equilibria and Stability Analysis of a Compartmental Model for Crime Dynamics with Recidivism and Corruption
Research Article | Published: 15 January 2026
ICCK Journal of Applied Mathematics Volume 2, Issue 1, 2026: 1-43
Volume 2, Issue 1, ICCK Journal of Applied Mathematics
Volume 2, Issue 1, 2026
Submit Manuscript Edit a Special Issue
Article QR Code
Article QR Code
Scan the QR code for reading
Popular articles
Case Studies on Integrating Artificial Intelligence in Finance to Transform Decision Making and Risk Management for Enhanced Financial Outcomes Reservoir Science: A Multi-Coupling Communication Platform to Promote Energy Transformation, Climate Change and Environmental Protection Reinforcement Learning for Prompt Optimization in Language Models: A Comprehensive Survey of Methods, Representations, and Evaluation Challenges From CO$_2$ Sequestration to Hydrogen Storage: Further Utilization of Depleted Gas Reservoirs AI and the Future of Education: Advancing Personalized Learning and Intelligent Tutoring Systems Effects of Crosslinking Agents and Reservoir Conditions on the Propagation of Fractures in Coal Reservoirs During Hydraulic Fracturing The Influence of Geological Factors and Transmission Fluids on the Exploitation of Reservoir Geothermal Resources: Factor Discussion and Mechanism Analysis YOLOv8-Lite: A Lightweight Object Detection Model for Real-time Autonomous Driving Systems Plant Disease Detection Using Deep Learning Techniques Modeling Brain Functional Networks Using Graph Neural Networks: A Review and Clinical Application
ICCK Journal of Applied Mathematics, Volume 2, Issue 1, 2026: 1-43

Open Access | Research Article | 15 January 2026
Equilibria and Stability Analysis of a Compartmental Model for Crime Dynamics with Recidivism and Corruption
by
Sarita Pippal Sarita Pippal 1 *
Ajay Ranga Ajay Ranga 2
1 Department of Mathematics, Panjab University, Chandigarh 160014, India
2 J.C. Bose University of Science & Technology, YMCA, Faridabad, Haryana 121006, India
* Corresponding Author: Sarita Pippal, [email protected]
DOI: 10.62762/JAM.2025.240326
ARK: ark:/57805/jam.2025.240326
Received: 25 October 2025, Accepted: 09 December 2025, Published: 15 January 2026  
   PDF  (3.75 MB)
Article Metrics Cite This Article
Abstract
A nonlinear compartmental model is developed to analyze crime dynamics in a structured society. The population is stratified into eight compartments: \(S(t)\) (susceptible), \(E(t)\) (exposed), \(C(t)\) (active criminals), \(C_v(t)\) (convicted criminals), \(P_h(t)\) (passive-honest), \(P_c(t)\) (committed-honest), \(J_h(t)\) (honest judges), and \(J_c(t)\) (corrupt judges). The model incorporates nonlinear mechanisms such as institutional corruption (\(\kappa_1\)), judicial correction (\(\kappa_2\)), recidivism feedback (\(\rho_1,\rho_2\)), exposure intensity (\(\eta_1\)), and rehabilitation (\(r_2\)), providing a realistic portrayal of crime--justice interactions. Solutions remain positive and bounded within a feasible domain \(\mathcal{D}\). Linear stability analysis of the crime--free equilibrium \(Z_0\) is performed via the Jacobian \(J(Z_0)\). Numerical simulations explore the long--term dynamics under variations of key parameters (\(\beta_1,\eta_1,\rho_1,\rho_2,r_2,\kappa_1,\kappa_2\)). Results show that strong judicial recruitment (\(a_1\)) and honest reinforcement (\(\beta_4\)) suppress criminal activity, whereas increased corruption (\(\kappa_1\)) and recidivism (\(\rho_1,\rho_2\)) promote its growth. Bifurcation curves, contour maps, and stability basins highlight critical thresholds and equilibrium structures. The analysis demonstrates that proactive policy measures---reducing corruption, discouraging recidivism, and enhancing judicial integrity---can significantly lower crime levels and foster honest societal behavior, offering valuable guidance for designing effective crime--prevention strategies across diverse socio--political contexts.
Graphical Abstract
Equilibria and Stability Analysis of a Compartmental Model for Crime Dynamics with Recidivism and Corruption
Keywords
dynamical systems
nonlinear system
differential equations
stability
bifurcation
Data Availability Statement
Data will be made available on request.
Funding
This work was supported without any funding.
Conflicts of Interest
The authors declare no conflicts of interest.
AI Use Statement
The authors declare that no generative AI was used in the preparation of this manuscript.
Ethical Approval and Consent to Participate
Not applicable. This is a theoretical mathematical modeling study using only publicly available aggregated data; no human participants were involved.
References
  1. United Nations. (2003). Manual for the Development of a System of Criminal Justice Statistics (Series F, No. 89). United Nations Statistics Division. Retrieved from https://unstats.un.org/unsd/methods/crime/
    [Google Scholar]
  2. Law, J. (Ed.). (2015). A dictionary of law. OUP Oxford.
    [Google Scholar]
  3. Schabbach, L. M. (2013). O crime organizado em perspectiva mundial. Sociologias, 15, 278–293.
    [CrossRef]   [Google Scholar]
  4. Balhara, Y. P. S., Sarkar, S., & Rajguru, A. J. (2024). Drug-related offences in India: Observations and insights from the secondary analysis of the data from the National Crimes Record Bureau. Indian Journal of Psychological Medicine, 46(6), 527-534.
    [CrossRef]   [Google Scholar]
  5. McMillon, D., Simon, C. P., & Morenoff, J. (2014). Modeling the underlying dynamics of the spread of crime. PloS one, 9(4), e88923.
    [CrossRef]   [Google Scholar]
  6. National Association for the Advancement of Colored People. (2011). Misplaced priorities: Over incarcerate, under educate Excessive spending on incarceration undermines educational opportunity and public safety in communities. National Institute of Justice. Retrieved from https://www.ncjrs.gov/App/Publications/abstract.aspx?ID=256929
    [Google Scholar]
  7. Wilson, J. Q., & Herrnstein, R. J. (1985). Crime and human nature. Simon and Schuster.
    [Google Scholar]
  8. Bandura, A., & Walters, R. H. (1977). Social learning theory (Vol. 1, pp. 141-154). Englewood Cliffs, NJ: Prentice hall.
    [Google Scholar]
  9. Becker, G. S. (1968). Crime and punishment: An economic approach. Journal of political economy, 76(2), 169-217.
    [CrossRef]   [Google Scholar]
  10. Burdett, K., Lagos, R., & Wright, R. (2004). An on‐the‐job search model of crime, inequality, and unemployment. International Economic Review, 45(3), 681-706.
    [CrossRef]   [Google Scholar]
  11. McMillon, D., Morenoff, J., Simon, C., & Lane, E. (2025). A dynamical systems analysis of criminal behavior using national longitudinal survey of youth data. Plos one, 20(8), e0324014.
    [CrossRef]   [Google Scholar]
  12. Short, M. B., Bertozzi, A. L., & Brantingham, P. J. (2010). Nonlinear patterns in urban crime: Hotspots, bifurcations, and suppression. SIAM Journal on Applied Dynamical Systems, 9(2), 462-483.
    [CrossRef]   [Google Scholar]
  13. Rodriguez, N., & Bertozzi, A. (2010). Local existence and uniqueness of solutions to a PDE model for criminal behavior. Mathematical Models and Methods in Applied Sciences, 20(supp01), 1425-1457.
    [CrossRef]   [Google Scholar]
  14. Manasevich, R., Phan, Q. H., & Souplet, P. (2013). Global existence of solutions for a chemotaxis-type system arising in crime modelling. European Journal of Applied Mathematics, 24(2), 273-296.
    [CrossRef]   [Google Scholar]
  15. Cantrell, R. S., Cosner, C., & Manásevich, R. (2012). Global bifurcation of solutions for crime modeling equations. SIAM Journal on Mathematical Analysis, 44(3), 1340-1358.
    [CrossRef]   [Google Scholar]
  16. Mohler, G. O., & Short, M. B. (2012). Geographic profiling from kinetic models of criminal behavior. SIAM Journal on Applied Mathematics, 72(1), 163-180.
    [CrossRef]   [Google Scholar]
  17. Misra, A. (2014). Modeling the effect of police deterrence on the prevalence of crime in the society. Applied Mathematics and Computation, 237, 531–545.
    [CrossRef]   [Google Scholar]
  18. Diekmann, O., Heesterbeek, J. A. P., & Roberts, M. G. (2010). The construction of next-generation matrices for compartmental epidemic models. Journal of the royal society interface, 7(47), 873-885.
    [CrossRef]   [Google Scholar]
  19. Bansal, S., Grenfell, B. T., & Meyers, L. A. (2007). When individual behaviour matters: homogeneous and network models in epidemiology. Journal of the Royal Society Interface, 4(16), 879-891.
    [CrossRef]   [Google Scholar]
  20. Van den Driessche, P., & Watmough, J. (2002). Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences, 180(1–2), 29–48.
    [CrossRef]   [Google Scholar]
  21. Glaeser, E. L., Sacerdote, B., & Scheinkman, J. A. (1996). Crime and social interactions. The Quarterly Journal of Economics, 111(2), 507–548.
    [CrossRef]   [Google Scholar]
  22. Pippal, S., Kapoor, S., & Ranga, A. (2025). Bifurcation and stability analysis with numerical simulations of a social model for marriage and divorce under fear effect. Nonlinear Science and Control Engineering, 1(1), 025290005. https://www.doi.org/10.36922/NSCE025290005
    [Google Scholar]
  23. National Crime Records Bureau, Ministry of Home Affairs. (2023). Crime in India 2022: Statistics (Volume-1). Government of India. Retrieved from https://images.assettype.com/barandbench/2023-12/dc0ba053-a1f0-4e6a-a5f8-e7668ddd2249/NCRB_STATS.pdf
    [Google Scholar]
  24. United Nations, Department of Economic and Social Affairs, Population Division. (2022). World population prospects 2022: Summary of results. United Nations. Retrieved from https://population.un.org/wpp/
    [Google Scholar]
  25. United Nations Office on Drugs and Crime. (2020, June 25). UNODC World Drug Report 2020: Global drug use rising; while COVID-19 has far reaching impact on global drug markets. Retrieved from https://www.unodc.org/unodc/frontpage/2020/June/unodc-world-drug-report-2020_-global-drug-use-rising-while-covid-19-has-far-reaching-impact-on-global-drug-markets.html
    [Google Scholar]
  26. Singh, A. P., Seth, M., Bakshi, K., Uniyal, A. K., & Singh, H. (2023). JUVENILE JUSTICE IN INDIA–THE CHANGING FACE OF CRIMES BY YOUTH. Russian Law Journal, 11(5S), 156-161.
    [Google Scholar]
  27. Ministry of Law and Justice, Government of India. (2023). Annual reports. Department of Justice, Government of India. Retrieved from https://doj.gov.in/annual-reports/
    [Google Scholar]
  28. National Crime Records Bureau. (n.d.). National Crime Records Bureau (NCRB): Datasets. Data.gov.in. Retrieved October 25, 2025, from https://www.data.gov.in/ministrydepartment/National%20Crime%20Records%20Bureau%20(NCRB)
    [Google Scholar]
  29. Transparency International. (2022). Corruption perception index 2022. Retrieved from https://www.transparency.org/en/publications/corruption-perceptions-index-2022
    [Google Scholar]
  30. Central Vigilance Commission. (n.d.). Annual reports. Retrieved October 25, 2025, from https://www.cvc.gov.in/annualreport.html
    [Google Scholar]
  31. Vora, H. (2024). Police Brutality in India: Its Impact on Individuals and Their Rights. LawFoyer Int'l J. Doctrinal Legal Rsch., 2, 306.
    [Google Scholar]
  32. Institute for Crime & Justice Policy Research. (n.d.). World Prison Brief. Retrieved October 25, 2025, from https://www.prisonstudies.org/
    [Google Scholar]
  33. Bureau of Justice Statistics. (n.d.). Recidivism and reentry. Office of Justice Programs. Retrieved October 25, 2025, from https://bjs.ojp.gov/topics/recidivism-and-reentry
    [Google Scholar]
Cite This Article
APA Style
Pippal, S., & Ranga, A. (2026). Equilibria and Stability Analysis of a Compartmental Model for Crime Dynamics with Recidivism and Corruption. ICCK Journal of Applied Mathematics, 2(1), 1–43. https://doi.org/10.62762/JAM.2025.240326
Export Citation
RIS Format
Compatible with EndNote, Zotero, Mendeley, and other reference managers
RIS format data for reference managers
TY  - JOUR
AU  - Pippal, Sarita
AU  - Ranga, Ajay
PY  - 2026
DA  - 2026/01/15
TI  - Equilibria and Stability Analysis of a Compartmental Model for Crime Dynamics with Recidivism and Corruption
JO  - ICCK Journal of Applied Mathematics
T2  - ICCK Journal of Applied Mathematics
JF  - ICCK Journal of Applied Mathematics
VL  - 2
IS  - 1
SP  - 1
EP  - 43
DO  - 10.62762/JAM.2025.240326
UR  - https://www.icck.org/article/abs/JAM.2025.240326
KW  - dynamical systems
KW  - nonlinear system
KW  - differential equations
KW  - stability
KW  - bifurcation
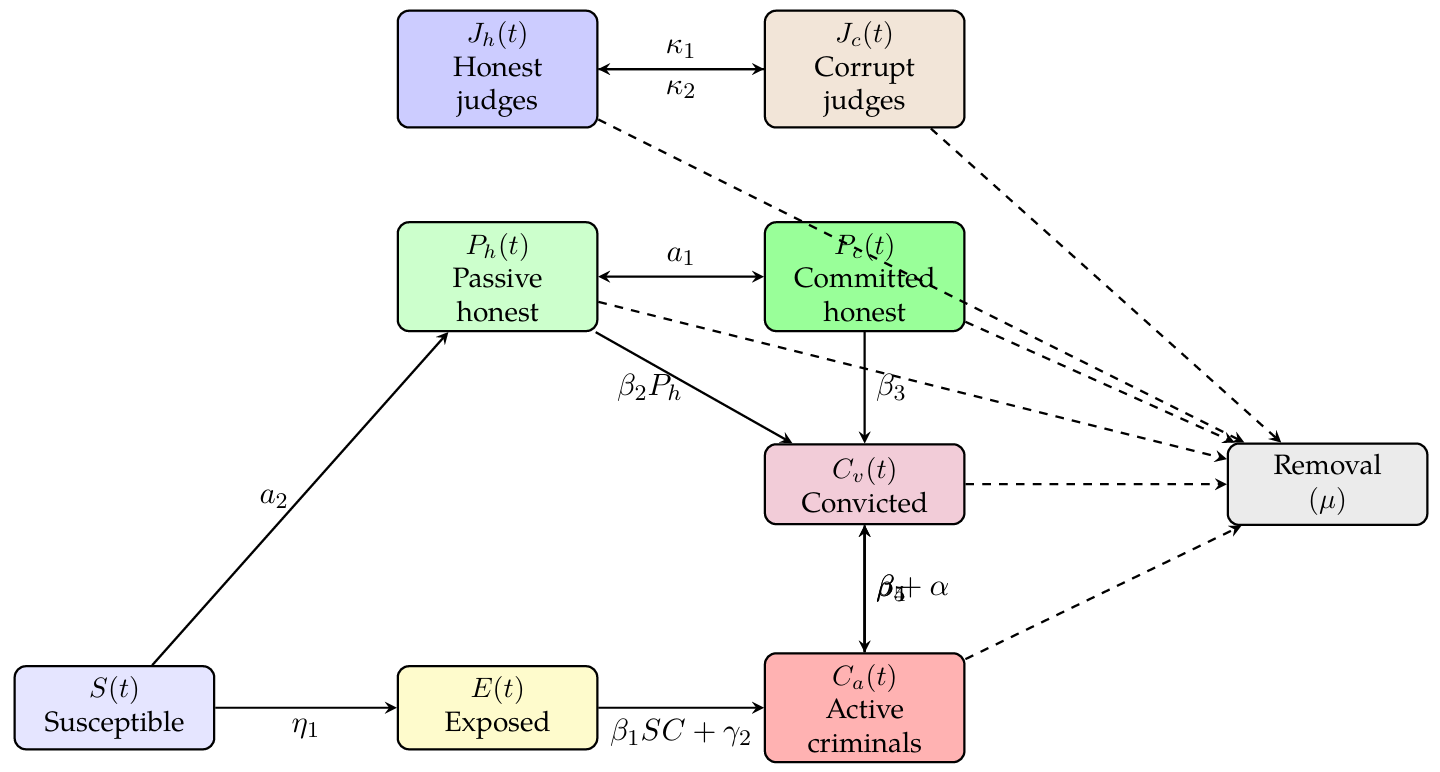
AB  - A nonlinear compartmental model is developed to analyze crime dynamics in a structured society. The population is stratified into eight compartments: \(S(t)\) (susceptible), \(E(t)\) (exposed), \(C(t)\) (active criminals), \(C_v(t)\) (convicted criminals), \(P_h(t)\) (passive-honest), \(P_c(t)\) (committed-honest), \(J_h(t)\) (honest judges), and \(J_c(t)\) (corrupt judges). The model incorporates nonlinear mechanisms such as institutional corruption (\(\kappa_1\)), judicial correction (\(\kappa_2\)), recidivism feedback (\(\rho_1,\rho_2\)), exposure intensity (\(\eta_1\)), and rehabilitation (\(r_2\)), providing a realistic portrayal of crime--justice interactions. Solutions remain positive and bounded within a feasible domain \(\mathcal{D}\). Linear stability analysis of the crime--free equilibrium \(Z_0\) is performed via the Jacobian \(J(Z_0)\). Numerical simulations explore the long--term dynamics under variations of key parameters (\(\beta_1,\eta_1,\rho_1,\rho_2,r_2,\kappa_1,\kappa_2\)). Results show that strong judicial recruitment (\(a_1\)) and honest reinforcement (\(\beta_4\)) suppress criminal activity, whereas increased corruption (\(\kappa_1\)) and recidivism (\(\rho_1,\rho_2\)) promote its growth. Bifurcation curves, contour maps, and stability basins highlight critical thresholds and equilibrium structures. The analysis demonstrates that proactive policy measures---reducing corruption, discouraging recidivism, and enhancing judicial integrity---can significantly lower crime levels and foster honest societal behavior, offering valuable guidance for designing effective crime--prevention strategies across diverse socio--political contexts.
SN  - 3068-5656
PB  - Institute of Central Computation and Knowledge
LA  - English
ER  -
BibTeX Format
Compatible with LaTeX, BibTeX, and other reference managers
BibTeX format data for LaTeX and reference managers
@article{Pippal2026Equilibria,
  author = {Sarita Pippal and Ajay Ranga},
  title = {Equilibria and Stability Analysis of a Compartmental Model for Crime Dynamics with Recidivism and Corruption},
  journal = {ICCK Journal of Applied Mathematics},
  year = {2026},
  volume = {2},
  number = {1},
  pages = {1-43},
  doi = {10.62762/JAM.2025.240326},
  url = {https://www.icck.org/article/abs/JAM.2025.240326},
  abstract = {A nonlinear compartmental model is developed to analyze crime dynamics in a structured society. The population is stratified into eight compartments: \(S(t)\) (susceptible), \(E(t)\) (exposed), \(C(t)\) (active criminals), \(C\_v(t)\) (convicted criminals), \(P\_h(t)\) (passive-honest), \(P\_c(t)\) (committed-honest), \(J\_h(t)\) (honest judges), and \(J\_c(t)\) (corrupt judges). The model incorporates nonlinear mechanisms such as institutional corruption (\(\kappa\_1\)), judicial correction (\(\kappa\_2\)), recidivism feedback (\(\rho\_1,\rho\_2\)), exposure intensity (\(\eta\_1\)), and rehabilitation (\(r\_2\)), providing a realistic portrayal of crime--justice interactions. Solutions remain positive and bounded within a feasible domain \(\mathcal{D}\). Linear stability analysis of the crime--free equilibrium \(Z\_0\) is performed via the Jacobian \(J(Z\_0)\). Numerical simulations explore the long--term dynamics under variations of key parameters (\(\beta\_1,\eta\_1,\rho\_1,\rho\_2,r\_2,\kappa\_1,\kappa\_2\)). Results show that strong judicial recruitment (\(a\_1\)) and honest reinforcement (\(\beta\_4\)) suppress criminal activity, whereas increased corruption (\(\kappa\_1\)) and recidivism (\(\rho\_1,\rho\_2\)) promote its growth. Bifurcation curves, contour maps, and stability basins highlight critical thresholds and equilibrium structures. The analysis demonstrates that proactive policy measures---reducing corruption, discouraging recidivism, and enhancing judicial integrity---can significantly lower crime levels and foster honest societal behavior, offering valuable guidance for designing effective crime--prevention strategies across diverse socio--political contexts.},
  keywords = {dynamical systems, nonlinear system, differential equations, stability, bifurcation},
  issn = {3068-5656},
  publisher = {Institute of Central Computation and Knowledge}
}
Article Metrics
Citations:

Google Scholar
0

Crossref

0

Scopus

0

Web of Science

0
Article Access Statistics:
Views: 139
PDF Downloads: 45
Publisher's Note
ICCK stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and Permissions
CC BY Copyright © 2026 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
ICCK Journal of Applied Mathematics

ICCK Journal of Applied Mathematics

ISSN: 3068-5656 (Online)

Email: [email protected]

Portico

Portico

All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/