Analysis of a Pest-Natural Enemy Model with Time Delay in Impulsive Releasing Natural Enemy

Hui Jiao; Sergey Meleshko

doi:10.62762/JMIA.2025.442174

Volume 1, Issue 1, Journal of Mathematics and Interdisciplinary Applications

Volume 1, Issue 1, 2025

Submit Manuscript Edit a Special Issue

Article QR Code

Scan the QR code for reading

Popular articles

Case Studies on Integrating Artificial Intelligence in Finance to Transform Decision Making and Risk Management for Enhanced Financial Outcomes Reservoir Science: A Multi-Coupling Communication Platform to Promote Energy Transformation, Climate Change and Environmental Protection Reinforcement Learning for Prompt Optimization in Language Models: A Comprehensive Survey of Methods, Representations, and Evaluation Challenges From CO$_2$ Sequestration to Hydrogen Storage: Further Utilization of Depleted Gas Reservoirs AI and the Future of Education: Advancing Personalized Learning and Intelligent Tutoring Systems Effects of Crosslinking Agents and Reservoir Conditions on the Propagation of Fractures in Coal Reservoirs During Hydraulic Fracturing The Influence of Geological Factors and Transmission Fluids on the Exploitation of Reservoir Geothermal Resources: Factor Discussion and Mechanism Analysis YOLOv8-Lite: A Lightweight Object Detection Model for Real-time Autonomous Driving Systems Plant Disease Detection Using Deep Learning Techniques Current Status and Development Prospects of Carbon Capture, Utilization, and Storage (CCUS) in China: Technical, Policy, and Market Perspectives

Journal of Mathematics and Interdisciplinary Applications, Volume 1, Issue 1, 2025: 20-28

Open Access | Research Article | 26 November 2025

Analysis of a Pest-Natural Enemy Model with Time Delay in Impulsive Releasing Natural Enemy

Hui Jiao 1 *

Sergey Meleshko 1

1 School of Mathematics, Institute of Science, Suranaree University of Technology, Nakhon, Ratchasima 30000, Thailand

* Corresponding Author: Hui Jiao, [email protected]

DOI: 10.62762/JMIA.2025.442174

ARK: ark:/57805/jmia.2025.442174

Received: 16 August 2025, Accepted: 01 September 2025, Published: 26 November 2025

PDF (6.73 MB)

Article Metrics Cite This Article

Abstract

Releasing amount of natural enemy generally depends on its population data, while impulsive releasing natural enemy usually brings about a time delay after the data is observed in the practical pest management. Therefore, it is very important for pest managers to assess the impact of the time delay in pest management. In this paper, we construct a pest-natural enemy model with time delay in impulsive releasing natural enemy. We prove that the pest-free periodic solution of model $(2.1)$ is globally attractive with $\eta \tau<\frac{\zeta y^{\ast}(1-e^{-\lambda \tau})}{\lambda}$. We also prove that model $(2.1)$ is permanent with $\eta \tau>\frac{\zeta y^{\ast}(1-e^{-\lambda \tau})}{\lambda}$. Further influence of the time delay in impulsive releasing on dynamical behaviors of model $(2.1)$ is investigated by numerical simulations. Our results provide reliable tactics for pest management.

Graphical Abstract

Keywords

pest-natural enemy model

time delay

impulsive releasing

pest management

pest-free

Data Availability Statement

Data will be made available on request.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grant 12261018; in part by the Universities Key Laboratory of System Modeling and Data Mining in Guizhou Province under Grant 2023013; in part by the Innovation Exploration and Academic New Seedling Project of Guizhou University of Finance and Economics under Grant 2024XSXMA08.

Conflicts of Interest

The authors declare no conflicts of interest.

Ethical Approval and Consent to Participate

Not applicable.

References

Mongillo, J. F., & Zierdt-Warshaw, L. (2000). Encyclopedia of environmental science. University Rochester Press.
[Google Scholar]
Lacey, L. A. (Ed.). (2016). Microbial control of insect and mite pests: from theory to practice. Academic Press.
[Google Scholar]
Amarathunga, D. C., Parry, H., Grundy, J., & Dorin, A. (2024). A predator–prey population dynamics simulation for biological control of Frankliniella occidentalis (Western Flower Thrips) by Orius laevigatus in strawberry plants. Biological Control, 188, 105409.
[CrossRef] [Google Scholar]
Barclay, H. J. (1987). Models for pest control: complementary effects of periodic releases of sterile pests and parasitoids. Theoretical Population Biology, 32(1), 76-89.
[CrossRef] [Google Scholar]
Liu, X., & Chen, L. (2003). Complex dynamics of Holling type II Lotka–Volterra predator–prey system with impulsive perturbations on the predator. Chaos, Solitons & Fractals, 16(2), 311-320.
[CrossRef] [Google Scholar]
Jiao, J., Chen, L., & Cai, S. (2009). A delayed stage-structured Holling II predator–prey model with mutual interference and impulsive perturbations on predator. Chaos, Solitons & Fractals, 40(4), 1946-1955.
[CrossRef] [Google Scholar]
Jiao, J., Chen, L., Cai, S., & Wang, L. (2010). Dynamics of a stage-structured predator–prey model with prey impulsively diffusing between two patches. Nonlinear Analysis: Real World Applications, 11(4), 2748-2756.
[CrossRef] [Google Scholar]
Wu, L., Jiao, J., & Dai, X. (2025). Dynamics of stage-structured ecological aquaculture management model with impulsive harvesting and nonlinearly releasing larval predators at different fixed moments. Journal of Computational Science, 85, 102532.
[CrossRef] [Google Scholar]
Pei, Y., Chen, L., Li, C., & Wang, C. (2006). Impulsive selective harvesting in a logistic fishery model with time delay. Journal of Biological Systems, 14(01), 91-99.
[CrossRef] [Google Scholar]
Lawson, J., & Braverman, E. (2023). Optimality and sustainability of delayed impulsive harvesting. Communications in Nonlinear Science and Numerical Simulation, 117, 106914.
[CrossRef] [Google Scholar]
Bainov, D., & Simeonov, P. (2017). Impulsive differential equations: periodic solutions and applications. Routledge.
[CrossRef] [Google Scholar]

Cite This Article

APA Style

Jiao, H., & Meleshko, S. (2025). Analysis of a Pest-Natural Enemy Model with Time Delay in Impulsive Releasing Natural Enemy. Journal of Mathematics and Interdisciplinary Applications, 1(1), 20–28. https://doi.org/10.62762/JMIA.2025.442174

Export Citation

RIS Format

Compatible with EndNote, Zotero, Mendeley, and other reference managers

RIS format data for reference managers

TY  - JOUR
AU  - Jiao, Hui
AU  - Meleshko, Sergey
PY  - 2025
DA  - 2025/11/26
TI  - Analysis of a Pest-Natural Enemy Model with Time Delay in Impulsive Releasing Natural Enemy
JO  - Journal of Mathematics and Interdisciplinary Applications
T2  - Journal of Mathematics and Interdisciplinary Applications
JF  - Journal of Mathematics and Interdisciplinary Applications
VL  - 1
IS  - 1
SP  - 20
EP  - 28
DO  - 10.62762/JMIA.2025.442174
UR  - https://www.icck.org/article/abs/JMIA.2025.442174
KW  - pest-natural enemy model
KW  - time delay
KW  - impulsive releasing
KW  - pest management
KW  - pest-free
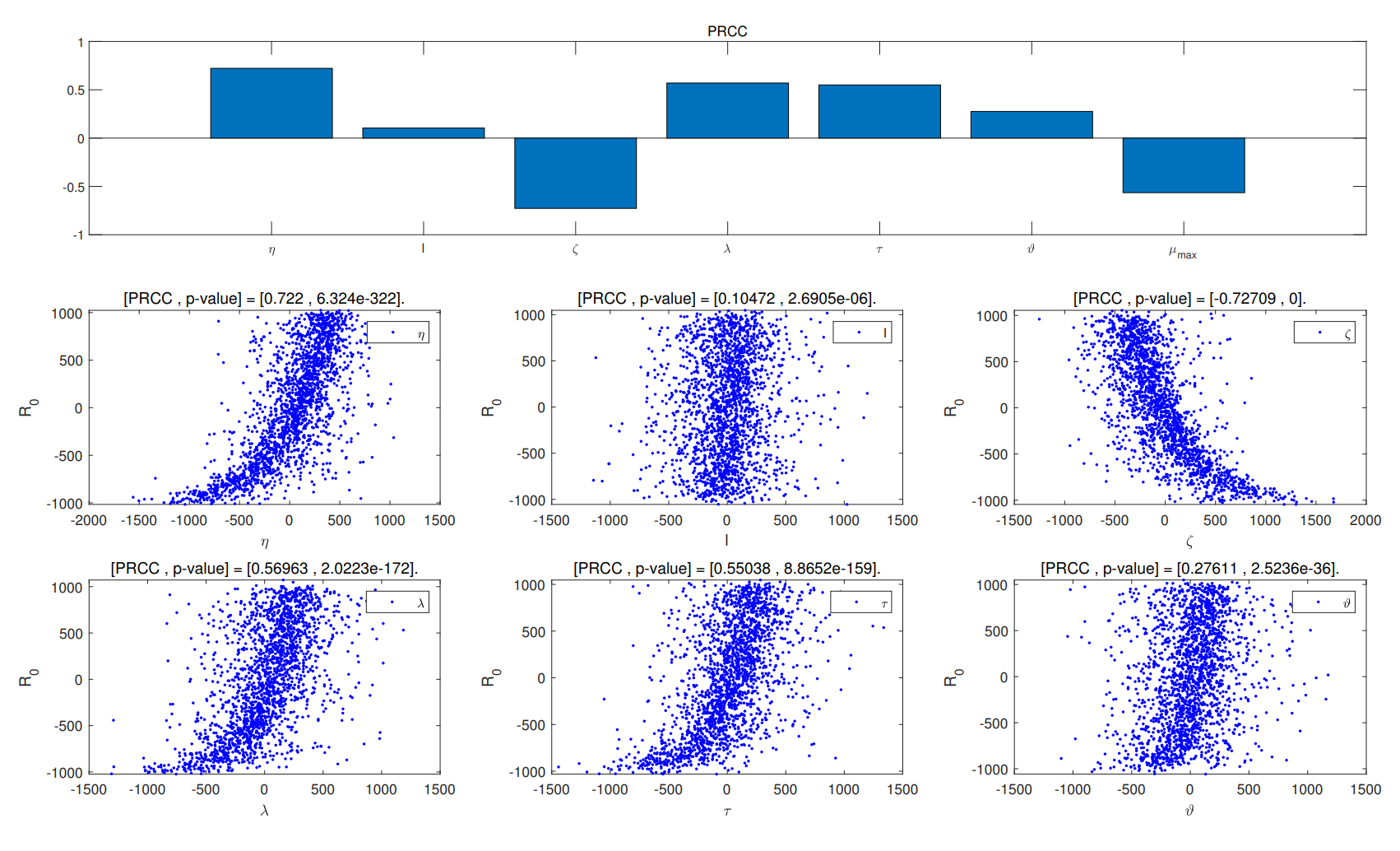
AB  - Releasing amount of natural enemy generally depends on its population data, while impulsive releasing natural enemy usually brings about a time delay after the data is observed in the practical pest management. Therefore, it is very important for pest managers to assess the impact of the time delay in pest management. In this paper, we construct a pest-natural enemy model with time delay in impulsive releasing natural enemy. We prove that the pest-free periodic solution of model $(2.1)$ is globally attractive with $\eta \tau\frac{\zeta y^{\ast}(1-e^{-\lambda \tau})}{\lambda}$. Further influence of the time delay in impulsive releasing on dynamical behaviors of model $(2.1)$ is investigated by numerical simulations. Our results provide reliable tactics for pest management.
SN  - 3070-393X
PB  - Institute of Central Computation and Knowledge
LA  - English
ER  -

BibTeX Format

Compatible with LaTeX, BibTeX, and other reference managers

BibTeX format data for LaTeX and reference managers

@article{Jiao2025Analysis,
  author = {Hui Jiao and Sergey Meleshko},
  title = {Analysis of a Pest-Natural Enemy Model with Time Delay in Impulsive Releasing Natural Enemy},
  journal = {Journal of Mathematics and Interdisciplinary Applications},
  year = {2025},
  volume = {1},
  number = {1},
  pages = {20-28},
  doi = {10.62762/JMIA.2025.442174},
  url = {https://www.icck.org/article/abs/JMIA.2025.442174},
  abstract = {Releasing amount of natural enemy generally depends on its population data, while impulsive releasing natural enemy usually brings about a time delay after the data is observed in the practical pest management. Therefore, it is very important for pest managers to assess the impact of the time delay in pest management. In this paper, we construct a pest-natural enemy model with time delay in impulsive releasing natural enemy. We prove that the pest-free periodic solution of model \$(2.1)\$ is globally attractive with \$\eta \tau\frac{\zeta y^{\ast}(1-e^{-\lambda \tau})}{\lambda}\$. Further influence of the time delay in impulsive releasing on dynamical behaviors of model \$(2.1)\$ is investigated by numerical simulations. Our results provide reliable tactics for pest management.},
  keywords = {pest-natural enemy model, time delay, impulsive releasing, pest management, pest-free},
  issn = {3070-393X},
  publisher = {Institute of Central Computation and Knowledge}
}

Article Metrics

Citations:

Google Scholar

Crossref

Scopus

Web of Science

Article Access Statistics:

PDF Downloads: 108

Publisher's Note

ICCK stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and Permissions

Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.

Journal of Mathematics and Interdisciplinary Applications

ISSN: 3070-393X (Online)

Email: [email protected]

Portico

All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/

User

Unlimited Downloads

Complete Library Access

Membership Eligibility

Community Leadership Opportunities

Google Scholar

Crossref

Scopus

Web of Science