Limit Cycles for Continuous Piecewise Linear Systems with Three Zones Having Two Degenerate Subsystems

Li Xiong; Kuilin Wu

doi:10.62762/JMIA.2025.453419

Volume 1, Issue 1, Journal of Mathematics and Interdisciplinary Applications

Volume 1, Issue 1, 2025

Submit Manuscript Edit a Special Issue

Article QR Code

Scan the QR code for reading

Popular articles

Case Studies on Integrating Artificial Intelligence in Finance to Transform Decision Making and Risk Management for Enhanced Financial Outcomes Reservoir Science: A Multi-Coupling Communication Platform to Promote Energy Transformation, Climate Change and Environmental Protection Reinforcement Learning for Prompt Optimization in Language Models: A Comprehensive Survey of Methods, Representations, and Evaluation Challenges From CO$_2$ Sequestration to Hydrogen Storage: Further Utilization of Depleted Gas Reservoirs AI and the Future of Education: Advancing Personalized Learning and Intelligent Tutoring Systems Effects of Crosslinking Agents and Reservoir Conditions on the Propagation of Fractures in Coal Reservoirs During Hydraulic Fracturing The Influence of Geological Factors and Transmission Fluids on the Exploitation of Reservoir Geothermal Resources: Factor Discussion and Mechanism Analysis YOLOv8-Lite: A Lightweight Object Detection Model for Real-time Autonomous Driving Systems Plant Disease Detection Using Deep Learning Techniques Current Status and Development Prospects of Carbon Capture, Utilization, and Storage (CCUS) in China: Technical, Policy, and Market Perspectives

Journal of Mathematics and Interdisciplinary Applications, Volume 1, Issue 1, 2025: 3-19

Open Access | Research Article | 05 November 2025

Limit Cycles for Continuous Piecewise Linear Systems with Three Zones Having Two Degenerate Subsystems

Li Xiong 1

Kuilin Wu 1 *

1 School of Mathematics and Statistics, Guizhou University, Guiyang 550025, China

* Corresponding Author: Kuilin Wu, [email protected]

DOI: 10.62762/JMIA.2025.453419

ARK: ark:/57805/jmia.2025.453419

Received: 24 August 2025, Accepted: 22 September 2025, Published: 05 November 2025

PDF (979.30 KB)

Article Metrics Cite This Article

Abstract

This paper deals with continuous piecewise linear differential systems with three zones separated by two parallel straight lines (for short, CPWL3). The number of limit cycles of CPWL3 systems with two degenerate subsystems is not clear. In the paper, we provide a complete study on the maximum number of limit cycles by geometric techniques when the continuous piecewise linear systems with three zones have two degenerate subsystems. During our analysis, we also detect some bifurcation phenomena, such as boundary equilibrium bifurcation, scabbard bifurcation, grazing bifurcation, heteroclinic bifurcation and Hopf bifurcation.

Graphical Abstract

Keywords

limit cycle

piecewise linear systems

bifurcation

Data Availability Statement

Data will be made available on request.

Funding

This work was supported by the Science and Technology Plan Project of Guizhou Province under Grant ZK[2022]G118.

Conflicts of Interest

The authors declare no conflicts of interest.

Ethical Approval and Consent to Participate

Not applicable.

References

Françoise, J. P., & Xiao, D. (2015). Perturbation theory of a symmetric center within Liénard equations. Journal of Differential Equations, 259(6), 2408-2429.
[CrossRef] [Google Scholar]
Yuan, Z., Ke, A., & Han, M. (2022). On the number of limit cycles of a class of Liénard–Rayleigh oscillators. Physica D: Nonlinear Phenomena, 438, 133366.
[CrossRef] [Google Scholar]
Chen, T., Li, S., & Llibre, J. (2020). Z2-equivariant linear type bi-center cubic polynomial Hamiltonian vector fields. Journal of differential equations, 269(1), 832-861.
[CrossRef] [Google Scholar]
Li, F., Liu, Y., Liu, Y., & Yu, P. (2018). Bi-center problem and bifurcation of limit cycles from nilpotent singular points in Z2-equivariant cubic vector fields. Journal of Differential Equations, 265(10), 4965-4992.
[CrossRef] [Google Scholar]
Wei, L., & Zhang, X. (2020). Limit cycles bifurcating from periodic orbits near a centre and a homoclinic loop with a nilpotent singularity of Hamiltonian systems. Nonlinearity, 33(6), 2723.
[CrossRef] [Google Scholar]
Xiong, Y., Han, M., & Xiao, D. (2021). The maximal number of limit cycles bifurcating from a Hamiltonian triangle in quadratic systems. Journal of Differential Equations, 280, 139-178.
[Google Scholar]
Filippov, A. F. (1988). Differential equations with discontinuous righthand sides: Control systems. Dordrecht, Netherlands: Kluwer Academic Publishers.
[Google Scholar]
Bernardo, M., Budd, C., Champneys, A. R., & Kowalczyk, P. (2008). Piecewise-smooth dynamical systems: theory and applications (Vol. 163). Springer Science & Business Media.
[Google Scholar]
Freire, E., Ponce, E., Rodrigo, F., & Torres, F. (1998). Bifurcation sets of continuous piecewise linear systems with two zones. International Journal of Bifurcation and Chaos, 8(11), 2073-2097.
[CrossRef] [Google Scholar]
Han, M., & Zhang, W. (2010). On Hopf bifurcation in non-smooth planar systems. Journal of Differential Equations, 248(9), 2399-2416.
[CrossRef] [Google Scholar]
Freire, E., Ponce, E., & Torres, F. (2012). Canonical discontinuous planar piecewise linear systems. SIAM Journal on Applied Dynamical Systems, 11(1), 181-211.
[CrossRef] [Google Scholar]
Llibre, J. (2019). Limit cycles in continuous and discontinuous piecewise linear differential systems with two pieces separated by a straight line. Buletinul Academiei de Ştiinţe a Republicii Moldova. Matematica, 90(2), 3-12.
[Google Scholar]
Wang, J., Huang, C., & Huang, L. (2019). Discontinuity-induced limit cycles in a general planar piecewise linear system of saddle–focus type. Nonlinear Analysis: Hybrid Systems, 33, 162-178.
[CrossRef] [Google Scholar]
Huan, S. M., & Yang, X. S. (2013). Existence of limit cycles in general planar piecewise linear systems of saddle–saddle dynamics. Nonlinear Analysis: Theory, Methods & Applications, 92, 82-95.
[CrossRef] [Google Scholar]
Medrado, J. C., & Torregrosa, J. (2015). Uniqueness of limit cycles for sewing planar piecewise linear systems. Journal of Mathematical Analysis and Applications, 431(1), 529-544.
[CrossRef] [Google Scholar]
Li, T. (2019). Limit cycles and bifurcations in a class of discontinuous piecewise linear systems. International Journal of Bifurcation and Chaos, 29(10), 1950135.
[CrossRef] [Google Scholar]
Carmona, V., Fernandez-Sanchez, F., & Novaes, D. D. (2023). Uniform upper bound for the number of limit cycles of planar piecewise linear differential systems with two zones separated by a straight line. Applied Mathematics Letters, 137, 108501.
[CrossRef] [Google Scholar]
Chen, L., & Liu, C. (2024). The discontinuous planar piecewise linear systems with two improper nodes have at most one limit cycle. Nonlinear Analysis: Real World Applications, 80, 104180.
[CrossRef] [Google Scholar]
Liang, F., Romanovski, V. G., & Zhang, D. (2018). Limit cycles in small perturbations of a planar piecewise linear Hamiltonian system with a non-regular separation line. Chaos, Solitons & Fractals, 111, 18-34.
[CrossRef] [Google Scholar]
Sun, L., & Du, Z. (2024). Crossing Limit Cycles in Planar Piecewise Linear Systems Separated by a Nonregular Line with Node–Node Type Critical Points. International Journal of Bifurcation and Chaos, 34(04), 2450049.
[CrossRef] [Google Scholar]
Zhao, Q., & Yu, J. (2019). Poincaré Maps of “<”-Shape Planar Piecewise Linear Dynamical Systems with a Saddle. International Journal of Bifurcation and Chaos, 29(12), 1950165.
[CrossRef] [Google Scholar]
Alves, A. M., & Euzébio, R. D. (2023). Periodic trajectories in planar discontinuous piecewise linear systems with only centers and with a nonregular switching line. Nonlinearity, 36(12), 6747.
[CrossRef] [Google Scholar]
Wei, Z., Cheng, X., Duan, J., Moroz, I., & Zhang, L. (2025). Limit cycles in planar piecewise linear systems of saddle-saddle type with a nonregular separation line. Discrete and Continuous Dynamical Systems-Series B.
[CrossRef] [Google Scholar]
Braga, D. D. C., & Mello, L. F. (2014). More than three limit cycles in discontinuous piecewise linear differential systems with two zones in the plane. International Journal of Bifurcation and Chaos, 24(04), 1450056.
[CrossRef] [Google Scholar]
Zou, C., & Yang, J. (2018). Piecewise linear differential system with a center-saddle type singularity. Journal of Mathematical Analysis and Applications, 459(1), 453-463.
[CrossRef] [Google Scholar]
Gasull, A. (2021). Some open problems in low dimensional dynamical systems. SeMA Journal, 78(3), 233-269.
[CrossRef] [Google Scholar]
Andrade, K. D. S., Cespedes, O. A., Cruz, D. R., & Novaes, D. D. (2021). Higher order Melnikov analysis for planar piecewise linear vector fields with nonlinear switching curve. Journal of differential equations, 287, 1-36.
[CrossRef] [Google Scholar]
Berbache, A., & Tababouchet, I. (2024). Four crossing limit cycles of a family of discontinuous piecewise linear systems with three zones separated by two parallel straight lines. Boletín de la Sociedad Matemática Mexicana, 30(2), 50.
[CrossRef] [Google Scholar]
Liu, S., & Zhang, T. (2025). Limit Cycles and Stability Analysis in 3-Piecewise Linear Differential Systems with a Double Heteroclinic Loop. International Journal of Bifurcation and Chaos, 2550179.
[CrossRef] [Google Scholar]
Li, Z., & Liu, X. (2021). Limit cycles in the discontinuous planar piecewise linear systems with three zones. Qualitative theory of dynamical systems, 20(3), 79.
[CrossRef] [Google Scholar]
Xiong, Y., & Wang, C. (2021). Limit cycle bifurcations of planar piecewise differential systems with three zones. Nonlinear Analysis: Real World Applications, 61, 103333.
[CrossRef] [Google Scholar]
Chen, H., Wei, F., Xia, Y. H., & Xiao, D. (2020). Global dynamics of an asymmetry piecewise linear differential system: Theory and applications. Bulletin des Sciences Mathématiques, 160, 102858.
[CrossRef] [Google Scholar]
Euzebio, R., Pazim, R., & Ponce, E. (2016). Jump bifurcations in some degenerate planar piecewise linear differential systems with three zones. Physica D: Nonlinear Phenomena, 325, 74-85.
[CrossRef] [Google Scholar]
Chen, H., Jia, M., & Tang, Y. (2021). A degenerate planar piecewise linear differential system with three zones. Journal of Differential Equations, 297, 433-468.
[CrossRef] [Google Scholar]
Ponce, E., Ros, J., & Vela, E. (2015). Limit cycle and boundary equilibrium bifurcations in continuous planar piecewise linear systems. International Journal of Bifurcation and Chaos, 25(03), 1530008.
[CrossRef] [Google Scholar]
Lima, M. F. S., Pessoa, C., & Pereira, W. F. (2017). Limit cycles bifurcating from a period annulus in continuous piecewise linear differential systems with three zones. International Journal of Bifurcation and Chaos, 27(02), 1750022.
[CrossRef] [Google Scholar]
Freire, E., Ponce, E., Rodrigo, F., & Torres, F. (2002). Bifurcation sets of symmetrical continuous piecewise linear systems with three zones. International Journal of Bifurcation and Chaos, 12(08), 1675-1702.
[CrossRef] [Google Scholar]
Zhang, Z. (1992). Qualitative theory of differential equations (Vol. 101). American Mathematical Soc..
[Google Scholar]
Xiong, L., Wu, K., & Li, S. (2023). Global dynamics of a degenerate planar piecewise linear differential system with three zones. Bulletin des Sciences Mathématiques, 184, 103258.
[CrossRef] [Google Scholar]

Cite This Article

APA Style

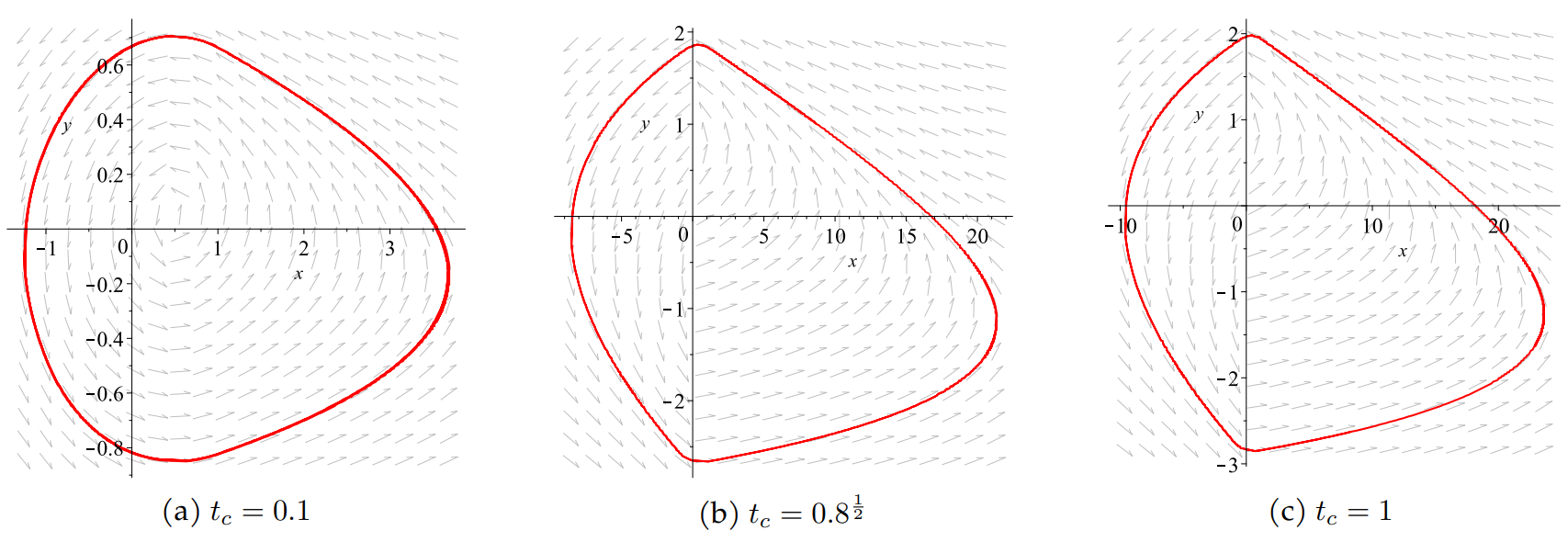
Xiong, L., & Wu, K. (2025). Limit Cycles for Continuous Piecewise Linear Systems with Three Zones Having Two Degenerate Subsystems. Journal of Mathematics and Interdisciplinary Applications, 1(1), 3–19. https://doi.org/10.62762/JMIA.2025.453419

Export Citation

RIS Format

Compatible with EndNote, Zotero, Mendeley, and other reference managers

RIS format data for reference managers

TY  - JOUR
AU  - Xiong, Li
AU  - Wu, Kuilin
PY  - 2025
DA  - 2025/11/05
TI  - Limit Cycles for Continuous Piecewise Linear Systems with Three Zones Having Two Degenerate Subsystems
JO  - Journal of Mathematics and Interdisciplinary Applications
T2  - Journal of Mathematics and Interdisciplinary Applications
JF  - Journal of Mathematics and Interdisciplinary Applications
VL  - 1
IS  - 1
SP  - 3
EP  - 19
DO  - 10.62762/JMIA.2025.453419
UR  - https://www.icck.org/article/abs/JMIA.2025.453419
KW  - limit cycle
KW  - piecewise linear systems
KW  - bifurcation
AB  - This paper deals with continuous piecewise linear differential systems with three zones separated by two parallel straight lines (for short, CPWL3). The number of limit cycles of CPWL3 systems with two degenerate subsystems is not clear. In the paper, we provide a complete study on the maximum number of limit cycles by geometric techniques when the continuous piecewise linear systems with three zones have two degenerate subsystems. During our analysis, we also detect some bifurcation phenomena, such as boundary equilibrium bifurcation, scabbard bifurcation, grazing bifurcation, heteroclinic bifurcation and Hopf bifurcation.
SN  - 3070-393X
PB  - Institute of Central Computation and Knowledge
LA  - English
ER  -

BibTeX Format

Compatible with LaTeX, BibTeX, and other reference managers

BibTeX format data for LaTeX and reference managers

@article{Xiong2025Limit,
  author = {Li Xiong and Kuilin Wu},
  title = {Limit Cycles for Continuous Piecewise Linear Systems with Three Zones Having Two Degenerate Subsystems},
  journal = {Journal of Mathematics and Interdisciplinary Applications},
  year = {2025},
  volume = {1},
  number = {1},
  pages = {3-19},
  doi = {10.62762/JMIA.2025.453419},
  url = {https://www.icck.org/article/abs/JMIA.2025.453419},
  abstract = {This paper deals with continuous piecewise linear differential systems with three zones separated by two parallel straight lines (for short, CPWL3). The number of limit cycles of CPWL3 systems with two degenerate subsystems is not clear. In the paper, we provide a complete study on the maximum number of limit cycles by geometric techniques when the continuous piecewise linear systems with three zones have two degenerate subsystems. During our analysis, we also detect some bifurcation phenomena, such as boundary equilibrium bifurcation, scabbard bifurcation, grazing bifurcation, heteroclinic bifurcation and Hopf bifurcation.},
  keywords = {limit cycle, piecewise linear systems, bifurcation},
  issn = {3070-393X},
  publisher = {Institute of Central Computation and Knowledge}
}

Article Metrics

Citations:

Google Scholar

Crossref

Scopus

Web of Science

Article Access Statistics:

PDF Downloads: 289

Publisher's Note

ICCK stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and Permissions

Copyright © 2025 by the Author(s). Published by Institute of Central Computation and Knowledge. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.

Journal of Mathematics and Interdisciplinary Applications

ISSN: 3070-393X (Online)

Email: [email protected]

Portico

All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/

User

Unlimited Downloads

Complete Library Access

Membership Eligibility

Community Leadership Opportunities

Google Scholar

Crossref

Scopus

Web of Science