ICCK Transactions on Systems Safety and Reliability
ISSN: 3069-1087 (Online)
Email: [email protected]
 Submit Manuscript
Edit a Special Issue
Submit Manuscript
Edit a Special Issue
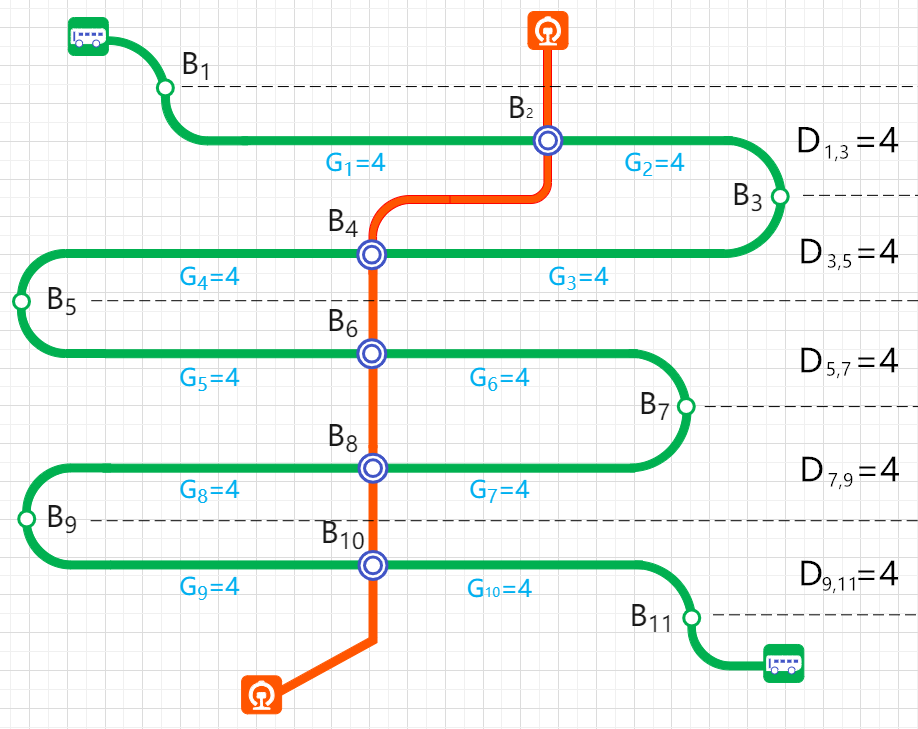
TY - JOUR AU - Gao, Kaiye AU - Yu, Rongquan AU - Zhang, Sicheng AU - Wu, Di PY - 2026 DA - 2026/01/29 TI - Reliability of Coupled Subway and Bus Networks under Uncertainty JO - ICCK Transactions on Systems Safety and Reliability T2 - ICCK Transactions on Systems Safety and Reliability JF - ICCK Transactions on Systems Safety and Reliability VL - 2 IS - 1 SP - 3 EP - 10 DO - 10.62762/TSSR.2025.612115 UR - https://www.icck.org/article/abs/TSSR.2025.612115 KW - reliability KW - coupled subway and bus system KW - demand uncertainty KW - capacity constraints KW - subway priority behavior AB - In urban public transport networks, subway and bus systems complement each other and together form a coupled system that serves passenger travel. However, a disturbance in either subsystem can propagate through coupling nodes across the entire network, thereby reducing overall operational efficiency. Most existing studies focus only on the reliability of a single mode, and few have analyzed the overall reliability of the system while considering the coupling relationship between the two. To address this gap, this paper proposes a probabilistic evaluation model to assess the reliability of the subway and bus coupling system. System reliability is defined as the probability that the network can meet all passenger demand given uncertain demand and limited road and rail capacity. The model accounts for passengers’ travel behavior of “prioritizing the subway” and, by sequentially computing the load on each road section, the subway’s share, and the remaining bus load, determines whether the system is reliable under a given demand combination. This provides an effective quantitative tool for the planning and optimization of integrated urban transportation systems. SN - 3069-1087 PB - Institute of Central Computation and Knowledge LA - English ER -
@article{Gao2026Reliabilit,
author = {Kaiye Gao and Rongquan Yu and Sicheng Zhang and Di Wu},
title = {Reliability of Coupled Subway and Bus Networks under Uncertainty},
journal = {ICCK Transactions on Systems Safety and Reliability},
year = {2026},
volume = {2},
number = {1},
pages = {3-10},
doi = {10.62762/TSSR.2025.612115},
url = {https://www.icck.org/article/abs/TSSR.2025.612115},
abstract = {In urban public transport networks, subway and bus systems complement each other and together form a coupled system that serves passenger travel. However, a disturbance in either subsystem can propagate through coupling nodes across the entire network, thereby reducing overall operational efficiency. Most existing studies focus only on the reliability of a single mode, and few have analyzed the overall reliability of the system while considering the coupling relationship between the two. To address this gap, this paper proposes a probabilistic evaluation model to assess the reliability of the subway and bus coupling system. System reliability is defined as the probability that the network can meet all passenger demand given uncertain demand and limited road and rail capacity. The model accounts for passengers’ travel behavior of “prioritizing the subway” and, by sequentially computing the load on each road section, the subway’s share, and the remaining bus load, determines whether the system is reliable under a given demand combination. This provides an effective quantitative tool for the planning and optimization of integrated urban transportation systems.},
keywords = {reliability, coupled subway and bus system, demand uncertainty, capacity constraints, subway priority behavior},
issn = {3069-1087},
publisher = {Institute of Central Computation and Knowledge}
}
ICCK Transactions on Systems Safety and Reliability
ISSN: 3069-1087 (Online)
Email: [email protected]

Portico
All published articles are preserved here permanently:
https://www.portico.org/publishers/icck/