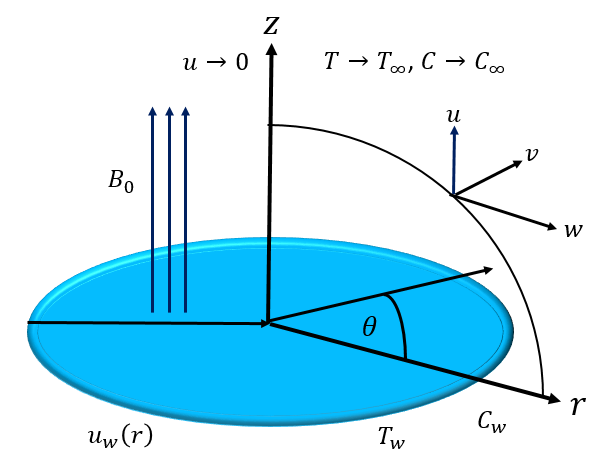
This study investigates the magnetohydrodynamic (MHD) flow of Boger tri-hybrid nanofluid (tri-HNF) through a stretching disk. A novel machine learning technique, specifically the Levenberg--Marquardt (LM) scheme under a backpropagated artificial neural network (ANN), is used to predict the flow dynamics with heat and mass transfer. The Cattaneo-Christov mass and heat fluxes model, permeable media, and viscous dissipation are considered. The well-known Brinkman-Hamilton and Crosser model is used to describe thermal conductivity and viscosity models. The computational solution to the current problem has been obtained using the Bvp4c approach, which is based on finite differences. In order to examine the numerical solutions and anticipated outcomes, LM-BNN uses a numerical dataset that is split into three categories: 15% for testing, 70% for training, and 15% for validation. Regression analysis, surface stresses, error histogram, correlation index, heat and mass transfer, and mean squared error-based fitness curves, which range from $10^{- 10}$ to $10^{- 8}$ are used to validate the consistency and efficacy of LM-BNN. The findings suggest that the velocity profile declines with the magnetic and relaxation time ratio parameter. The temperature and concentration decrease with thermal and solutal relaxation parameters. The heat and mass transfer rates are significant for solvent viscosity and nanomaterials load.